Численные методы 1. Метод начальных параметров
Краткие теоретические сведения
В методе начальных параметров краевую задачу для системы дифференциальных уравнений пытаются заменить задачей Коши. При этом предполагается, что в распоряжении расчётчика имеется программное обеспечение для решения начальной задачи для нормальной системы дифференциальных уравнений.
Рассмотрим метод начальных параметров для решения нормальной системы n дифференциальных уравнений 1-го порядка
. (11.1)
Если эта система дополнена начальными условиями y (x 1)= y 1, то её можно решить с помощью стандартного программного обеспечения, например, методов Рунге-Кутта. Рассмотрим случай, когда эта система дополнена граничными условиями: часть координат вектора y задана на левом конце x 1, а часть – на правом x 2. Пусть, для определённости, на правом конце заданы m первых координат вектора y, а на левом конце – n - m последних. Этого всегда можно добиться перенумерацией переменных. Если бы нам удалось найти недостающие координаты y на левом конце, то можно было бы решить начальную задачу. Будем рассматривать m недостающих координат y в начальной точке x 1 как неизвестные t 1, t 2,…, tm. Для их нахождения имеется m уравнений – граничные условия на правом конце x 2. Таким образом, задача нахождения неизвестных начальных условий сводится к решению системы из m в общем случае нелинейных уравнений.
Рис. 11.1. Геометрическая интерпретация метода начальных параметров
Если n =2, а m =1, то геометрическая интерпретация метода начальных параметров показана на рис.11.1. Задавая различные значения для недостающего начального условия y ¢(x 1), будем получать различные y (x 2). Чтобы получить нужное значение y 2, нужно угадать угол наклона экстремали в начальной точке. Это напоминает процесс стрельбы из артиллерийского орудия. Поэтому метод начальных параметров называется также методом стрельбы.
Если исходная система дифференциальных уравнений (11.1) линейная (даже с переменными коэффициентами), то вектор решений в любой точке y (x 2) также будет линейно зависеть от начальных условий:
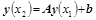. (11.2)
Оставим в системе (11.2) только m первых строк, соответствующих граничным условиям при x = x 2, и только m первых столбцов, соответствующих неизвестным начальным параметрам:
(11.3)
Для нахождения компонентов матрицы A и координат вектора b нужно решить начальную задачу m +1 раз с такими вариантами неизвестных начальных условий:
t ={1,0,…,0} – для формирования { a 11+ b 1, a 21+ b 2,…, am 1+ bm };
t ={0,1,…,0} – для формирования { a 12+ b 1, a 22+ b 2,…, am 2+ bm };
…
t ={0,0,…,1} – для формирования { a 1 m + b 1, a 2 m + b 2,…, amm + bm };
а также
t ={0,0,…,0} – для формирования { b 1, b 2,…, bm }.
Поэтому метод начальных параметров называют также методом матричной прогонки.
Если n =2, а m =1, то геометрическая интерпретация метода начальных параметров показана на рис.11.1. Задавая различные значения для недостающего начального условия y ¢(x 1), будем получать различные y (x 2). Чтобы получить нужное значение y 2, нужно угадать угол наклона экстремали в начальной точке. Это напоминает процесс стрельбы из артиллерийского орудия. Поэтому метод начальных параметров называется также методом стрельбы.
