Прямолинейно-параллельный поток
Нелинейный степенной закон фильтрации в данном случае принимает вид:
(3.1)
Определим дебит и распределение давления.
Для определения постоянного дебита Q разделим переменные в формуле (3.1) и проинтегрируем в пределах от Рк до Рг и от 0 до Lк:
,
откуда
. (3.2)
Интегрируя выражение (3.1) в пределах от Рк до Р и от 0 до x, найдем распределение давления:
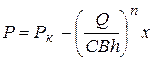
или, с учетом выражения (3.2):
. (3.3)
Таким образом, распределение давления при нелинейном законе фильтрации (3.1) совпадает с формулой распределения давления в аналогичном потоке при фильтрации по закону Дарси.
Скорость фильтрации равна:
. (3.4)
Скорость фильтрации постоянна во всем фильтрационном потоке.
Плоскорадиальный поток
Степенной закон фильтрации в данном случае принимает вид:
(3.5)
Отсюда
Разделив переменные и проинтегрировав в пределах от Рс до Рк и от Rc до Rk, получим:
(3.6)
В предельном случае при n=2 (закон Краснопольского) из уравнения (3.6) имеем:
.
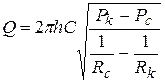Пренебрегая величиной 
по сравнению с 
, получим:
. (3.7)
Интегрируя выражение (3.5) в переделах от Рк до Р и от Rk до r, найдем распределение давления в потоке:
. (3.8)
При n=2
. (3.9)
Rак видно из формулы (3.6), индикаторная линия при 1£n£2 будет иметь вид выпуклой к оси дебитов степенной кривой с дробным показателем степени. В случае выполнения закона Краснопольского индикаторная линия является параболой второго порядка.
Кривая распределения давления в плоскорадиальном потоке при нелинейном законе фильтрации, как видно из формулы (3.8), имеет форму гиперболы. Воронка депрессии является гиперболоидом вращения, и ее крутизна у стенки скважины будет больше, чем у логарифмической кривой.
В реальных условиях при небольших дебитах скважины фильтрация может происходить по линейному закону. С увеличением дебита вблизи забоя скважины начинается нарушение линейного закона фильтрации. По мере увеличения дебита область потока, в которой нарушен закон Дарси, будет расширяться. В этих случаях удобно использовать двучленный закон фильтрации:
, (3.10)
где 
.
Выражая скорость фильтрации V через дебит Q
,
разделяя переменные и интегрируя в соответствующих пределах, находим:
а) распределение давления в пласте:
;
б) дебит скважины
.
Дебит Q находится как положительный корень квадратного уравнения, из которого видно, что индикаторная линия в этом случае является параболой.
Контрольные вопросы:
1. Охарактеризуйте типы одномерных фильтрационных потоков.
2. Проанализируйте расчетные зависимости для определения характеристик прямолинейно-параллельного потока.
3. Проанализируйте расчетные зависимости для определения характеристик плоскорадиального потока.
4. Дайте определение коэффициента продуктивности скважины.
5. Охарактеризуйте основные виды макронеоднородности пластов.
6. Сравните и проанализируйте основные характеристики фильтрационных потоков в слоисто-неоднородном и зонально-неоднородном пластах.
7. Постройте схемы распределения давления в плоскорадиальном потоке жидкости для слоисто-неоднородного и зонально-неоднородного пластов.
8. Сопоставьте выражения для определения дебита и давления в случаях соблюдения и нарушения закона Дарси. Отдельно рассмотрите прямолинейно-параллельный и плоскорадиальный потоки.
