Контрольная работа состоит из 2 частей: теоретического вопроса и двух задач. Формулировка условий задач одинакова для всех вариантов. Числовые данные для решения задач – различны, указаны ниже по вариантам в соответствующих таблицах. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.
Контрольная работа оформляется в тетради с указанием варианта, условий заданий и решения. Сначала излагается ответ на теоретический вопрос, а затем решение задач. Решение задач следует излагать подробно, объясняя все выполненные действия и используемые формулы. В конце работы привести список использованной литературы. Титульный лист оформить в соответствии с требованиями, принятыми в ТюмГУ. (на обложке тетради должен быть наклеен титульный лист (компьютерный текст) с указанием названия учебного заведения, направления, названия предмета, номера варианта работы, ФИО студента и преподавателя).
Контрольная работа должна быть сдана на проверку в процессе изучения дисциплины до сдачи экзамена. К экзамену студент допускается только после приема контрольной работы преподавателем.
1. Теоретические вопросы:
0. Аддитивная модель тренда и сезонных колебаний с применением фиктивных переменных.
1. Модели распределенных лагов: полиномиальная и геометрическая.
2. Двухшаговый метод наименьших квадратов.
3. Инструментальные переменные в регрессионном анализе. Тест Хаусмана.
4. Косвенный метод наименьших квадратов.
5. Модели бинарного выбора. Особенности оценивания параметров в логит- и пробит-моделях.
6. Понятие и обзор моделей Бокса–Дженкинса (AR, AM, ARMA, ARIMA).
7. Производственная функция Кобба-Дугласа, оценка параметров.
8. Обнаружение гетероскедастичности (тесты Парка, Спирмена).
9. Устранение (смягчение) гетероскедастичности. Метод взвешенных наименьших квадратов.
2. Задачи:
Задание № 1.
Имеются статистические данные (приложение №1) по некоторым регионам Российской Федерации. Для факторной переменной Х (численность населения) и результативной переменной Y (столбец N, где N – номер варианта) требуется:
1. Построить уравнение парной регрессии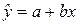 
, используя метод наименьших квадратов.
2. Оценить тесноту связи между переменными с помощью показателей корреляции и детерминации.
3. Охарактеризовать статистическую надежность результатов регрессионного анализа с использованием F-критерия Фишера при уровне значимости α = 0,05.
4. Оценить значимость коэффициентов регрессии и корреляции по t-критерию Стьюдента при уровне значимости α = 0,05.
5. Оцените при помощи средней ошибки аппроксимации качество уравнения.
6. Рассчитайте значение статистики DW (Дарбина-Уотсона) и сделайте вывод о наличии автокорреляции в ряду остатков.
7. Рассчитайте прогнозное значение результата, если значение фактора увеличится на 10 % от его среднего уровня.
Задание № 2.
По 20 предприятиям региона (приложение №2) изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов x1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x2 (%) (смотри таблицу своего варианта). Требуется:
1. Построить линейную модель множественной регрессии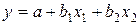 
.
2. Оценить статистическую значимость параметров регрессии с помощью t-критерия Стьюдента.
3. Найти коэффициенты множественной корреляции, множественной детерминации.
4. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
5. С помощью F -критерия Фишера оценить статистическую надежность уравнения регрессии
6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Приложение 1
