Далее приведены таблицы с основными свойствами пяти законов распределения случайной величины:
дискретные случайные величины
| Название распределения | Пара-метры | Закон распределения | MX | DX |
| Биномиальное | 
| 
| 
| 
|
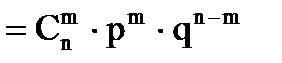
| Пуассона | 
| 
|
|
|
непрерывные случайные величины
| Название распределения | Пара-метры | Закон распределения | MX | DX |
| Равномерное на отрезке | 
| 
| 
| 
|
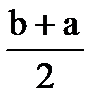
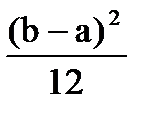
| Экспоненциальное | 
| 
| 
| 
|
| Нормальное | 
| 
| 
| 
|
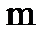
Примечания.
1. q=1-p
2. В таблице приведены для непрерывных величин выражения для плотностей распределения. Естественно, закон распределения можно также задать выражением для функции распределения.
Некоторые предельные теоремы теории вероятностей.
Локальная теорема Муавра – Лапласа.
Если 
, где n – количество независимых одинаковых опытов, в каждом из которых вероятность благоприятного исхода равна p, то закон распределения случайной величины – количества 
благоприятных исходов m в серии из n опытов сходится по вероятности к плотности нормального распределения
.
Интегральная теорема Муавра – Лапласа.
Если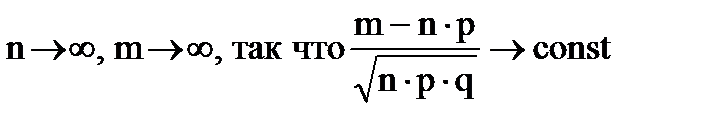 
, где n – количество независимых одинаковых опытов, в каждом из которых вероятность благоприятного исхода равна p, то функция распределения случайной величины – количества благоприятных исходов m в серии из n опытов сходится по вероятности к функции нормального распределения:
.
Теорема Пуассона.
Если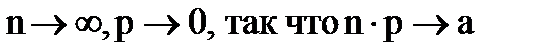 
, то вероятность того, что количество благоприятных исходов равно m, по вероятности сходится к величине, определяемой по формуле Пуассона:
.
При выполнении задания 2 предполагается использование встроенных функций системы Mathcad, таких как плотность распределения и функция распределения вероятностей для перечисленных выше законов. Обращение к этим функциям производится по имени. Имена и набор аргументов приведены в таблице:
| Распределение | Плотность распределения | Функция распределения |
| биномиальное | dbinom(m,n,p) | |
| Пуассона | dpois(m,a) | |
| равномерное | dunif(x,a,b) | punif(x,a,b) |
| экспоненциальное | dexp(x,λ) | pexp(x,λ) |
| нормальное | dnorm(x,m,σ) | pnorm(x,m,σ) |
Для того, чтобы обраться к одной из приведенных функций, необходимо выбрать кнопку f(x) на панели инструментов. В появившемся окне Insert Function выбрать категорию Probability Density (плотность вероятностей) или Probability Distribution (функция распределения), а затем имя функции.
Задание 2.
Каждый вариант второго задания состоит из двух пунктов:
2.1. Изучение пяти законов распределения;
2.2. Решение задачи с помощью одного из пяти законов распределения.
Задание 2.1.
Величина распределена по биномиальному закону. Постройте в одной системе координат многоугольники распределения для серии из n = N+5 (N - номер варианта) независимых испытаний с вероятностью успеха p = 0,1; 0,5; 0,9. Как изменяются вероятности при изменении р? Найдите математическое ожидание МХ и дисперсию DX случайной величины при заданных параметрах распределения.
Величина распределена по закону Пуассона. Постройте в одной системе координат многоугольники распределения при значениях параметра распределения а = N/10; N/5; N/2. Как изменяются вероятности при изменении величины а? Найдите математическое ожидание и дисперсию случайной величины при заданных параметрах распределения.
Величина равномерно распределена на отрезке [a,b]. Постройте в одной прямоугольной системе координат графики плотности распределения при следующих значениях параметров а и b: а=N-5, b=N; a=N, b=N+5; a=N-5, b=N+5. Постройте в другой прямоугольной системе координат графики функции равномерного распределения при тех же значениях параметра. Объясните качественно поведение графиков. Найдите математическое ожидание и дисперсию случайной величины при заданных параметрах распределения.
Величина распределена по экспоненциальному закону. Постройте в одной прямоугольной системе координат графики плотности распределения при следующих значениях параметра λ: λ= N/10; N/5; N/2. Постройте в другой прямоугольной системе координат графики функции экспоненциального распределения при тех же значениях параметра.
Объясните качественно поведение плотности распределения и функции распределения. Найдите математическое ожидание и дисперсию случайной величины при заданных параметрах распределения.
Величина распределена по нормальному закону. Постройте в двух различных прямоугольных системах координат графики плотности распределения при следующих значениях параметров m и σ:
1) среднее квадратическое отклонение 
постоянно, математическое ожидание m изменяется:
σ =1; m=N-1; N, N+1;
2) среднее квадратическое отклонение 
изменяется, математическое ожидание m постоянно:
m=N; 
, 
, 
.
Постройте в двух других прямоугольных системах координат графики функции нормального распределения при тех же значениях параметров. Объясните качественно поведение плотности распределения и функции распределения. Найдите математическое ожидание и дисперсию случайной величины при заданных параметрах распределения.
Пример выполнения задания 2.1. Вариант 26.
Замечание: в примере выполнения варианта 26 не проведен качественный анализ поведения графиков плотности распределения и функции распределения в зависимости от значений параметров. Предполагается, что студент должен сделать это самостоятельно.
Биномиальное распределение
Распределение Пуассона
Равномерное распределение
Экспоненциальное распределение
Нормальное распределение
1. Среднее квадратическое отклонение постоянно, изменяется математическое ожидание:
2. Математическое ожидание постоянно, изменяется среднее квадратическое отклонение:
Задание 2.2
Вариант 1. Колоду из 52 карт тщательно перемешивают и потом из нее вытаскивают 3 карты. Смотрят эти карты и затем возвращают назад. Такие действия повторяют 10 раз. Найдите вероятность того, что 3 раза будут вытянуты тройка, семерка, туз.
Вариант 2. Радиостанция ведет автоматическую передачу цифрового текста в течении 12 мкс. Работа ее происходит при наличии хаотической импульсной помехи, среднее число импульсов которой в секунду составляет 10000. Для срыва передачи достаточно попадания k импульсов помехи в период работы станции (k=1, 2, 3). Вычислите вероятность срыва передачи станции в течение сеанса работы.
Вариант 3. На зачете преподаватель предлагает студенту наугад выбрать три вопроса из 60. Студент получит зачет, если правильно ответит на все вопросы. На зачет явилось 26 студентов, каждый из которых выучил ответы на 45 вопросов. Какова вероятность того, что не менее половины группы получат зачет?
Вариант 4. Магазин продает в течение одного дня 400 коробок конфет, часть которых с сюрпризом. Вероятность того, что выбранная коробка окажется коробкой с сюрпризом, равна 0,005. Найдите вероятность того, что в течение дня будет продано не менее 5 коробок с сюрпризом.
Вариант 5. Автомобили заезжают на платную автостоянку. Для заезда и оплаты используется автоматический шлагбаум. Время, затрачиваемое на обслуживание одного автомобиля, включая открытие и закрытие шлагбаума, равно 3 минутам. Какова вероятность того, что за это время не подъедет следующий автомобиль, если в среднем поток заезжающих автомобилей составляет 10 автомобилей в час?
Вариант 6. Пара игральных костей бросается 10 раз. Найдите вероятность того, что 5 раз сумма выпавших на игральных костях очков окажется равной шести.
Вариант 7. Провайдер обслуживает 2000 абонентов сети Интернет. Вероятность того, что любой абонент захочет войти в сеть в течение часа, равна 0,002. Найдите вероятность того, что в течение часа более 7 абонентов попытаются войти в сеть.
Вариант 8. С вероятностью 0,65 орудие при выстреле поражает цель. Произведено 400 выстрелов. Найдите вероятность того, что при этом произошло не менее 200 и не более 250 попаданий.
Вариант 9. Оператор принимает заказы на билеты по телефону. В среднем он принимается 10 заказов в час. Оператор был вынужден по указанию начальника прервать прием заказов на 5 минут. Считая все заказы независимыми и пренебрегая временем обслуживания заказа, найдите вероятность того, что в течение этих 5 минут не поступит ни одного звонка.
Вариант 10. В баскетбольной команде процент реализации штрафных бросков равен 60. Найдите вероятность того, что из 100 бросков от 70 до 80 бросков будут успешными.
Вариант 11. Из-за бракованной упаковки в ящике оказались перемешаны сопротивления, имеющие различный номинал, а именно: 100 сопротивлений по 200 Ком, 200 сопротивлений по 100 Ком и 50 сопротивлений по 500 Ком. Из ящика, делая 10 попыток, пытаются достать три сопротивления номиналом 200 Ком за одну попытку. Какова вероятность успешно выполнить задачу 7 раз?
Вариант 12. Вероятность того, что саженец ели прижился и будет успешно расти, равна 0,8. Посажено 400 саженцев ели. Какова вероятность того, что нормально вырастут не менее 250 саженцев ели?
Вариант 13. На факультете обучаются 500 студентов. Найдите вероятность того, что k студентов (k = 0, 1, 2, 3) имеют день рождения 1 апреля. Вероятность определенной даты рождения не зависит от самой даты и даты не зависят друг от друга.
Вариант 14. Прядильщица обслуживает 800 веретен. Вероятность обрыва нитки на одном веретене в течение часа 0,005. Какова вероятность того, что в течение часа нитка оборвется не больше чем на 10 веретенах?
Вариант 15. Вероятность того, что некий прибор безотказно проработает 1 час, равна 0,9. Какова вероятность того, что прибор безотказно проработает сутки?
Вариант 16. Читателю предложено расставить в порядке возрастания или убывания на книжной полке десятитомное собрание сочинений с закрытыми глазами. Перед каждой новой попыткой тома перемешиваются. Какова вероятность того, что в десяти попытках читателю удастся успешно выполнить поставленную задачу три раза?
Вариант 17. Телефонная станция обслуживает 1000 абонентов. В течение часа любой абонент независимо от остальных может сделать вызов с вероятностью 0,005. Найдите вероятность того, что в течение часа было не более 7 вызовов.
Вариант 18. В супермаркете примерно 1% единиц товара оказывается без маркировки. Каждая единица немаркированного товара задерживает покупателя при оплате на 3 минуты. Покупатель выбрал 30 единиц товара. Найдите вероятность того, что он будет задержан при оплате не более чем на 3 минуты.
Вариант 19. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми? Считать, что вероятность дождя в любой день сентября одинакова.
Вариант 20. В каждом из 1000 ящиков 5000 белых и столько же черных пуговиц. Из каждого ящика наугад вынимаются по 3 пуговицы. Какова вероятность того, что число ящиков, из которых вынуты 3 пуговицы одного цвета, не меньше, чем 220 и не больше, чем 260?
Вариант 21. Телефонная книга раскрывается наудачу и выбирается случайно номер телефона. Номер телефона семизначный. Делается пятнадцать попыток. Попытка считается удачной, если все цифры номера окажутся разными. Какова вероятность того, что будет сделано три удачных попытки? Считать, что расположение каждого номера не зависит от расположения остальных и в книге присутствуют все возможные семизначные номера.
Вариант 22. В пакете содержится 50 семян огурцов. Всхожесть семян равна 0,75. При посадке использован весь пакет. Найдите вероятность того, что взойдет 38 семян.
Вариант 23. Корректура в 500 страниц содержит 1300 опечаток. Найдите вероятность того, что на выбранной странице не более трех опечаток.
Вариант 24. По данным телевизионного ателье, в течение гарантийного срока выходит из строя в среднем 12% кинескопов. Какова вероятность того, что из 240 наугад выбранных кинескопов 200 проработают гарантийный срок?
Вариант 25. В Сберегательном банке у кассы для оплаты коммунальных услуг образовалась очередь. Крайний в очереди хочет отойти после того, как за ним займет очередь следующий плательщик. Он прождал 5 минут. Какова вероятность того, что он простоит еще 5 минут, если в среднем занимают очередь 10 человек в час?
Вариант 26. Игральную кость бросают 800 раз. Какова вероятность того, что число очков, кратное трем, выпадает не менее 280 и не более 294 раз?
Пример выполнения задания 2.2. Вариант 26.
Рассмотрим один бросок кости и вычислим вероятность того, что выпадет число очков, кратное трем. Общее количество равновероятных исходов броска - 6 (число очков равно 1, 2, 3, 4, 5,6). Из них количество благоприятных исходов равно 2 (3 и 6). По формуле классического определения вероятности р= 
. Количество бросков n=800 (n>>1), количество выпавших очков, кратных трем, 
(m>>1). Предполагая, что условия предельной интегральной теоремы Муавра – Лапласа выполнены, проведем вычисления в системе Mathcad для получения ответа:
