Тема: Числа, корені, степенева функція
Головні питання:
1. Числа бувають натуральні, цілі, раціональні, дійсні і комплексні. Їх множини позначають відповідно буквами: N, Z, Q, R, C. Кожна з цих множин є частиною (підмножиною) наступної: N ⊂ Z ⊂ Q ⊂ R ⊂ C.
У множині раціональних чисел Q завжди виконуються дії додавання, віднімання, множення і ділення (за винятком ділення на нуль).
2. Обчислення, за умови, що деякі значення виражені у відсотках, називають відсотковими розрахунками. Відсоток (процент) – це сота частина.
1 % = 0,01; 10 % = 0,1; 100 % = 1.
Задачі на відсотки
| Знаходження | Формула | |
| p відсотків від числа a | a ⋅ 0,01 p | |
| Числа, p відсотків якого дорівнюють b дорівнюють b | b: (0,01 p) | |
| Відсоткового відношення | (a: b) ⋅ 100 % | |
| Простих відсотків | Рn = Р0 (1+ 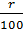 n) n)
| |
| Складних відсотків | Аn = А0 (1+ 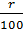 )n )n
|
3. y = f (x) – функція, D – її область визначення, E – область значень. Якщо D і E – множини числові, то y = f (x) – функція числова.
Якщо область визначення числової функції – множина, симетрична відносно 0 і:
1. f (– x) = f (x), то функція y = f (x) парна;
2. f (– x) = – f (x), то функція y = f (x) непарна.
4. Коренем n - го степеня із числа a називають число, n -й степінь якого дорівнює a. Невід’ємний корінь n -го степеня із числа a називають арифметичним значенням кореня n - го степеня із числа a. Його позначають символом 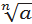 .
.
Приклад. 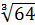 = 4, оскільки 43 = 64,
= 4, оскільки 43 = 64,
 , оскільки 0,15 = 0,00001.
, оскільки 0,15 = 0,00001.
5. Обчислення значення коренів n -го степеня із чисел називають добуванням коренів із цих чисел.
6. Властивості коренів n -го степеня:
 =
=  *
* 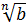 ; 2)
; 2) 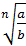 =
= 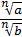 ; 3)
; 3) 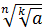 =
= 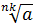 ;
;
 =
=  ; 5)
; 5) 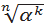 = (
= (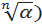 k
k
7. Степені з дробовими показниками: 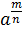 =
= 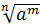
Властивості. Якщо r і s – числа раціональні, то:
 *
* 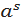 =
= 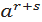 2)
2)  :
: 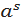 =
= 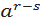 3) (
3) ( s =
s = 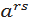
4) (ab)r = 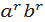 ; 5)
; 5)
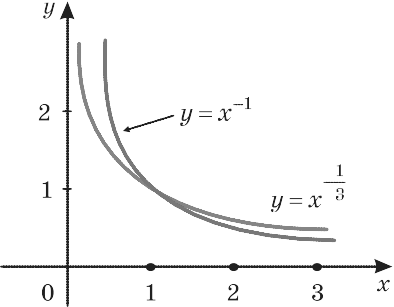
8. Степенева функція  ;
;  ;
; 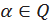 .
.
Властивості: функція монотонна, ні парна, ні непарна.
При α > 0 функція зростаюча, при α < 0 – спадна.
Графік функції проходить через точку М (1; 1).
y = x α, α > 0 y = x α, α < 0

9. Рівняння називають ірраціональним, якщо воно містить змінну під знаком кореня або в основі степеня з дробовим показником. Найзагальніший спосіб розв’язування ірраціональних рівнянь – піднесення обох його частин до однакових степенів з наступним відкиданням сторонніх розв’язків. Багато ірраціональних рівнянь зручно розв’язувати за допомогою заміни змінної.
Тема: Тригонометричні функції
Головні питання:
1. 1 рад = 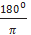 ≈ 57°18′.
≈ 57°18′.
2.Основні тригонометричні формули:
sin2 α + cos2 α= 1,
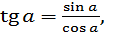
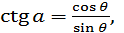 tg α ⋅ ctg α = 1. r
tg α ⋅ ctg α = 1. r
3.Формули зведення:
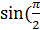 -
- 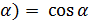 ,
,  -
- 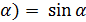 , tg = (
, tg = ( = ctg
= ctg  .
.
sin (π + α) = –sin α, cos (π + α) = –cos α, tg (π + α) = tg α.
4.Правило зведення: якщо кут даної тригонометричної функції відкладається від вертикального діаметра, то її замінюють кофункцією, якщо ж – від горизонтального діаметра, то її назву не змінюють. Знак ставлять такий, який має значення даної функції за умови, що кут α гострий.
Формули додавання і наслідки з них
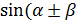 ) = ) = 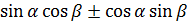
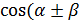 )= )= 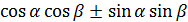
| 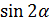 = = 
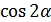 = = 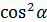 - - 
|
  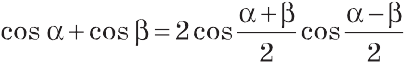     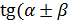 )= )= 
| 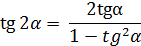
|
Формули перетворення тригонометричних функцій
7. Тригонометричні функції та їхні графіки
y = sin x, D = R, E = [–1; 1], графік – синусоїда;
y = cos x, D = R, E = [–1; 1], синусоїда, зміщена на 
y = tg x,, х 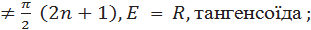
y = ctg x, х  , E = R
, E = R
y = A sin (ω t +  ) – гармонічне коливання.
) – гармонічне коливання.
А – амплітуда;
ω – кутова швидкість;
ω t +  – фаза коливання;
– фаза коливання;
 – початкова фаза.
– початкова фаза.






