Пусть 
− произвольный базис n – мерного евклидова пространства (существование такого базиса обусловлено n – мерностью пространства). Алгоритм построения по данному базису ортонормированного заключается в следующем:
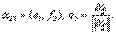
Аналогично 
Продолжая процесс, получаем ортонормированный базис 
, где
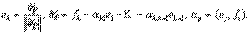
13. Определение 4.3. Ненулевой вектор x в линейном пространстве L называют собственным вектором линейного оператора A: L → L, если для некоторого действительного числа λ выполняется соотношение Ax = λx. При этом число λ называют собственным значением (собственным числом) линейного оператора A. Определение. Множество всех собственных значений линейного оператора называют спектром линейного оператора. Определение 4.2. Характеристическим многочленом линейного оператора A: L → L называют характеристический многочлен его матрицы A, записанной в некотором базисе, а характеристическим уравнением этого оператора — характеристическое уравнение матрицы A.
14. Теорема 4.5. Пусть собственные значения λ1,..., λr линейного оператора A попарно различны. Тогда система соответствующих им собственных векторов e1,..., er линейно независима. Теорема 4.6. Матрица линейного оператора A, действующего в линейном пространстве, в данном базисе является диагональной тогда и только тогда, когда все векторы этого базиса являются собственными для оператора A. Следствие 4.1. Если характеристическое уравнение линейного оператора, действующего в n-мерном линейном пространстве, имеет n попарно различных действительных корней, то существует базис, в котором матрица этого оператора является диагональной. Следствие 4.2. Если характеристическое уравнение квадратной матрицы порядка n имеет n попарно различных действительных корней, то эта матрица подобна некоторой диагональной.
15. Определение 5.2. Линейный оператор A, действующий в евклидовом пространстве, называют самосопряженным, если A∗ = A. Это определение можно сформулировать по-другому. Линейный оператор самосопряженный, если для любых векторов x и y верно равенство (Ax, y) = (x, Ay). Теорема 5.2. Матрица самосопряженного оператора в любом ортонормированном базисе является симметрической. Наоборот, если матрица линейного оператора в некотором ортонормированном базисе является симметрической, то этот оператор — самосопряженный. Теорема 5.3. Все корни характеристического уравнения самосопряженного оператора действительны. Следствие 5.1. Если матрица A является симметрической, то все корни ее характеристического уравнения det(A − λE) = 0 действительные. Следствие 5.2. Самосопряженный оператор, действующий в n-мерном евклидовом пространстве, имеет n собственных значений, если каждое из них считать столько раз, какова его кратность. Следствие 5.3. Симметрическая матрица порядка n имеет n собственных значений, если каждое из них считать столько раз, какова его кратность.
А.
Определение 5.1. Линейный оператор A∗: E → E называют сопряженным к линейному оператору A: E → E, если для любых векторов x, y ∈ E верно равенство (Ax, y) = (x, A∗y). Лемма. Если квадратные матрицы M и N порядка n таковы, что для любых векторстолбцов x, y ∈ Rn выполняется соотношение xтMy = xтNy, то M = N. Теорема 5.1. Любому линейному оператору A: E → E соответствует единственный сопряженный оператор A∗, причем его матрицей в любом ортонормированном базисе e является матрица Aт, транспонированная матрице A линейного оператора A в том же базисе e.
16. 
17. 
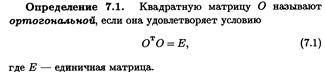
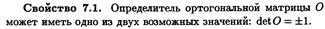
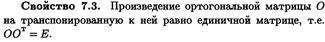
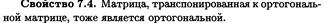
18. 
19. 
23. 
10. 
11. 
12. 
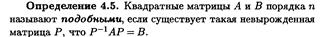
20. 
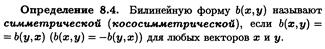
21. 
22. 
24. 
25.
