Лекция 2
Аминокислоты, из которых сложена полипептидная цепь (Рис.2-1), могут находиться в двух стерических формах: L и D.
Рис.2-1. Боковые цепи двадцати стандартных аминокислотных остатков, исходящие из Сa атомов главной цепи. Белыми кружками показаны Сa атомы главной цепи, серыми — С атомы боковых групп, светло-серыми — H атомы боковых групп, синими — N атомы боковых групп, красными — O атомы боковых групп, желтыми — S атомы боковых групп.
Эти формы, L и D, зеркально-симметричны: в них массивный боковой радикал (R) и Н-атом, стоящие при a-углероде (Сa) аминокислоты, меняются местами (стрелки указывают углубление атомов в рисунок):
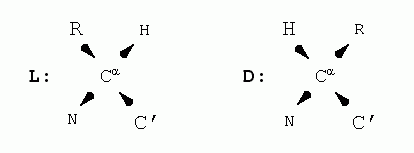
L и D форм нет только у глицина (Gly), "боковая цепь" которого состоит лишь из Н-атома.
Белковые цепи сложены только из остатков L-аминокислот. Только они кодируются генами. D-аминокислотные остатки — они встречаются в пептидах — не кодируются при матричном синтезе белка, а синтезируются специальными ферментами. Рацемизация (L «D переход) спонтанно в белках практически не происходит. Не происходит она и при биосинтезе, — хотя часто встречается при чисто химическом синтезе пептидов, где на борьбу с рацемизацией уходит много сил.
Аминокислоты в белковой цепи связаны между собой пептидными связями C' и N атомов (Рис.2-2).
Рис.2-2. Полипептид: главная цепь и боковая группа (Ser) на ней. Пептидные группы заштрихованы. Показаны углы внутреннего вращения в главной (f, y, w) и боковой (c) цепях. Стрелки указывают направление вращения, ведущее к росту угла поворота ближней к нам части цепи относительно более отдаленной ее части. Картинка взята из [3] и адаптирована.
Важную роль в структуре белка играет как жесткость этих связей, так и плоская форма всей пептидной группировки
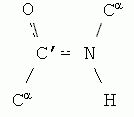
И то, и другое обеспечивается так называемой sp2-гибридизацией электронов N и С' атомов. "Гибридизация" электронных орбит — это чисто квантовый эффект. Sp2-гибридизация преобразует одну сферическую s- и две вытянутые p-орбиты электронов атома в три sp2-орбиты. Эти три орбиты вовлекают атом в три ковалентные связи, лежащие в одной плоскости (-·<). Вовлеченные в sp2-гибридизацию электроны ковалентно связанных C' и N атомов создают "делокализованное" электронное облако, охватывающее оба эти атома, и распространяющиеся также — через связь С-О — на атом О (именно поэтому связи C' 
N и C O рисуются как равноправные "полуторные", ). Но у C и N атомов есть еще p-электроны кроме тех, что уже задействованных в sp2 орбитах! И так как эти p-орбиты имеют форму "восьмерок", перпендикулярных всем трем sp2-орбитам (-·<), то дополнительная связь этих p-электронов — связь, требующая сближения "восьмерочных" орбит и "обобществления" (т.е. переходов с атома на атом) находящихся на них электронов,
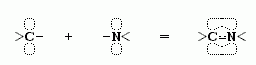
— это обобществление p-электронов препятствует вращению вокруг С'-N связи.
Хочу напомнить, что делокализация электронов, их переход с атома на атом — основная причина образования химических связей. Это следует из принципа неопределенности Гайзенберга:
DpDx» 
| (2.1) |
Здесь Dp — неопределенность в импульсе частицы, Dx — неопределенность в ее координате, а º h/2p, где h — постоянная Планка. Так как направление движения электрона в атоме не может быть известно, то Dp» |p| = mv, где v — скорость, а m — масса частицы. Следовательно,
v» /(mDx).
В то же время, кинетическая энергия частицы E = mv2/2, т.е.
| E» 2/(mDx2).
| (2.2) |
Следовательно, при делокализации, когда Dx возрастает, — энергия частицы падает, и она переходит в более стабильное состояние. Видно, что этот эффект наиболее силен для легких частиц — т.е. электронов. Так делокализация электрона приводит к химической связи.
Длина химической связи близка к Вандерваальсову радиусу атома, т.е. составляет 1 — 2 
(точнее: около 1 — для связи C-H, N-H или O-H, около 1.2 — 1.3 — для С=О, C O, C N и С=С, 1.5 — для С-С, и около 1.8 — для S-S).
Характерные величины валентных углов составляют около 120о и около 109о. Углы в 120о находятся при sp2-гибридизованных атомах типа -C'<, -N<, где три валентные связи направлены из центра к вершинам плоского треугольника, углы в 109о — при sp3-гибридизованных атомах типа >Ca<, где четыре связи направлены из центра к вершинам тетраэдра, а также при завязывающих по две связи O< или S< атомах.
Остановимся теперь на характерных величинах флуктуаций, т.е. тепловых колебаний валентных связей и углов. Они могут вносить вклад в гибкость белковой цепи.
Частоты колебаний проявляются в инфракрасных (ИК) спектрах белков. Характерные частоты колебаний таковы: n ~ 7x1013 сек-1 — для колебания атома Н, — например, в С-Н связи (при этом длина волны l=c/n~5мк); и n ~ 2x1013 сек-1 — для колебания "тяжелых" групп, — например, в СН3-СН3 связи (при этом l=c/n~15мк; здесь c — скорость света, 300000 км/сек).
Возбуждены ли эти колебания теплом при комнатной температуре?
Для ответа на этот вопрос мы должны сравнить тепловую энергию, приходящуюся на одну степень свободы ("тепловой квант" kT) с энергией колебания. Оценим величину kT при "нормальной" температуре. Здесь T — абсолютная температура в градусах Кельвина (Т=300оК при 27оС, т.е. при примерно "комнатной" температуре; К — обозначение градуса Кельвина), а k (иногда еще пишут kB) — постоянная Больцмана [равная 2 (кал/моль)/К, или 0.33x10-23 кал/К в расчете на одну частицу, так как в одном моле — 6x1023 частиц]. Значит, при комнатной температуре "тепловой квант" kT = 600 кал/моль, или (600кал)/(6x1023 частиц), т.е. 10-21 калорий на частицу.
Соответствующую такому тепловому кванту частоту nT можно найти из соотношения kT = hnT [где постоянная Планка hº2p =6.6x10-34 Джxсек = 1.6x10-34 калxсек; напомню, что 1 калория (кал) = 4.2 джоуля (Дж)]. Итак, частота nT равна 7x1012 сек-1 при T=300K, т.е. при 27оС.
"Тепловой квант" не может возбудить более жесткие, более частые, чем он сам, колебания.
Значит, при комнатной температуре валентные связи "тверды" и не флуктуируют: для этих связей частота колебаний n ~ 2x1013 — 7x1013 сек-1, т.е. она на порядок больше, чем nT = 7x1012 Джxсек-1.
Однако валентные связи могут раскачиваться падающим инфракрасным светом, и на этом основана ИК-спектроскопия белков. Собственно, именно ИК спектроскопия и дает сведения о колебаниях атомов, валентных связей и валентных углов. Конечно, экспериментально их исследуют на малых молекулах, а затем полученную информацию используют при изучении белков.
В отличие от колебаний длин связей, тепловые колебания валентных углов, на порядок более мягкие, — их частоты лежат в пределах 1012 — 1013 сек-1, — возбуждены при комнатной температуре. Однако их характерная амплитуда невелика — около 5о.
Итак, колебания валентных связей вовсе не вносят вклада в гибкость белковой цепи, а колебания валентных углов вносят весьма скромный вклад. На самом деле гибкость белковой цепи, а значит — и ее способность складываться и в a спирали, и в глобулы обеспечивается вращением (хотя и не вполне свободным вращением, см. ниже) вокруг валентных связей. Поэтому и структура цепи в целом часто описывается просто в терминах углов вращения вокруг валентных связей — тогда она называется "конформацией". Впрочем, очень часто термины "структура" и "конформация" употребляются просто как синонимы.
Основные сведения о вращении атомных группировок вокруг валентных связей тоже поставляет ИК-спектроскопия; как и раньше, я остановлюсь только на результатах.
Взаимное расположение атомных группировок, связанных валентной связью, описывается двугранным углом (двугранным — так как это угол между двумя плоскостями — "гранями"). Рисунки 2-2, 2-3 иллюстрируют отсчет этого угла. Отсчет — такой же, как в школьной тригонометрии, если рассматривать ближнюю к нам валентную связь как "вращающуюся стрелку", дальнюю от нас — как "координатную ось", а центральную валентную связь — как "ось вращения". То есть вращение "стрелки" против хода часов увеличивает угол поворота, а по ходу — уменьшает.
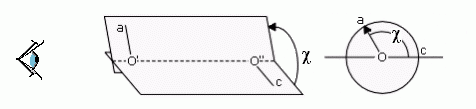
Рис.2-3. Отсчет величины двугранного угла (угла поворота): вид поперек (слева) и вдоль (справа) оси вращения. Дальняя от нас валентная связь 0''— c — "ось координатного круга", центральная связь 0'— 0'' — "ось вращения", ближняя к нам связь 0'— a — "стрелка на координатном круге".
Рисунок 2-4 показывает характерное поведение энергии при вращении вокруг связи, соединяющей два sp3-гибридизованных атома (на примере Н3С-СН3 и СН2С-СН2С связей). Такие связи характерны для алифатических боковых групп. Углы вращения боковых групп называются углами w, "хи" (см. Рис.2-2). Максимумы такого трехкратного (соответственно симметрии sp3-sp3 связи) потенциала (т.е. потенциала, имеющего три максимума и три минимума при повороте на 360o) соответствуют трем "затененным" конформациям (0о, +120о и -120о), приводящим к сближению (и отталкиванию) электронных облаков. Эти облака отталкиваются, так как образующие их электроны уже задействованы в ковалентных связях. Величина возникающих при этом потенциальных барьеров вращения вокруг Н3С-СН3 связи — около 3 ккал/моль, а характерный размах тепловых флуктуаций вокруг этих минимумов (т.е. те отклонения от них, при которых энергия возрастает на kT) — 15-20о.
Рис.2-4. Характерный потенциал вращения вокруг одинарной связи между двумя sp3-гибридизованными атомами: вокруг Н3С-СН3 связи (красная кривая) и вокруг (С-СН2)-(СН2-С) связи (синяя кривая). Главный энергетический эффект дает отталкивание электронных облаков: оно максимально в "затененной" конформации (при 0, 120, 240о) и минимально в "скрещенной" (при 60, 180, 300о). Отталкивание маленьких Н-атомов несущественно. Однако отталкивание тяжелых, окруженных большими электронными облаками С-атомов в окрестности 0о создает добавочный энергетический эффект, отличающий поворот вокруг (С-СН2)-(СН2-С)связи от поворота вокруг (Н3С)-(СН3) связи. Для сравнения, стрелкой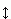 
отмечена величина kT.
Когда некоторые из валентностей при sp3 гибридизованных атомах заняты не водородами, а более массивными атомами — их отталкивание повышает соответствующую слишком тесному сближению этих массивных атомов часть барьера. Это показано на Рис.2-4 на примере вращения вокруг центральной связи в (С-СН2)-(СН2-С).
Рисунок 2-5 показывает характерное поведение энергии при вращении вокруг пептидной связи, соединяющей два sp2-гибридизованных атома (С' и N). Угол вращения вокруг этой связи называется углом w (Рис.2-2). Потенциал двукратен (т.е. имеет два максимума и два минимума при повороте на 360o), соответственно симметрии sp2-sp2 связи. Потенциальные барьеры велики из-за участия в пептидной связи p-электронов (как о том говорилось в начале лекции), минимумы потенциала приходятся на 0o и 180o (где p-орбиты, стягивающие С'- и N-атомы, наиболее сближены), а его максимумы — на 90o и 270o (где эти стягивающие p-орбиты наименее сближены и, следовательно, хуже всего связаны друг с другом). Из-за высоких барьеров характерный размах тепловых флуктуаций угла вращения вокруг таких связей невелик — около 10о.
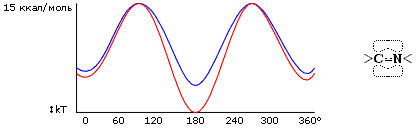
Рис.2-5. Характерный потенциал вращения вокруг кратной связи, соединяющей два sp2-гибридизованных атома (С' и N) в пептидной связи. Справа показана связь электронных p-орбит при угле, равном 0o (или 180o). Для всех (за исключением пред-пролиновых) пептидных связей энергия (красная кривая) при 0о выше, чем при 180о, из-за отталкивания массивных Ca-атомов. Эта разность энергий мала для пептидной связи, находящейся перед Pro (синяя кривая), имеющим не один, а два С-атома при N-атоме. См. текст и рисунок, где приведена структурая формула пролина.
Стоит отметить, что отталкивание массивных Ca атомов делает cis конформацию (w=0о) энергетически довольно невыгодной; поэтому почти все пептидные группы в белках находятся в trans конформации (w=180о).
Исключение составляет пептидная связь, предшествующая пролину (имино -, а не амино кислоте): в Pro — два почти симметричных массивных радикала при N атоме (-СaНС2 и -СН2С, см. Рис.2-1), так что для этой связи trans конформация лишь ненамного лучше, чем cis.
И в глобулярных белках, и в развернутых (т.е. флуктуирующих, не имеющих фиксированной структуры) пептидах наблюдается около 90% trans и 10% cis пролинов. Хочу обратить ваше внимание на эту закономерность — что выгодно само по себе, то чаще встречается и в глобулярных белках. Мы столкнемся с ней еще не раз.
Наконец, рассмотрим потенциал вращения вокруг связи, соединяющей sp3 гибридизованный и sp2 гибридизованный атомы. Углы вращения вокруг такой связи называются углами f (вращение вокруг N-Ca связи) и y (вращение вокруг Ca-С' связи) (Рис.2-2). При вращении по каждому из них возникает шестикратный (6 минимумов и 6 максимумов при повороте на 360o) потенциал с довольно низкими барьерами (Рис.2-6): их высота,»1 ккал/моль — порядка энергии тепловых колебаний (составляющей, как мы помним, 0.6 ккал/моль при комнатной температуре). Именно почти свободное вращение по углам f и y вокруг такого рода связей (между N и Сa и между Ca и C') в главной цепи полипептида и обеспечивает основную гибкость белковой цепи.
Рис.2-6. Характерный потенциал вращения вокруг одинарной связи между sp3- и sp2-гибридизованными атомами (на примере вращения вокруг Н3С-С5Н6 связи).
Лекция 3
Рассмотрим теперь элементарные взаимодействия атомов, не связанных ковалентно друг с другом.
Но сначала вспомним, что основная причина образования химических связей — делокализация электронов, их "переход" с атома на атом и обратно — или, как говорят, пребывание электронов на совместной, "обобществленной" орбите, охватывающей два атома. При этом, согласно запрету Паули, в одном месте, на одной орбите может находиться не более двух электронов, — причем тогда их "спины" (т.е. моменты вращения электронов) должны быть противоположно направлены (или, как говорят, "спарены"). Спаривание двух электронов на одной совместной орбите (когда один электрон пришел от одного атома, а второй — от другого) ведет к прочной ковалентной связи.
Если же у сближающихся атомов и так на каждой орбите — по два спаренных электрона, то эти атомы не могут образовать ковалентную связь. Иначе на каждой обобществленной орбите электронов было бы слишком много — четыре. А, согласно запрету Паули, одна орбита может вынести не более двух! Значит, уже насыщенные, заполненные электронной парой орбиты не могут далее обобществляться. И потому несущие такие "насыщенные" орбиты атомы отталкиваются на малых расстояниях, когда их электронные облака начинают перекрываться. Такие атомы непроницаемы друг для друга при обычных (не космических) температурах.
То же происходит, если в сближающихся молекулах все их валентности уже насыщены: они отталкиваются, когда их атомы сближаются до 2-3 .
Однако на больших расстояниях (когда нет перекрывания электронных облаков) все атомы и молекулы притягиваются — если только у них нет электрического заряда, о чем мы поговорим позже. Притяжение это имеет чисто квантовую основу. Оно связано с коррелированными, т.е. согласованными колебаниями электронов в обоих атомах. Дело в том, что энергия пары атомов, где электроны смещены (поляризованы) одинаковым образом, — чуть меньше, чем энергия пары неполяризованных атомов. Это ясно из следующей схемы (здесь два атома, "1" и "2", и у каждого — электрон "-" и ядро "+")
Глядя на схему, нужно помнить, что электрическая энергия растет с уменьшением расстояния r как 1/r. В результате смещения электронов взаимодействия электрон-электрон и ядро-ядро не меняются, но (рассмотрим самый правый рисунок) усиливается притяжение электрона 1 к ядру 2 — причем оно усиливается больше, чем ослабевает притяжение электрона 2 к ядру 1. Поэтому согласованное колебание электронов (а это и есть квантовый эффект) понижает энергию системы. При отдалении атомов их взаимодействие ослабляется. В результате энергия взаимодействия спадает с расстоянием r между ядрами атомов — можно показать, что она спадает пропорционально (1/r)6.
Общая энергия взаимодействия атомов — она еще называется энергией Вандерваальсова взаимодействия — охватывается рисунком 3-1 и приближенно описывается формой Леннард-Джонса:
| ULD(r) = E0[(r0/r)12 - (r0/r)6] | (3.1) |
Здесь r0 — как легко проверить, взяв производную ULD по расстоянию r — есть то расстояние, на котором энергия ULD проходит через минимум, а -E0 — глубина этого минимума. Последний член формулы (3.1) — тот, что падает с расстоянием, как (const /расстояние)_в_шестой_степени — соответствует притяжению (знак "минус" перед ним указывет, что соответствующая энергия падает при сближении); а тот, где значится двенадцатая степень, соответствует отталкиванию (этот член положителен, т.е. соответствующая ему энергия растет при сближении).
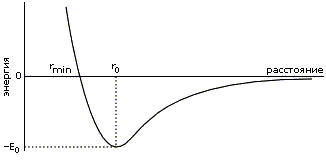
Рис.3-1. Характерный вид потенциала Вандерваальсова взаимодействия.
Формула 3.1 точно описывает только притяжение на больших (когда r << r0) расстояниях. Отталкивание на малых расстояниях она описывает только качественно, как "очень сильное отталкивание, превосходящее любое притяжение, когда r стремится к нулю". То, что формула (3.1) — приближенная, видно хотя бы по тому, что она подразумевает округлость атомов (т.к. ею описываемое взаимодействие не зависит от направления), — а электронное облако у атома, вообще говоря, не круглое, — вспомните хотя бы о торчащих p-электронах. Вообще, правильно и совсем корректно взаимодействие атомов описывает только квантовая механика — но точно рассчитать она может только очень простые системы, вроде атома Не, иона Н2+ или молекулы Н2. Для всего остального приходится брать приближенные, "полуэмпирические" формулы — вроде (3.1) — где вид формулы берется из качественных физических соображений, а параметры (у нас — E0 и r0) — подбираются из опыта. Некоторые основные данные сведены в Таблицу 3/1.
Таблица 3/1. Характерные параметры потенциалов Вандерваальсовых взаимодействий
| Взаимодействие | E0, ккал/моль | r0,
| rmin,
| Вандерваальсов радиус атома,
| |
| H.... H | 0.12 | 2.4 | 2.0 | H: | 1.0 |
| H.... C | 0.11 | 2.9 | 2.4 | ||
| C.... C | 0.12 | 3.4 | 3.0 | C: | 1.5 |
| O.... O | 0.23 | 3.0 | 2.7 | O: | 1.35 |
| N.... N | 0.20 | 3.1 | 2.7 | N: | 1.35 |
| CH2... CH2 | »0.5 | »4.0 | »3.0 | CH2: | »1.5 |
Примечания. Величины E0, r0 для межатомных взаимодействий взяты из R.A.Scott, H.A.Scheraga, J. Chem. Phys. (1965) 45:2091, а величины rmin — из G.N.Ramachandran, V.Sasisekharan, Adv. Prot. Chem. (1968) 23:283. Исходя из этих величин, оценены параметры взаимодействия CH2...CH2. Взаимодействие CH2...CH2 зависит от взаимной ориентации этих групп; поэтому приведенные в таблице числа — приблизительные; их, однако, часто приходится использовать, так как рентген "не видит" водородных атомов в белках.
Обратите также внимание на то, что в таблице дано не только оптимальное расстояние r0, но и rmin — минимальное расстояние, на котором соответствующие атомы встречаются в кристаллах. rmin примерно соответствует той точке Рис.3-1, где энергия при сильном сближении проходит через 0.
Расстояния (r0, rmin) и энергии (E0) в основном берутся из кристаллов — из их структур (расстояния) и теплот сублимации (энергии). Но кристаллы обычно состоят не из атомов, а из молекул. Например: СН4, С2Н6,... Так что при расчете энергии всегда возникают вопросы типа: каков вклад С...С, каков — Н...Н, каков — С...Н взаимодействий? Разные авторы решают его по-разному — поэтому потенциалы у них порой заметно расходятся. Надо помнить, что нельзя самодеятельно брать одни параметры (например, энергию С...С взаимодействия) у одного автора, а другие — у другого: тут действует принцип "все или ничего", иначе будут ошибки.
Приведенные в таблице величины помогают понять, почему trans- конформация С' N связи допустима, а ее cis- конформация — нет (для всех аминокислотных остатков, кроме пролина, о чем мы уже говорили): в trans- конформации С' N связи расстояние между Сaатомами равно 3.8 , а в cis- (когда эти атомы наиболее сближены) — всего 2.8 , что меньше минимально допустимого расстояния rMIN, равного 3.0 для пары С...С.
Из-за жесткости trans- формы С' N связи и из-за того, что в ней Ca-атомы соседних по цепи аминокислот довольно далеко отстоят друг от друга, соседние по цепи остатки могут менять свою конформацию почти независимо друг от друга. Но внутри остатка вращения по углам f и y взаимосвязаны. Изображенные в координатах (f, y) "разрешенные" и "запрещенные" конформации остатка называются картами Рамачандрана (или, более корректно, — картами Рамачандрана-Сасисекхарана).
Прежде чем рисовать их, — посмотрим, какие конформации разрешены (и какие — нет) при вращении по углу f (вокруг N-Ca связи) и по углу y (вокруг Ca-С' связи) в отдельности.
Мы уже знаем, что вращение вокруг этих связей (соединяющих sp3-гибридизованный Сa-атом с sp2-гибридизованными N или C') практически свободно. Однако в cis- конформациях (при f=0o или y=0o) вращающиеся вокруг таких связей атомы (C'i-1 и C'i при вращении по углу f вокруг N-Ca связи, и атомы Ni и Ni+1 при вращении по углу y вокруг Ca-C' связи, см. Рис.3-2; i-1, i, i+1 - номера последовательных остатков в цепи) сближаются особенно сильно, и здесь возможен запрет конформации из-за отталкивания этих атомов — как говорят, стерический запрет.
Рис.3-2. Так выглядела бы карта запрещенных 
, напряженных 
и полностью разрешенных 
конформаций при вращении по углам f, y во фрагменте CaC'N - Ca - C'NCa, если бы ко всем этим атомам не было бы прикреплено больше никаких других (см. справа).
Следующая схема показывает, что минимальное расстояние между атомами C'i-1 и C'i (при вращении по f) и между атомами Ni и Ni+1 (при вращении по y) — одно и то же, 2.9 : это чуть меньше, чем rMIN=3.0 для C...C взаимодействия (так что здесь cis конформация запрещена), — и чуть больше, чем rMIN=2.7 (хоть и меньше, чем r0=3.1 ) для N...N взаимодействия (так что здесь cis конформация не запрещена, но напряжена).
Если бы дело ограничивалось только этими С и N атомами, карта запрещенных , напряженных и разрешенных конформаций выглядела бы так, как на Рис.3-2. При этом вращения по углам f и y не были бы взаимосвязаны.
Однако при атоме C' есть О и Ca атомы, а при N — есть H и C' атомы (причем в воде к Н-атому жестко приторочена водородной связью молекула Н2О, см. ниже). Так что в результате карта Рамачандрана — карта запрещенных и разрешенных конформаций самого маленького аминокислотного остатка, глицина (боковой радикал -Н) — выглядит, на как Рис.3-3.
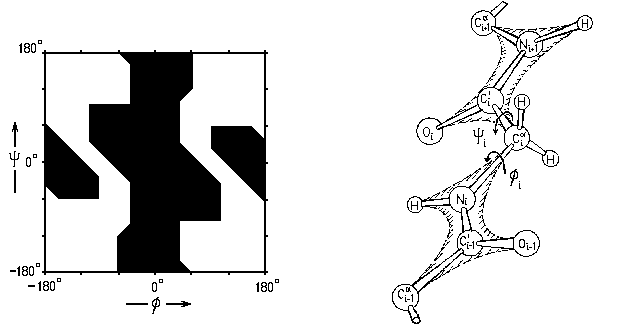
Рис.3-3. Карта запрещенных и разрешенных конформаций глицина (Gly) при вращении по углам f, y в белковой цепи.
У глицина нет массивного бокового радикала. У всех остальных аминокислотных остатков он есть, и столкновение этого радикала (точнее, его ближайшего к главной цепи Сb-атома) с C'-атомом вырубает запрещенную область по углу f, а с N-атомом — запрещенную область по углу y (Рис.3-4).
Рис.3-4. Карта разрешенных конформаций аланина (Ala) при вращении по углам f, y в белковой цепи; — области, разрешенные лишь для глицина; — области, запрещенные для всех остатков взаимодействиями в главной цепи.
Нарисованная на Рис.3-4 карта относится к аланину, боковой радикал которого мал: СbН3-группа. У всех остальных аминокислотных остатков радикал крупнее — с одним или двумя тяжелыми g атомами при Сb-атоме. Однако от главной цепи эти "новые" g (и еще более далекие d, e и т.д. атомы) находятся далеко, и потому мало влияют на карту Рамачандрана. Точнее: в небольшой (оставленной белой на Рис.3-5) области столкновений этих g-атомов с главной цепью нет вообще, а в других разрешенных для аланина конформациях они могут быть — при некоторых конформациях радикала - и потому здесь разрешены не все конформации радикала; эти области я слегка заштриховал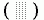 
на Рис.3-5.
Рис.3-5. Карта запрещенных и разрешенных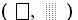 
конформаций более крупных остатков при вращении по углам f, y в белковой цепи. В области разрешены все конформации боковой группы по углу c1, в области 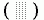часть углов c1 запрещена.
Столкновения g атомов с главной цепью особенно существенны для валина, изолейцина и треонина, имеющих по два крупных g атома.
В заключение рассмотрим карту Рамачандрана для иминокислоты пролина. У него угол f практически фиксирован при —70о кольцом, образуемым боковой группой Pro при участии N-атома его главной цепи, а вращение по углу y — такое же, как у аланина. Так что его разрешенные конформации выглядят, как белая область на карте, Рис.3-6.
Рис.3-6. Карта разрешенных для пролина конформаций на фоне конформаций, разрешенных для аланина ; — конформации, запрещенные для них обоих.
Кольцо пролина сужает и область разрешенных конформаций остатка, лежащего перед ним в цепи (Рис.3-7).
Рис.3-7. Область разрешенных конформаций остатка аланина, лежащего перед пролином в белковой цепи. Область 
была бы разрешена, если бы не пролин.
Наконец — посмотрим, как все эти теоретические выкладки (суммируемые Рис.3-3 для Gly и Рис.3-4 для прочих аминокислот) согласуются с наблюдаемыми (рентгеном) в белках конформациями аминокислотных остатков (на Рис.3-8 они отмечены точками, для Gly и для прочих аминокислотных остатков в отдельности). Как видим, согласие это весьма хорошее.
Рис.3-8. Наблюдаемые в белках конформации аминокислотных остатков (точки) для глицина (справа) и для всех остальных остатков (слева). Контур очерчивает стерически разрешенные области. Картинка взята из [5] и адаптирована.
Мы видим, что подавляющее большинство экспериментальных точек попадает в "стерически разрешенные" области. Однако некоторые точки лежат в "стерически запрещенных" областях. Последнее не удивительно, так как мы назвали "стерически запрещенными" те области, где энергия просто высока — не бесконечно велика, что, конечно, привело бы к полному запрету, — а скажем, на пару ккал/моль больше, чем в конформации с минимальной энергией. То есть белку надо затратить энергию, чтобы загнать аминокислотный остаток в такую область, но он вполне может это сделать. Может сделать, но делает редко.
По ходу лекций мы убедимся, что это — общее правило: напряженные, высокоэнергетичные элеметы в белках встречаются редко — но все же встречаются. Что не удивительно: раз белок стабилен, он должен состоять, — в массе, но не обязательно целиком, — из стабильных деталей.
Лекция 4
До сих пор мы не учитывали водного окружения белков. Пора восполнить этот пробел.
Вода — весьма своеобразный растворитель. Прежде всего — она кипит и затвердевает при аномально высоких, для ее малого молекулярного веса, температурах. Действительно, вода — Н2О — кипит при 373оК, а твердеет при 273оК, в то время как О2 кипит при 90оК и твердеет при 54оК; Н2 кипит при всего 20оК и плавится при 4 оК; СН4 кипит при 114оК, и т.д. То, что структуры воды и льда с трудом разрушаются теплом, показывает, что молекулы воды чем-то очень сильно связаны между собой.
Это "что-то" — связь между О и Н атомами молекул Н2О (именно между О и Н, так как и О2, и Н2 в отдельности легко кипят и плавятся). Эта связь называется водородной связью.
Водородные связи наблюдаются не только в воде. Они наблюдаются всегда, когда водород химически связан с одним электроотрицательным (т.е. притягивающим электрон) атомом и при этом приближается к другому электроотрицательному атому. Примеры: O—H::: O, N—H::: O, N—H::: N. Но С-H группа, например, водородных связей не образует: атом С — недостаточно электроотрицательный атом.
Основные особенности воды как растворителя связаны с наличием в ней мощных водородных связей.
Водородная связь молекул воды носит электрическую природу. То, что она связана именно с электронами и зарядами, а не с ядрами водородных атомов, прямо следует из того, что температуры и теплоты кипения и плавления легкой (Н2О) и тяжелой (D2О) воды практически совпадают, — несмотря на двукратное различие в массах ядер D и Н.
Молекула воды полярна. Это значит, что на ее атомах есть небольшие ("парциальные") электрические заряды: на электроотрицательном О — отрицательный, на Н — положительный. Распределение зарядов и электронных облаков на этих атомах выглядит так:
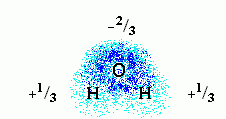
Здесь плотность электронного облака показана плотностью точек, а цифры показывают парциальный заряд атомов этой полярной молекулы. Заряд этот выражен в долях от протонного заряда. У протона, в этих единицах, заряд, естественно, равен +1, а у электрона -1. В целом молекула воды имеет заряд 0.
Заряды на полярных атомах появляются в результате того, что электроотрицательные атомы O оттягивают электронные облака от соседних Н атомов. В результате на последних возникают небольшие положительные заряды, а на O — отрицательный заряд.
Как вы помните, заряды q1 и q2 на расстоянии r взаимодействуют в вакууме с энергией
| U = q1q2/r. | (4.1) |
В вакууме заряды взаимодействуют очень сильно. Энергия взаимодействия двух единичных (т.е. протонных или электронных) зарядов на расстоянии 1 близка к 330 ккал/моль (запомните эту цифру: она нам пригодится для разных дальнейших оценок), а на более реалистичном (учитывая Вандерваальсово отталкивание атомов) расстоянии 3 эта энергия близка к 110 ккал/моль. Энергия взаимодействия единичных зарядов — это характерная энергия химической связи; она в сотни раз больше, чем характерная тепловая энергия kT или характерная энергия Вандерваальсового взаимодействия атомов.
Парциальные заряды молекулы воды меньше и потому взаимодействуют слабее — с энергией порядка 10 ккал/моль на расстоянии 3 , но и такой энергии хватает на то, чтобы, при притяжении Н к О, "промять" электронные оболочки атомов. Особенно этот эффект "проминания" облаков существенен для атомов водорода: здесь электронная оболочка Н, и так состоявшая всего из одного электрона, оттянута к О атому, так что смять ее особенно легко. Смять электронную оболочку, скажем, О атома много труднее — вокруг ядра О вращается 8 "своих" электронов, да еще какую-то часть электронного облака атом О (в Н2О) оттягивает у соседних водородов.
Легкость проминания электронного облака у Н атома и превращает обычное электростатическое взаимодействие в водородную связь. Это относится ко всем водородным связям, из которых нас будут интересовать следующие, встречающиеся в белках связи: O—H::: O, N—H::: O, N—H::: N.
Итак, электронное облако при Н атоме — самое слабое, и оно сильно сминается при притяжении парциального положительного заряда Н к парциальному отрицательному заряду O (или N) атома. В результате ядро Н подходит к ядру О или N не на 2.35 — 2.75 (как то было бы при Вандерваальсовом взаимодействии, о котором мы говорили на прошлой лекции), а заметно ближе — на расстояние 1.8 — 2.1 (эти данные получены из кристаллов малых молекул).
При таком сближении и возникает водородная связь (или Н-связь). Н-атом (или, точнее, О-Н или N-Н группа) называется донором водородной связи, а тот О или N атом, к которому этот Н приближается, называется акцептором водородной связи.
Обратите внимание, что наблюдающееся в кристаллах при образовании Н-связи расстояние между О и/или N атомами донора и акцептора близко к 3.0 (например, во льду расстояние между ними равно 2.8 ). Это соответствует оптимальному Вандерваальсовому расстоянию между О и/или N атомами — т.е. наличие стоящего между ними Н атома не приводит к увеличению расстояния между донорным О (или N) и акцепторным О (или N) атомами: Н атом их не расталкивает, а связывает.
У каждой Н-связи один донор и один акцептор. При этом Н почти всегда выступает донором только одной Н-связи, а О может быть акцептором двух Н-связей. В последнем случае возникает "вилочковая" водородная связь.
Так как при образовании "вилочки" сильно сближаются два Н-атома (с зарядом + 1/3 каждый), то ее суммарная энергия меньше, чем удвоенная энергия одинарной (как на предыдущей схеме) Н-связи.
В отличие от Вандерваальсова взаимодействия, водородная связь весьма чувствительна к направлению — особенно к направлению донорной группы. Обычно валентная связь донора (N-H или О-Н) прямо смотрит на тот акцептор (О или N атом), с коим водородная связь образуется:
К ориентации акцепторной группировки водородная связь значительно менее чувствительна:
Энергия водородной связи составляет около 5 ккал/моль. Эта оценка базируется на сравнении экспериментальных теплот испарения сходных соединений, из которых одни могут завязывать водородные связи, а другие — нет. Например, теплота испарения диметилэфира — Н3С-О-СН3 — составляет около 5 ккал/моль, а теплота испарения спирта — СН3-СН2-ОН — около 10 ккал/моль. Эти вещества состоят из одних и тех же атомов — т.е. Вандерваальсовы взаимодействия в них практически одинаковы — но спирт может завязывать водородную связь, а диметилэфир — нет (у него нет О-Н группы!). Каждая ОН группа может быть донором только одной Н-связи, а ее О может такую связь акцептировать. Так как у каждой Н-связи должен быть один донор и акцептор, в спирте приходится по одной Н-связи на молекулу, т.е. цена одной водородной связи — около 10 ккал/моль - 5 ккал/моль = 5 ккал/моль.
Такая же оценка получается из теплоты испарения льда (680 кал/г = 680 кал/(1/18 моль) = 12 ккал/моль). Из них пара ккал/моль приходится на Вандерваальсовы взаимодействия — как видно из испарения малых молекул типа метана (СН4) или О2. На Н-связи остается около 10 ккал/моль. Во льду приходится по две водородных связи на молекулу Н2О, т.к. Н2О, со своими двумя ОН группами, может быть донором двух Н-связей (и столько же она может акцептировать своим О атомом). Значит, опять получается — примерно — (10 ккал/моль)/2 = 5 ккал/моль.
Рис.4-1. Нормальный лед. Пунктир — Н-связи. В ажурной структуре льда видны небольшие полости, окруженные молекулами Н2О. Картинка взята из [6].
Структура нормального льда диктуется Н-связями (Рис.4-1): она хороша для геометрии этих связей (О-Н смотрит прямо на О), но не очень хороша для плотного Вандерваальсового контакта молекул Н2О. Поэтому структура льда ажурна, в нем молекулы Н2О обволакивают микроскопические (размером меньше молекулы Н2О) поры. Ажурность структуры льда приводит к двум хорошо известным эффектам: (1) лед менее плотен, чем вода, он плавает в ней; и (2) под сильным давлением — например, лезвия конька — лед подплавляется.
Большинство из существующих во льду (Рис.4-1) водородных связей сохраняется и в жидкой воде. Это следует из малости теплоты плавления льда (80 кал/г) по сравнению с теплотой кипения воды (600 кал/г при 0оС). Можно было бы сказать, что в жидкой воде рвется только 80/(600+80) = 12% из существующих во льду Н-связей. Однако эта картина — что часть водородных связей в воде разорвана, а часть сохранена — неточна: скорее, все водородные связи в воде разбалтываются. Это хорошо иллюстрируется следующими экспериментальными данными.
На приведенном внизу Рисунке 4-2, кривая 1 соответствует максимуму инфракрасного спектра поглощения групп О-Н во льду (где все Н-связи завязаны); кривая 2 соответствует максимуму инфракрасного спектра поглощения групп О-Н отдельных молекул Н2О, растворенных в CCl4 (где Н-связей нет — раствор Н2О в CCl4 слишком разбавлен); а кривая 3 соответствует спектру поглощения жидкой воды. Если бы в жидкой воде было бы два сорта О-Н групп — образующие водородные связи и не образующие их — и одни О-Н группы в воде колебались бы так же (с той же частотой), как во льду (где они образуют Н-связи), а другие — как в окружении CCl4 (где они Н-связей не образуют). Тогда спектр воды имел бы два максимума, соответствующие двум состояниям О-Н групп, двум их характерным частотам колебаний: с какой частотой группа колеблется, с такой и поглощает свет. Но "двухмаксимумная" картина не наблюдается! Вместо нее на кривой 3 мы видим один, очень размытый максимум, простирающийся от максимума кривой 1 до максимума кривой 2. Это значит, что все О-Н группы в жидкой воде завязывают водородные связи — но все эти связи разболтаны, причем по-разному.
Это показывает, что картина, в которой часть водородных связей в воде разорвана, а часть сохранена, - строго говоря, неверна. Однако она столь проста и удобна для описания термодинамических свойств воды, что ею широко пользуются — и мы тоже будем к ней обращаться. Но надо иметь в виду, что она не точна.
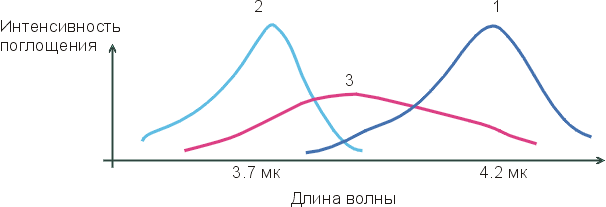
Рис.4-2. Характерный вид инфракрасных спектров поглощения О-Н групп во льду (1), в окружении CCl4 (2) и в жидкой воде (3).
Обратимся теперь к взаимодействию белковой цепи с водой.
Как и вода, остов белковой цепи полярен. Точнее — полярны входящие в остов пептидные группы. В целом остов белковой цепи имеет заряд 0, но распределение зарядов на его атомах (здесь опять заряд каждого атома выражен в долях от протонного заряда) выглядит так:
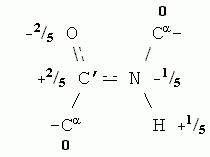
Парциальные заряды содержат и некоторые боковые группы, например, Ser (его боковая группа — -СН2-ОН — похожа на спирт). Еще более полярны заряженные аминокислотные остатки: заряд +1 присущ основаниям, входящим в боковые группы остатков Arg, Lys и His, когда они находятся в ионизованной форме (при примерно нейтральных рН), а у ионизованных кислотных боковых групп, Asp и Glu, заряд равен -1.
И пептидные группы главной цепи, и полярные боковые группы выступают донорами и акцепторами водородных связей. Они могут завязывать водородные связи друг с другом или с молекулами воды — и практически все они завязывают такие связи, так как энергия водородных связей — 5 ккал/моль — раз в десять превосходит энергию теплового движения, т.е. тепловое движение не может разрушить эти связи — разве что время от времени оно случайно нарушает малую часть из них.
Если внутримолекулярная связь между донором (D) и акцептором (А) водородной связи в белке завязывается в водном окружении, то эта связь замещает две водородные связи белка с молекулами воды (которые были до того, т.к. свято место пусто не бывает); и при этом еще создается одна связь между оторвавшимися молекулами воды:
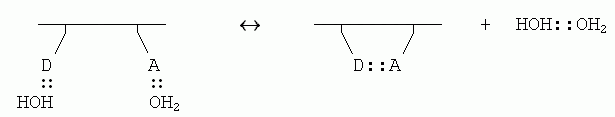
Энергетический баланс этой реакции близок к нулю: две Н-связи было, две стало. Однако энтропия воды возрастает, так как вода больше не привязана к белковой цепи и связанные Н-связью молекулы могут плавать где хочется (а энтропия именно и связана с множественностью состояний системы). При этом рост энтропии за счет освобождения димера воды от белка — примерно такой же, как рост энтропии при уходе молекулы Н2О изо льда в жидкую воду (в обоих случаях одна частица обретает свободу плавать).
Энтропийный эффект выхода молекулы Н2О изо льда в воду можно оценить следующим образом. Как известно, в точке плавления (для льда — при 0оС, т.е. при 273оК) энтропийный выигрыш от плавления как раз компенсирует энергетический проигрыш от него. А этот проигрыш нам известен: 80 кал/г, т.е. 80 Х 18 = 1440 кал/моль (18 - молекулярный вес Н2О).
Значит, вследствие роста энтропии свободная энергия системы "белок в воде" падает, — примерно на 1.5 килокалории на каждый моль формирующихся внутрибелковых водородных связей D:::A.
Эта выделенная водой свободная энергия может полностью или частично скомпенсировать рост свободной энергии, сопровождающий падение энтропии при фиксации групп D и А связью D:::A (раньше они болтались как хотели, а теперь, связанные, — не могут). Позже мы увидим, что падение свободной энергии воды примерно компенсирует энтропию необходимой для образования водородной связи (N-H:::O) фиксации мономера во вторичных структурах полипептидных цепей. В результате регулярная вторичная структура полипептидов в воде находится как раз на грани стабильности.
Итак, страшные слова — " энтропия " и " свободная энергия " — произнесены. Мой опыт показывает, что "энтропию" нормальный студент-биолог знает на слух (он слышал, что это — мера множественности состояний, мера беспорядка), а свободную энергию представляет совсем смутно... Так как нам понятие "свободная энергия" понадобится часто, я хочу уделить ей несколько минут сейчас, а потом, когда будет необходимо, поговорить о ней — и об энтропии — еще подробнее.
Начнем с простого примера: пусть молекула может находиться в двух состояниях, "а" и "б", например, — здесь, в этой комнате, на высоте 200 м от уровня моря ("а"), и в монастыре Далай-Ламы, в Гималаях, на высоте 5 км ("б"). Как соотносятся вероятности этих двух состояний — при условии, что мы следим за нашей молекулой так долго, что она успеет побывать и здесь, и там?
Обычно все помнят формулу Больцмана, которая гласит:
| Вероятность быть в состоянии с энергией Е пропорциональна exp(- E/kT). | (4.2) |
Физический смысл этой формулы заключается в том, что теплота окружающей среды (столкновения с другими молекулами) в определенной степени (в среднем — пропорционально температуре среды T) возбуждает нашу молекулу, и это позволяет ей забираться в область более или менее высоких энергий. Все это мы подробнее обсудим позже, а пока я позволю себе надеяться, что вы эту формулу помните. Напомню только, что k — это постоянная Больцмана, а T — абсолютная температура в градусах Кельвина.
Применительно к интересующему нас вопросу — как соотносятся вероятности пребывания молекулы на разных высотах — формула Больцмана сводится к барометрическому соотношению
| [Вероятность быть на высоте б] относится к [вероятности быть на высоте а] как exp(- E б/ kT) относится к exp(- E а/ kT), | (4.3) |
где E а — энергия молекулы в состоянии "а" (т.е. "здесь"), E б — в состоянии "б" ("на высоте 5 км"), а T — абсолютная температура (для простоты, будем считать, что с высотой она не меняется).
Из-за силы тяжести энергия молекулы "здесь" ниже, чем "на высоте 5 км"; так что, согласно Больцману, "на высоте 5 км" молекула будет проводить меньше времени, чем "здесь" [раза в полтора-два меньше; посчитайте сами при T =300oK, вспомнив, что E=mgh, где m — средняя масса молекулы воздуха (»30 дальтон = 30 г/моль), g»10м/с2 — ускорение свободного падения, h»5км — разность высот, а постоянная Больцмана k равна 1.38x10-23 Джоуля/градус (Дж = кгxм2/сек2 = 0.24 кал) в расчете на частицу, т.е. 2 кал/град в расчете на моль (6x10-23) частиц. Напомню, что R = 2 (кал/моль)/град. называется "газовой постоянной"].
То есть молекул на высоте в 5 км будет раза в два поменьше, чем здесь. Точнее — поменьше в равных единицах объема, например — внутри легких (в чем легко убедиться, попробовав подышать на разных высотах). Однако в сумме число молекул в монастыре Далай-Ламы больше, чем в этой комнате: его монастырь куда больше, чем наша комната. То есть там молекула может находиться в большем числе положений — для свободно летающей молекулы воздуха это число пропорционально объему помещения. Физики говорят в этом случае, что в том монастыре возможно куда больше микросостояний молекулы, чем в нашей комнате. Поэтому вероятность того, что наша молекула находится где-то в монастыре Далай-Ламы, относится к вероятности того, что она находится где-то в этой комнате, как
[ Вероятность где-то в объеме "б" ]: [ вероятность где-то в объеме "а" ] =
= [ V бexp(- E б/ kT)]: [ V аexp(- E а/ kT)]
Здесь V а — объем суммы состояний "а" ("нашей комнаты"), а V б — объем суммы состояний "б" ("его монастыря"). Вспомнив элементарную институтскую математику, а именно, что V можно представить как exp(ln V), эту формулу можно переписать как
[Вероятность где-то в объеме б]: [вероятность где-то в объеме а] =
= [exp(- E б/ kT + ln V б)]: [exp(- E а/ kT + ln V а)] =
= [exp(-(E б — T x k ln V б)/ kT)]: [exp(-(E а — T x k ln V а)/ kT)]
Последняя формула очень напоминает формулу (4.3), формулу Больцмана, но только она относится не к единице объема, а ко всему объему системы, и — внимание! — вместо энергий Е в ней стоят величины E — T x k ln V. Так вот, величина F = E — T x k ln V называется свободной энергией нашей молекулы воздуха при заданном объеме V и температуре T. А величина S = k ln V называется энтропией нашей молекулы в объеме V.
Это — в данном конкретном случае, когда "число доступных состояний" — это просто доступный для молекулы объем V (V а — "нашей комнаты", V б — "его монастыря").
В общем случае, энтропия S просто равна k x [ логарифм числа доступных состояний ]. А свободная энергия F связана с энергией Е, энтропией S и температурой Т системы согласно общей формуле
| F = E — TS | (4.4) |
Из двух состояний стабильнее, т.е. вероятнее то, у которого свободная энергия ниже:
| [Вероятность_где-то_в_объеме_"б"]: [вероятность_где-то_в_объеме_"а"] = = exp(- F б/ kT) : exp(- F а/ kT) = exp[-(F б- F а)/ kT ] | (4.5) |
Иными словами, более стабильному состоянию системы отвечает то, где ниже F, а самому стабильному состоянию системы (при заданной температуре и фиксированном объеме этой системы) отвечает минимум свободной энергии F.
Таким образом — "свободная энергия" — это естественное расширение обычного понятия "энергии" на случай, когда система обменивается теплом с окружающей средой. Напомню: если тело не обменивается теплом со средой, его стабильное состояние отвечает минимуму его энергии (или, проще: все, что может упасть — падает). А окружающее тепло делает стабильными определенные флуктуации, прыжки — такие, которые минимизируют свободную энергию тела. То есть приток тепла возбуждает молекулы системы, они начинают захватывать многочисленные состояния с более высокой энергией (т.е. их энтропия растет) — и, в результате, молекулы воздуха летают, а не падают на землю.
Спустимся, однако, с Гималаев к белкам.
Итак — каков же баланс энергий, энтропий и свободных энергий в разобранном нами примере образования водородной связи в белковой цепи? Для полной наглядности, сравним ход процесса в разных условиях:
Здесь EH < 0 - энергия Н-связи, а SH > 0 — энтропия перемещений и вращения свободного тела, т.е. свободной молекулы Н2О или свободного димера НОH::OH2. Водородные связи — воды с водой, воды с белком — стабильны, когда EH -TSH < 0 (а если EH -TSH > 0, т.е. если они нестабильны, — то есть в этом случае перед нами была бы уже не жидкая вода, а пар).
Сравнение приведенных выше схем показывает, что водородные связи в белковой цепи как бы становятся — за счет изменения энтропии связывающейся воды — менее стабильными в водном окружении, чем в вакууме; действительно, в водном окружении их свободная энергия есть Fб-Fа = -ТSH, — то есть она меньше, чем в вакууме, где Fб-Fа=EH.
Еще раз хочу подчеркнуть, что причина этого видимого ослабления — в том, что в водном окружении образовавшаяся внутри белковой цепи Н-связь замещает собой связь цепи с водой. И по той же причине водородные связи, стабилизующие структуру белка в воде носят энтропийную, а не энергетическую природу: энергии двух состояний цепи (с внутрицепочечной связью и без нее) примерно равны, и из этих двух состояний с примерно равной энергией стабильнее та, где выше энтропия, т.е. где больше число микросостояний. А их больше у оторванной молекулы воды, чем у связанной.
Обратите внимание: водородные связи в белковой цепи (в водном окружении) носят энтропийную, а не энергетическую природу именно потому, что энергия Н-связей очень высока: раз так, "свободные" от связей в белке доноры и акцепторы водородных связей в цепи всегда на деле не свободны от всех связей вообще, а связаны с водой. Оторвавшиеся же от белка — при образовании внутрибелковой Н-связи — молекулы Н2О тут же связываются друг с другом, так что энергия компенсируется, и свободно-энергетический выигрыш Н-связей в белке идет только от множественности возможных микросостояний оторвавшихся молекул воды. Правда, чтобы связаться друг с другом, молекулы Н2О должны пожертвовать часть своей обретенной свободы, часть энтропии — но лучше уж потерять небольшую энтропию, чем большую энергию!
То, что (1) молекулы воды сильно связаны друг с другом водородными связями; и (2) то, что эти связи образуются только при определенной взаимной ориентации молекул Н2О — определяет специфику воды как растворителя. Это приводит к разным интересным эффектам. Подробнее мы об этом поговорим в двух следующих лекциях.
Лекция 5
В первой части этой лекции я хочу продолжить разговор о термодинамике. Это нам пригодится, когда мы будем потом обсуждать специфику воды как растворителя. Свободная энергия погружения разных молекул в воду играет в этом обсуждении ключевую роль.
Для изучения свободной энергии погружения молекулы в воду берут закупоренную пробирку, наполовину заполненную водой и наполовину — паром, воздухом или органическим растворителем, и смотрят, как изучаемые молекулы распределились между этими двумя фазами.
Мы уже видели, что разность свободных энергий F определяет предпочтительное состояние рассматриваемой системы (в данном случае — предпочтительное местонахождение рассматриваемой частицы) — согласно формуле
| [Вероятность быть в б]:[вероятность быть в а] = exp[-(F б- F а)/ kT ] | (5.1) |
Свободная энергия F = E — TS складывается из энергии системы E и ее энтропии S. С энергией все, видимо, понятно. С температурой — понятно скорее интуитивно, и к ней мы еще вернемся. С энтропией — сложнее, и хочется повторить еще раз.
В простейшем случае частицы в сосуде, который мы, если вы помните, рассмотрели, S = k ln V, где V — доступный для частицы объем.
В чем смысл вхождения в свободную энергию этой энтропии (в виде члена -TS)? В том, что — если посмотреть на exp[ -F/kT ], забыв о E — то: exp[- (-TS) / kT ] = exp[-<
