Задача 1. Имеется следующая структурная модель:
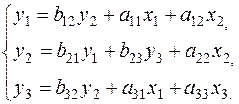
Соответствующая ей приведенная форма модели имеет вид:
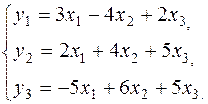
Определить, если это возможно, неизвестные параметры структурной модели.
Решение. Сначала определим идентифицируемость структурной модели. Ограничимся для простоты применением счетного правила. Приведем кратко информацию об этом правиле.
Обозначим Н – число эндогенных переменных в i - ом уравнении системы, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Тогда условие идентифицируемости уравнения может быть записано в виде следующего счетного правила:
D+1 = Н – уравнение идентифицируемо;
D+1 < Н – уравнение неидентифицируемо;
D+1 > Н – уравнение сверхидентифицируемо.
Первое и третье уравнения структурной модели имеют H = 2, D = 1. В первом уравнении две эндогенные переменные – y1, y2, в третьем тоже две – y2, y3; в обоих уравнениях не хватает по одной экзогенной переменной: в первом отсутствует х3, в третьем – х2. В этих уравнениях выполняется равенство D + 1 = H, и они идентифицируемы. Во втором уравнении присутствуют все три эндогенные переменные (H=3), а отсутствуют две экзогенные – х1 и х3 (D=2). Здесь также выполняется равенство D + 1 = H, и второе уравнение также идентифицируемо. Поскольку все три уравнения структурной модели идентифицируемы, система также идентифицируема.
Для идентифицируемых систем методом оценки структурных параметров является косвенный МНК. Он заключается в том, что уравнения приведенной формы модели (ПФМ), полученные обычным МНК как уравнения множественной регрессии, с помощью алгебраических преобразований превращаются в уравнения структурной формы модели (СФМ). Здесь, как видим, МНК применяется только один раз – для оценки коэффициентов приведенной формы.
Начнем с построения первого уравнения СФМ. Из всех уравнений ПФМ к нему ближе всех по структуре первое уравнение: в обоих уравнениях слева стоит y1, а справа стоят х1 и х2. Однако они отличаются тем, что в первом уравнении ПФМ стоит х3, а в первом уравнении СФМ стоит y2. Поэтому, чтобы получить первое уравнение СФМ из первого уравнения ПФМ, надо в последнем заменить х3 на выражение, в котором появилась бы y2. Эту замену делаем с помощью второго уравнения ПФМ:
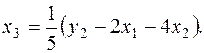
Подставим в первое уравнение ПФМ, получаем после элементарных преобразований:
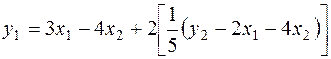 ,
,
или
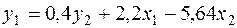 .
.
Это и есть первое уравнение СФМ.
Для получения третьего уравнения СФМ действуем аналогично: в третьем уравнении ПФМ заменяем х2 так, чтобы в результате замены появилась y2. такую замену снова делаем через второе уравнение ПФМ:
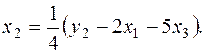 .
.
Подставим в третье уравнение ПФМ, получаем:
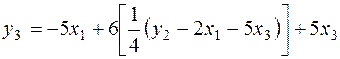 ,
,
или
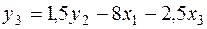 .
.
Это и есть третье уравнение СФМ.
Для получения второго уравнения СФМ требуются более сложные преобразования. Это связано с тем, что из второго уравнения ПФМ, как наиболее похожего на второе уравнение СФМ, надо исключить сразу две переменные – х1 и х3, чтобы при этом появились y1 и y3.. Последовательное исключение здесь не годится, их надо исключать одновременно. Для этого запишем первое и третье уравнения ПФМ как систему относительно исключаемых переменных:
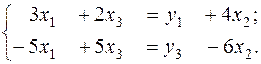
Решаем эту систему любым способом, например, например, методом определителей:
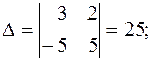
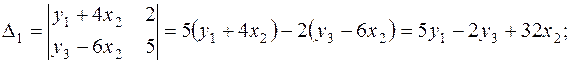
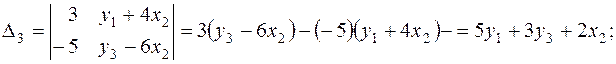
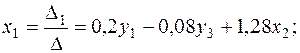
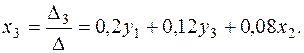
Подставим полученные решения во второе уравнение ПФМ, получаем второе уравнение СФМ:
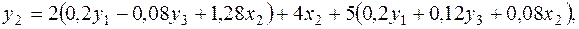
или
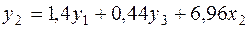 .
.
Теперь можем полностью записать структурную модель:
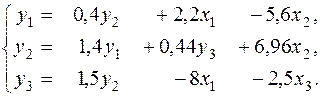
■






