IV. Векторная алгебра
4.1. Найдите расстояние между точками 
и 
. #
4.2. Найдите координаты середины отрезка 
, где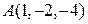 
, 
.
4.3. Найдите направляющие косинусы вектора 
.
.
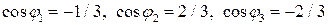4.4. Найдите углы наклона вектора 
к осям координат.
.
4.5. Найдите скалярное произведение векторов 
и 
, если известно, что 
, 
, а скалярное произведение 
.
4.6. В каком случае скалярное произведение двух векторов отрицательно?
Если угол между ними тупой.
4.7. Может ли скалярное произведение быть больше произведения длин векторов-сомножителей?
Нет, не может.
4.8. Найдите косинус угла между векторам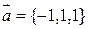и 
и 
.
4.9. Найдите проекцию вектора 
на направление вектора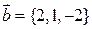 
.
–1
4.10. При каком значении 
векторы 
и 
ортогональны?
При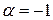 
.
4.11. При каких значениях и 
векторы и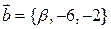 
будут коллинеарными?
При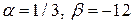 
.
4.12. Выясните, является тройка 
, 
и 
правой или левой.
Правой.
4.13. Найдите длину векторного произведения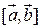 
, если , и их скалярное произведение равно 
4.14. Найдите площадь параллелограмма, построенного на векторах и .
4.15. При каком 
векторы 
, 
, 
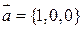будут компланарными.
При 
.
4.16. Найдите смешанное произведение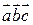 
векторов , , .
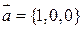4.17. Найдите объем треугольной пирамиды, построенной на векторах 
, , 
.
4.18. Найдите вектор, перпендикулярный векторам 
и 
, составляющий тупой угол с осью ординат и такой, что его длина равна 
.
# 
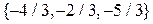
4.19. Найдите координаты вектора 
, где 
, 
.
# 
4.20. При каком 
векторы 
и 
перпендикулярны?
При 
.
4.21. Вычислите векторное произведение 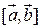, если 
и 
.
.
4.22. Даны векторы 
, 
и 
. Вычислите скалярное произведение 
.
4.23. Какой из приведенных ниже векторов ортогонален векторам 
и 
?
.
4.24. Вычислите углы треугольника 
с вершинами 
, 
и 
.
, 
, 
.
4.25. Упростите векторное произведение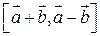 
.
4.26. Вектор 
, удовлетворяющий уравнению 
, равен…
… 
.
4.27. Вектор , удовлетворяющий уравнению 
, равен…
… 
.
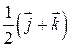4.28. Длина векторного произведения векторов 
и 
равна…
…3.
IV-а. Векторная алгебра
4-а.1. Скалярное произведение векторов равно произведению длин векторов-сомножителей, если …
# … угол между векторами равен нулю.
4-а.2. Векторы 
и 
перпендикулярны тогда и только тогда, когда …
# … длины векторов 
и 
равны.
4-а.3. Пусть 
и 
. Скалярное произведение 
. Тогда …
# … 
.
4-а.4. Даны точк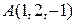и 
и 
. Тогда координаты вектора 
составляют …
# … 
4-а.5. Направляющие косинусы вектора 
равны …
# … 
.
4-а.6. Известно, что , 
, а скалярное произведение 
. Тогда скалярное произведение векторов и равно …
# … 3.
4-а.7. Скалярное произведение двух ненулевых векторов равно нулю, если …
# … если векторы взаимно перпендикулярны.
4-а.8. Косинус угла между векторами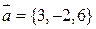 
и 
равен …
# … 
.
4-а.9. Проекция вектора 
на направление вектора 
равна …
# … 8.
4-а-.10. Пусть 
и 
. Тогда вектор 
имеет координаты …
# … 
.
4-а.11. Векторное произведение 
— это …
# … вектор, перпендикулярный векторам и .
4-а.12. В результате упрощения векторного произведения 
получим
# … 
.
4-а.13. Векторы 
, 
будут коллинеарны …
# … ни при каком .
4-а.14. При перестановке сомножителей в векторном произведении …
# … оно меняет знак.
4-а.15. Площадь треугольника равна 3. Тогда длина векторного произведения 
равна …
# … 6.
4-а.16. Пусть 
, 
, их скалярное произведение 
. Тогда длина векторного произведения 
равна …
# … 48.
4-а.17. Векторы 
и 
ортогональны при …
# … 
.
4-а.18. Смешанное произведение 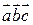трех взаимно перпендикулярных векторов …
# … равно произведению длин векторов-сомножителей, если тройка 
является левой.
4-а.19. Объем параллелепипеда, построенного на векторах , , , равен …
# … 6.
4-а.20. Даны векторы , и . Тогда векторное произведение 
равно # … 
.
-а.21. Длина векторного произведения векторов 
и 
равна …
# … 
.
4-а.22. Смешанное произведение векторов 
, 
и 
равно …
# … 39.
4-а.23. Вектор , удовлетворяющий уравнению 
, равен…
# … 
.
4-а.24. Векторы 
и 
перпендикулярны …
# … при .
4-а.25. Пусть скалярное произведение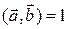 
, угол между векторами и равен 
. Тогда скалярный квадрат векторного произведения этих векторов
(т.е. 
) равен …
# …3.
V. Плоскость
5.1. Найдите, при каком значении 
плоскость 
будет перпендикулярна плоскости 
.
При 
.
5.2. Найдите, при каких и 
плоскости 
и 
параллельны?
При 
.
5.3. Найдите угол между плоскостью 
и координатной плоскостью 
.
5.4. Найдите расстояние от точки 
до плоскости .
5.5. Запишите уравнение плоскости, проходящей через точки 
, 
, 
.
5.6. Найдите плоскость, проходящую через точку 
и прямую пересечения плоскостей 
и 
.
5.7. Составьте уравнение плоскости, проходящей через точку 
параллельно плоскости 
.
.
.
5.8. Составьте уравнение плоскости, проходящей через точку 
перпендикулярно прямой 
, где 
и 
.
.
5.9. Составьте уравнение плоскости, проходящей через точки 
, 
и 
.
.
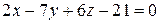5.10. Найдите угол между плоскостями 
и 
.
5.11. Составьте уравнение плоскости, проходящей через точку 
, если нормальный вектор этой плоскости 
.
.
5.12. Плоскость 
…
… параллельна оси 
.
5.13. Плоскость 
проходит через ось 
, если…
… 
.
Эта плоскость не может проходить через ось .
5.14. Составьте уравнение плоскости, проходящей через прямую 
параллельно вектору 
.
.
5.15. При каких и 
прямая 
лежит в плоскости 
?
.
5.16. Составьте уравнение плоскостей, делящих пополам двугранные углы, образованные плоскостями 
и 
.
и 
.
5.17. Найдите расстояние между плоскостями 
и 
.
5.18. Найдите объем пирамиды, образованной координатными плоскостями и плоскостью 
.
5.19. Найдите нормальный вектор плоскости, проходящей через начало координат и точки 
и 
.
.
5.20. Определите, как расположены точки 
и 
относительно плоскости 
.
По разные стороны от плоскости, причем точка по ту же сторону, что и начало координат.
5.21. Составьте уравнение плоскости, проходящей через середину отрезка перпендикулярно , если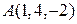 
, 
.
.
5.22. Установить, при каком значении плоскость 
будет параллельна плоскости 
?
Ни при каком.
5.23. Найдите расстояние от начала координат до плоскости 
.
5.24. Составьте уравнение плоскости, проходящей через начало координат параллельно векторам и 
.
.
5.25. Составьте уравнение плоскости, проходящей через точки 
, 
параллельно вектору .
.
5.26. При каком значении 
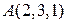точки 
, 
, 
и 
принадлежат одной плоскости?
При 
.
V-а. Плоскость
5-а.1. Плоскость 
будет перпендикулярна плоскости 
при …
# … 
.
5-а.2. Плоскости 
и 
параллельны при …
# … 
.
5-а.3. Расстояние от точки 
до плоскости 
равно…
# … 
.
5-а.4. Уравнение плоскости, проходящей через точки , 
, 
, имеет вид …
# … 
.
5-а.5. Уравнение плоскости, проходящей через точку 
параллельно плоскости 
, имеет вид …
# … 
.
5-а.6. Угол между плоскостями 
и 
равен …
# … 
.
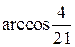5-а.7. Уравнение плоскости с нормальным вектором 
, проходящей через точку , имеет вид …
# … 
.
5-а.8. Плоскость 
проходит через ось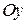 
, если…
# … 
и .
5-а.9. Уравнение плоскости, проходящей через прямую 
параллельно вектору 
, имеет вид …
# … 
.
5-а.10. Расстояние между плоскостями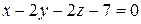 
и 
равно …
# … 
.
5-а.11. Объем пирамиды, образованной координатными плоскостями и плоскостью 
, равен …
# … 
.
5-а.12. Точки 
и 
расположены относительно плоскости 
…
# … по одну сторону, противоположную стороне, где лежит начало координат.
5-а.13. Уравнение плоскости, проходящей через начало координат параллельно векторам 
и 
, имеет вид …
# … 
.
5-а.14. Уравнение плоскости, проходящей через середину отрезка , где 
, 
, перпендикулярно этому отрезку, имеет вид …
# … 
.
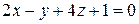5-а.15. Уравнение плоскости, проходящей через точку 
перпендикулярно вектору 
, имеет вид…
# … 
.
VI. Прямая в пространстве
6.1. Какой из указанных ниже векторов является направляющим вектором прямой 
?
.
6.2. Запишите канонические уравнения прямой, если ее параметрические уравнения имеют вид 
.
6.3. Запишите параметрические уравнения прямой 
.
6.4. При каком значении 
прямая 
будет перпендикулярна прямой 
При 
.
6.5. При каких значениях и 
прямые и 
параллельны?
При 
.
6.6. Установите взаимное расположение прямых 
и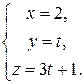 
Прямые скрещиваются.
6.7. При каких значениях и 
прямая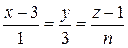 
и плоскость будут перпендикулярны?
При 
.
6.8. Найдите угол между прямой 
и плоскостью 
.
.
6.9. Установите взаимное расположение прямой 
и плоскости 
?
Прямая лежит в указанной плоскости.
6.10. Найдите расстояние от начала координат до прямой .
6.11. Найдите расстояние между прямыми 
и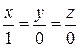 
.
6.12. Составьте канонические уравнения прямой, проходящей через точку 
перпендикулярно плоскости 
.
.
6.13. В какой точке прямая, проходящая через точки 
и 
, пересекает координатную плоскость 
?
6.14. Составьте уравнение плоскости, проходящей через точку перпендикулярно прямой 
.
6.15. Запишите канонические уравнения прямой 
.
6.16. Составьте параметрические уравнения перпендикуляра, проведенного через точку к плоскости 
.
.
6.17. При каком значении 
прямая 
параллельна плоскости 
?
При 
.
6.18. Составьте канонические уравнения прямой, проходящей через точку параллельно прямой 
.
6.19. При каком прямая 
пересекает ось ?
При 
.
6.20. Составьте параметрические уравнения прямой, проходящей через точки 
и .
.
6.21. Направляющим вектором прямой 
является вектор…
… 
.
6.22. Канонические уравнения оси ординат имеют вид…
… 
.
6.23. Параметрические уравнения медианы 
треугольника , где 
, , 
, имеют вид…
… 
6.24. Канонические уравнения прямой, делящей пополам угол между положительными направлениями осей и 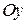, имеют вид…
… 
.
6.25. Направляющим вектором прямой 
служит вектор…
… 
.
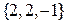VI-а. Прямая в пространстве
6-а.1. Направляющим вектором прямой 
является вектор с координатами
# … 
.
6-а.2. Направляющим вектором прямой 
является вектор с координатами …
#... .
6-а.3. Направляющим вектором прямой 
является вектор с координатами …
# … 
.
6-а.4. Направляющим вектором прямой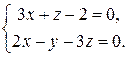 
является вектор с координатами …
# … 
.
6-а.5. Направляющим вектором прямой 
является вектор с координатами …
# … 
.
6-а.6. Направляющим вектором прямой 
является вектор с координатами …
# … 
.
6-а.7. Направляющим вектором прямой 
является вектор с координатами …
# … 
.
6-а.8. Каноническими уравнениями прямой 
являются …
# … 
.
6-а.9. Каноническими уравнениями прямой 
являются …
# … 
.
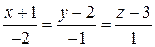6-а.10. Параметрическими уравнениями прямой 
являются…
# … .
6-а.11. Параметрическими уравнениями прямой 
являются …
# … .
6-а.12. Прямая 
принадлежит плоскости …
# … 
.
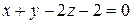6-а.13. Прямая 
принадлежит плоскости …
# … 
.
6-а.14. Прямая 
будет перпендикулярна прямой 
при …
# … 
.
6-а.15. Прямые 
и 
…
# … пересекаются.
6-а.16. Прямая 
перпендикулярна плоскости 
при …
# … 
.
6-а.17. Расстояние от точки до прямой 
равно …
# … 3.
6-а.18. Параметрические уравнения прямой, проходящей через точку 
перпендикулярно плоскости 
, имеют вид …
# … 
.
6-а.19. Прямая 
параллельна плоскости 
при …
# … 
.
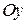6-а.20. Прямая пересекает ось при …
# … 
.
