Первое значение соответствует вероятности a = 0,05, второе - вероятности 0,01 и третье - вероятности 0,001, где n1 - число степеней свободы числителя, а n2 - число степеней свободы знаменателя.
 n1
n2 n1
n2
| ¥ | |||||||||
| 161,45 | 199,50 | 215,71 | 224,58 | 230,16 | 233,99 | 238,88 | 243,91 | 249,05 | 254,31 | |
| 4052,18 | 4999,50 | 5403,35 | 5624,58 | 5763,65 | 5858,99 | 5981,07 | 6106,32 | 6234,63 | 6365,68 | |
| 405284,07 | 499999,50 | 540379,20 | 562499,58 | 576404,56 | 585937,11 | 598144,16 | 610667,82 | 623497,46 | 636604,08 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 98,50 | 99,00 | 99,17 | 99,25 | 99,30 | 99,33 | 99,37 | 99,42 | 99,46 | 99,50 | |
| 998,50 | 999,00 | 999,17 | 999,25 | 999,30 | 999,33 | 999,37 | 999,42 | 999,46 | 999,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,85 | 8,74 | 8,64 | 8,53 | |
| 34,12 | 30,82 | 29,46 | 28,71 | 28,24 | 27,91 | 27,49 | 27,05 | 26,60 | 26,13 | |
| 167,03 | 148,50 | 141,11 | 137,10 | 134,58 | 132,85 | 130,62 | 128,32 | 125,93 | 123,47 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,80 | 14,37 | 13,93 | 13,46 | |
| 74,14 | 61,25 | 56,18 | 53,44 | 51,71 | 50,53 | 49,00 | 47,41 | 45,77 | 44,05 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 16,26 | 13,27 | 12,06 | 11,39 | 10,97 | 10,67 | 10,29 | 9,89 | 9,47 | 9,02 | |
| 47,18 | 37,12 | 33,20 | 31,09 | 29,75 | 28,83 | 27,65 | 26,42 | 25,13 | 23,79 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 13,75 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,10 | 7,72 | 7,31 | 6,88 | |
| 35,51 | 27,00 | 23,70 | 21,92 | 20,80 | 20,03 | 19,03 | 17,99 | 16,90 | 15,75 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 12,25 | 9,55 | 8,45 | 7,85 | 7,46 | 7,19 | 6,84 | 6,47 | 6,07 | 5,65 | |
| 29,25 | 21,69 | 18,77 | 17,20 | 16,21 | 15,52 | 14,63 | 13,71 | 12,73 | 11,70 |
Продолжение табл. 4
 n2 n1 n2 n1
| ¥ | |||||||||
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,03 | 5,67 | 5,28 | 4,86 | |
| 25,41 | 18,49 | 15,83 | 14,39 | 13,48 | 12,86 | 12,05 | 11,19 | 10,30 | 9,33 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,80 | 5,47 | 5,11 | 4,73 | 4,31 | |
| 22,86 | 16,39 | 13,90 | 12,56 | 11,71 | 11,13 | 10,37 | 9,57 | 8,72 | 7,81 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,06 | 4,71 | 4,33 | 3,91 | |
| 21,04 | 14,91 | 12,55 | 11,28 | 10,48 | 9,93 | 9,20 | 8,45 | 7,64 | 6,76 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 9,65 | 7,21 | 6,22 | 5,67 | 5,32 | 5,07 | 4,74 | 4,40 | 4,02 | 3,60 | |
| 19,69 | 13,81 | 11,56 | 10,35 | 9,58 | 9,05 | 8,35 | 7,63 | 6,85 | 6,00 | |
| 4,75 | 3,89 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,51 | 2,30 | |
| 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,50 | 4,16 | 3,78 | 3,36 | |
| 18,64 | 12,97 | 10,80 | 9,63 | 8,89 | 8,38 | 7,71 | 7,00 | 6,25 | 5,42 | |
| 4,67 | 3,81 | 3,41 | 3,18 | 3,03 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 9,07 | 6,70 | 5,74 | 5,21 | 4,86 | 4,62 | 4,30 | 3,96 | 3,59 | 3,17 | |
| 17,82 | 12,31 | 10,21 | 9,07 | 8,35 | 7,86 | 7,21 | 6,52 | 5,78 | 4,97 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 8,86 | 6,51 | 5,56 | 5,04 | 4,69 | 4,46 | 4,14 | 3,80 | 3,43 | 3,00 | |
| 17,14 | 11,78 | 9,73 | 8,62 | 7,92 | 7,44 | 6,80 | 6,13 | 5,41 | 4,60 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 8,68 | 6,36 | 5,42 | 4,89 | 4,56 | 4,32 | 4,00 | 3,67 | 3,29 | 2,87 | |
| 16,59 | 11,34 | 9,34 | 8,25 | 7,57 | 7,09 | 6,47 | 5,81 | 5,10 | 4,31 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,20 | 3,89 | 3,55 | 3,18 | 2,75 | |
| 16,12 | 10,97 | 9,01 | 7,94 | 7,27 | 6,80 | 6,19 | 5,55 | 4,85 | 4,06 |
Продолжение табл. 4
 n1
n2 n1
n2
| ¥ | |||||||||
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 8,40 | 6,11 | 5,18 | 4,67 | 4,34 | 4,10 | 3,79 | 3,46 | 3,08 | 2,65 | |
| 15,72 | 10,66 | 8,73 | 7,68 | 7,02 | 6,56 | 5,96 | 5,32 | 4,63 | 3,85 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 8,29 | 6,01 | 5,09 | 4,58 | 4,25 | 4,01 | 3,71 | 3,37 | 3,00 | 2,57 | |
| 15,38 | 10,39 | 8,49 | 7,46 | 6,81 | 6,35 | 5,76 | 5,13 | 4,45 | 3,67 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 8,18 | 5,93 | 5,01 | 4,50 | 4,17 | 3,94 | 3,63 | 3,30 | 2,92 | 2,49 | |
| 15,08 | 10,16 | 8,28 | 7,27 | 6,62 | 6,18 | 5,59 | 4,97 | 4,29 | 3,51 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 8,10 | 5,85 | 4,94 | 4,43 | 4,10 | 3,87 | 3,56 | 3,23 | 2,86 | 2,42 | |
| 14,82 | 9,95 | 8,10 | 7,10 | 6,46 | 6,02 | 5,44 | 4,82 | 4,15 | 3,38 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 8,02 | 5,78 | 4,87 | 4,37 | 4,04 | 3,81 | 3,51 | 3,17 | 2,80 | 2,36 | |
| 14,59 | 9,77 | 7,94 | 6,95 | 6,32 | 5,88 | 5,31 | 4,70 | 4,03 | 3,26 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 7,95 | 5,72 | 4,82 | 4,31 | 3,99 | 3,76 | 3,45 | 3,12 | 2,75 | 2,31 | |
| 14,38 | 9,61 | 7,80 | 6,81 | 6,19 | 5,76 | 5,19 | 4,58 | 3,92 | 3,15 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,37 | 2,20 | 2,01 | 1,76 | |
| 7,88 | 5,66 | 4,76 | 4,26 | 3,94 | 3,71 | 3,41 | 3,07 | 2,70 | 2,26 | |
| 14,20 | 9,47 | 7,67 | 6,70 | 6,08 | 5,65 | 5,09 | 4,48 | 3,82 | 3,05 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 7,82 | 5,61 | 4,72 | 4,22 | 3,90 | 3,67 | 3,36 | 3,03 | 2,66 | 2,21 | |
| 14,03 | 9,34 | 7,55 | 6,59 | 5,98 | 5,55 | 4,99 | 4,39 | 3,74 | 2,97 |
Окончание табл. 4
 n1
n2 n1
n2
| ¥ | |||||||||
| 4,24 | 3,39 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 7,77 | 5,57 | 4,68 | 4,18 | 3,85 | 3,63 | 3,32 | 2,99 | 2,62 | 2,17 | |
| 13,88 | 9,22 | 7,45 | 6,49 | 5,89 | 5,46 | 4,91 | 4,31 | 3,66 | 2,89 | |
| 4,23 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 7,72 | 5,53 | 4,64 | 4,14 | 3,82 | 3,59 | 3,29 | 2,96 | 2,58 | 2,13 | |
| 13,74 | 9,12 | 7,36 | 6,41 | 5,80 | 5,38 | 4,83 | 4,24 | 3,59 | 2,82 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,31 | 2,13 | 1,93 | 1,67 | |
| 7,68 | 5,49 | 4,60 | 4,11 | 3,78 | 3,56 | 3,26 | 2,93 | 2,55 | 2,10 | |
| 13,61 | 9,02 | 7,27 | 6,33 | 5,73 | 5,31 | 4,76 | 4,17 | 3,52 | 2,75 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,45 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 7,64 | 5,45 | 4,57 | 4,07 | 3,75 | 3,53 | 3,23 | 2,90 | 2,52 | 2,06 | |
| 13,50 | 8,93 | 7,19 | 6,25 | 5,66 | 5,24 | 4,69 | 4,11 | 3,46 | 2,69 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,55 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 7,60 | 5,42 | 4,54 | 4,04 | 3,73 | 3,50 | 3,20 | 2,87 | 2,49 | 2,03 | |
| 13,39 | 8,85 | 7,12 | 6,19 | 5,59 | 5,18 | 4,64 | 4,05 | 3,41 | 2,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 7,56 | 5,39 | 4,51 | 4,02 | 3,70 | 3,47 | 3,17 | 2,84 | 2,47 | 2,01 | |
| 13,29 | 8,77 | 7,05 | 6,12 | 5,53 | 5,12 | 4,58 | 4,00 | 3,36 | 2,59 | |
| 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 7,08 | 4,98 | 4,13 | 3,65 | 3,34 | 3,12 | 2,82 | 2,50 | 2,12 | 1,60 | |
| 11,97 | 7,77 | 6,17 | 5,31 | 4,76 | 4,37 | 3,86 | 3,32 | 2,69 | 1,89 | |
| ¥ | 3,84 | 3,00 | 2,60 | 2,37 | 2,21 | 2,10 | 1,94 | 1,75 | 1,52 | 1,03 |
| 6,63 | 4,61 | 3,78 | 3,32 | 3,02 | 2,80 | 2,51 | 2,18 | 1,79 | 1,04 | |
| 10,83 | 6,91 | 5,42 | 4,62 | 4,10 | 3,74 | 3,27 | 2,74 | 2,13 | 1,05 |
Таблица 5
Т а б л и ц а Ф и ш е р а - И е й т с а
Значения rкр, найденные для уровня значимости a и
чисел степеней свободы n = n - 2 в случае парной корреляции
и n = n - l - 2, где l - число исключенных величин в случае частной корреляции
| n | Двусторонние границы | n | Двусторонние границы | ||||||||
| 0,05 | 0,02 | 0,01 | 0,001 | 0,05 | 0,02 | 0,01 | 0,001 | ||||
| 0,997 | 1,000 | 1,000 | 1,000 | 0,468 | 0,543 | 0,590 | 0,708 | ||||
| 0,950 | 0,980 | 0,990 | 0,999 | 0,456 | 0,529 | 0,575 | 0,693 | ||||
| 0,878 | 0,934 | 0,959 | 0,991 | 0,444 | 0,516 | 0,561 | 0,679 | ||||
| 0,811 | 0,882 | 0,917 | 0,974 | 0,433 | 0,503 | 0,549 | 0,665 | ||||
| 0,754 | 0,833 | 0,875 | 0,951 | 0,423 | 0,492 | 0,537 | 0,652 | ||||
| 0,707 | 0,789 | 0,834 | 0,925 | 0,381 | 0,445 | 0,487 | 0,597 | ||||
| 0,666 | 0,750 | 0,798 | 0,898 | 0,349 | 0,409 | 0,449 | 0,554 | ||||
| 0,632 | 0,715 | 0,765 | 0,872 | 0,325 | 0,381 | 0,418 | 0,519 | ||||
| 0,602 | 0,685 | 0,735 | 0,847 | 0,304 | 0,358 | 0,393 | 0,490 | ||||
| 0,576 | 0,658 | 0,708 | 0,823 | 0,288 | 0,338 | 0,372 | 0,465 | ||||
| 0,553 | 0,634 | 0,684 | 0,801 | 0,273 | 0,322 | 0,354 | 0,443 | ||||
| 0,532 | 0,612 | 0,661 | 0,780 | 0,250 | 0,295 | 0,325 | 0,408 | ||||
| 0,514 | 0,592 | 0,641 | 0,760 | 0,232 | 0,274 | 0,302 | 0,380 | ||||
| 0,497 | 0,574 | 0,623 | 0,742 | 0,217 | 0,257 | 0,283 | 0,338 | ||||
| 0,482 | 0,558 | 0,606 | 0,725 | 0,205 | 0,242 | 0,267 | 0,338 | ||||
| 0,195 | 0,230 | 0,254 | 0,321 | ||||||||
| n | 0,025 | 0,01 | 0,005 | 0,0005 | n | 0,025 | 0,01 | 0,005 | 0,0005 | ||
| Односторонние границы | Односторонние границы |
Таблица 6
Т а б л и ц а Z - п р е о б р а з о в а н и я Ф и ш е р а

Значения
| Десятые доли r | Сотые (для последней строки тысячные) доли r | |||||||||
| 0,0 | 0,0000 | 0,0101 | 0,0200 | 0,0300 | 0,0400 | 0,0501 | 0,0601 | 0,0701 | 0,0802 | 0,0902 |
| 0,1 | 0,1003 | 0,1104 | 0,1206 | 0,1308 | 0,1409 | 0,1511 | 0,1614 | 0,1717 | 0,1820 | 0,1923 |
| 0,2 | 0,2027 | 0,2132 | 0,2237 | 0,2342 | 0,2448 | 0,2554 | 0,2661 | 0,2769 | 0,2877 | 0,2986 |
| 0,3 | 0,3095 | 0,3205 | 0,3316 | 0,3428 | 0,3541 | 0,3654 | 0,3767 | 0,3884 | 0,4001 | 0,4118 |
| 0,4 | 0,4236 | 0,4356 | 0,4477 | 0,4599 | 0,4722 | 0,4847 | 0,4973 | 0,5101 | 0,5230 | 0,5361 |
| 0,5 | 0,5493 | 0,5627 | 0,5764 | 0,5901 | 0,6042 | 0,6184 | 0,6328 | 0,6475 | 0,6625 | 0,6777 |
| 0,6 | 0,6932 | 0,7089 | 0,7250 | 0,7414 | 0,7582 | 0,7753 | 0,7928 | 0,8107 | 0,8291 | 0,8480 |
| 0,7 | 0,8673 | 0,8872 | 0,9077 | 0,9287 | 0,9505 | 0,9730 | 0,9962 | 1,0203 | 1,0454 | 1,0714 |
| 0,8 | 1,0986 | 1,1270 | 1,1568 | 1,1881 | 1,2212 | 1,2562 | 1,2933 | 1,3331 | 1,3758 | 1,4219 |
| 0,9 | 1,4722 | 1,5275 | 1,5890 | 1,6584 | 1,7381 | 1,8318 | 1,9459 | 2,0923 | 2,2976 | 2,6467 |
| 0,99 | 2,6466 | 2,6996 | 2,7587 | 2,8257 | 2,9031 | 2,9945 | 3,1063 | 3,2504 | 3,4534 | 3,8002 |
Таблица 7
Значение плотности вероятностей (функции Гаусса) 
для стандартного (нормированного) нормального закона распределения N(0,1) f(-t) = f(t)
| Целые и десятые доли t | Сотые доли t | |||||||||
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3726 | 0,3712 | 0,3697 |
| 0,4 | 0,3683 | 0,3668 | 0,3653 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3525 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2631 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1,0 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,3012 | 0,1989 | 0,1965 |
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0762 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
Окончание табл. 7
| Целые и десятые доли t | Сотые доли t | |||||||||
| 2,0 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,478 | 0,0568 | 0,0459 | 0,0449 |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0355 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 |
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
| 4,0 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 |
Таблица 8
Значение функции Пуассона 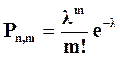
вероятности того, что в n испытаниях событие А наступит m раз
при вероятности наступления события p, близкой к нулю, и параметру λ=np
 l
m l
m
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 | 10,0 | ||
| 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,4966 | 0,4493 | 0,4066 | 0,3679 | 0,1353 | 0,0498 | 0,0183 | 0,0067 | 0,0025 | 0,0009 | 0,0003 | 0,0001 | 0,0001 | |||
| 0,0905 | 0,1637 | 0,2223 | 0,2681 | 0,3033 | 0,3293 | 0,3476 | 0,3595 | 0,3659 | 0,3679 | 0,2707 | 0,1494 | 0,0733 | 0,0337 | 0,0149 | 0,0064 | 0,0027 | 0,0011 | 0,0005 | |||
| 0,0045 | 0,0164 | 0,0333 | 0,0536 | 0,0758 | 0,0988 | 0,1216 | 0,1438 | 0,1547 | 0,1839 | 0.2707 | 0,2240 | 0,1465 | 0,0842 | 0,0446 | 0,0223 | 0,0107 | 0,0050 | 0,0023 | |||
| 0,0002 | 0,0011 | 0,0033 | 0,0072 | 0,0126 | 0,0198 | 0,0284 | 0,0383 | 0,0494 | 0,0613 | 0,1805 | 0,2240 | 0,1954 | 0,1404 | 0,0892 | 0,0521 | 0,0286 | 0,0150 | 0,0076 | |||
| 0,0000 | 0,0001 | 0,0003 | 0,0007 | 0,0016 | 0,0030 | 0,0050 | 0,0077 | 0,0111 | 0,0153 | 0,0902 | 0,1681 | 0,1954 | 0,1755 | 0,1339 | 0,0912 | 0,0572 | 0,0337 | 0,0189 | |||
| 0,0000 | 0,0000 | 0,0001 | 0,0002 | 0,0003 | 0,0007 | 0,0012 | 0,0020 | 0,0031 | 0,0361 | 0,1008 | 0,1563 | 0,1755 | 0,1606 | 0,1277 | 0,0916 | 0,0607 | 0,0378 | ||||
| 0,0000 | 0,0000 | 0,0000 | 0,0001 | 0,0002 | 0,0003 | 0,0005 | 0,0120 | 0,0504 | 0,1042 | 0,1462 | 0,1606 | 0,1490 | 0,1221 | 0,0911 | 0,0631 | ||||||
| 0,0000 | 0,0000 | 0,0000 | 0,0001 | 0,0034 | 0,0216 | 0,0595 | 0,1045 | 0,1377 | 0,1490 | 0,1396 | 0,1171 | 0,0901 | |||||||||
| 0,0000 | 0,0009 | 0,0081 | 0,0298 | 0,0653 | 0,1033 | 0,1304 | 0,1396 | 0,1318 | 0,1126 | ||||||||||||
| 0,0002 | 0,0027 | 0,0132 | 0,0363 | 0,0689 | 0,1014 | 0,1241 | 0,1318 | 0,1251 | |||||||||||||
| 0,0000 | 0,0008 | 0,0053 | 0,0181 | 0,0413 | 0,0710 | 0,0993 | 0,1186 | 0,1251 | |||||||||||||
| 0,0002 | 0,0019 | 0,0082 | 0,0225 | 0,0452 | 0,0722 | 0,0970 | 0,1137 | ||||||||||||||
| 0,0001 | 0,0006 | 0,0034 | 0,0113 | 0,0264 | 0,0481 | 0,0728 | 0,0948 | |||||||||||||
| 0,0000 | 0,0002 | 0,0013 | 0,0052 | 0,0142 | 0,0296 | 0,0504 | 0,0729 | ||||||||||||||
| 0,0001 | 0,0005 | 0,0022 | 0,0071 | 0,0169 | 0,0324 | 0,0521 | |||||||||||||||
| 0,0000 | 0,0002 | 0,0009 | 0,0033 | 0,0090 | 0,0194 | 0,0347 | |||||||||||||||
| 0,0000 | 0,0003 | 0,0015 | 0,0045 | 0,0109 | 0,0217 | ||||||||||||||||
| 0,0001 | 0,0006 | 0,0021 | 0,0058 | 0,0128 | |||||||||||||||||
| 0,0000 | 0,0002 | 0,0009 | 0,0029 | 0,0071 | |||||||||||||||||
| 0,0001 | 0,0004 | 0,0014 | 0,0037 |
Таблица 9
G - распределение
Пяти- и однопроцентное пределы для отношения G наибольшей выборочной дисперсии
к сумме k выборочных дисперсий, полученных из k независимых выборок объемом n.
Первое значение соответствует уровню значимости a = 0,05, а второе - a = 0,01
 u=n-1
k u=n-1
k
| ¥ | |||||||||||||
| 0,998 0,999 | 0,975 0,995 | 0,939 0,979 | 0,906 0,959 | 0,877 0,937 | 0,853 0,917 | 0,838 0,809 | 0,816 0,882 | 0,801 0,867 | 0,788 0,854 | 0,734 0,795 | 0,660 0,700 | 0,518 0,606 | 0,500 0,500 | |
| 0,967 0,993 | 0,871 0,942 | 0,798 0,883 | 0,746 0,834 | 0,707 0,903 | 0,677 0,761 | 0,653 0,734 | 0,633 0,711 | 0,617 0,691 | 0,603 0,674 | 0,547 0,606 | 0,475 0,515 | 0,403 0,423 | 0,333 0,333 | |
| 0,906 0,968 | 0,768 0,864 | 0,684 0,781 | 0,629 0,721 | 0,590 0,676 | 0,560 0,641 | 0,537 0,613 | 0,518 0,590 | 0,502 0,570 | 0,488 0,554 | 0,437 0,488 | 0,372 0,406 | 0,309 0,325 | 0,250 0,250 | |
| 0,841 0,928 | 0,684 0,789 | 0,598 0,696 | 0,544 0,633 | 0,507 0,588 | 0,478 0,553 | 0,456 0,526 | 0,439 0,504 | 0,424 0,485 | 0,412 0,470 | 0,365 0,409 | 0,307 0,335 | 0,251 0,254 | 0,200 0,200 | |
| 0,781 0,883 | 0,616 0,722 | 0,532 0,626 | 0,480 0,564 | 0,445 0,520 | 0,418 0,487 | 0,398 0,461 | 0,382 0,440 | 0,368 0,423 | 0,357 0,408 | 0,314 0,353 | 0,261 0,286 | 0,212 0,223 | 0,167 0,167 | |
| 0,727 0,838 | 0,561 0,664 | 0,480 0,569 | 0,431 0,508 | 0,397 0,466 | 0,373 0,435 | 0,354 0,411 | 0,338 0,391 | 0,326 0,375 | 0,315 0,362 | 0,276 0,311 | 0,228 0,249 | 0,183 0,193 | 0,143 0,143 | |
| 0,680 0,795 | 0,516 0,615 | 0,438 0,521 | 0,391 0,463 | 0,360 0,423 | 0,336 0,393 | 0,319 0,370 | 0,304 0,352 | 0,293 0,337 | 0,283 0,325 | 0,246 0,278 | 0,202 0,221 | 0,162 0,170 | 0,15 0,125 | |
| 0,639 0,754 | 0,478 0,573 | 0,403 0,481 | 0,358 0,425 | 0,329 0,387 | 0,307 0,359 | 0,290 0,338 | 0,277 0,321 | 0,266 0,307 | 0,257 0,295 | 0,223 0,251 | 0,182 0,199 | 0,145 0,152 | 0,111 0,111 |






