Сила трения.
Сила, возникающая в месте соприкосновения тел и препятствующая их относительному перемещению, называется силой трения. Направление силы трения противоположно направлению движения. Различают силу трения покоя и силу трения скольжения.
Сила трения всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Она всегда меньше силы нормального давления.
| 1. | Fтр = μ Fнорм |
Здесь:
Fтр — сила трения (Ньютон),
μ — коэффициент трения,
Fнорм — сила нормального давления, которое прижимает тело к опоре F (Ньютон)
11. Закон всемирного тяготения гласит:
Сила, с которой два тела притягиваются друг к другу, называется гравитационной силой (силой тяготения). Величина этой силы определяется законом всемирного тяготения, сформулированным Ньютоном.
| 1. | F = γ
|
Здесь:
F — гравитационная сила, с которой два тела притягиваются друг к другу (Ньютон),
m1 — масса первого тела (кг),
m2 — масса второго тела (кг),
r — расстояние между центрами масс тел (метр),
γ — гравитационная постоянная 6.67 · 10-11 (м3/(кг · сек2)),
Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:
12. Изучая механику твердого тела, мы использовали понятие абсолютно твердого тела. Но в природе не существует абсолютно твердых тел, т.к. все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.
Деформация называется упругой, если после того, как на тело перестали действовать внешние силы тело восстанавливает первоначальные размеры и форму. Деформации, сохраняющиеся в теле после прекращения действия внешних сил, называются пластическими (или остаточными)
РАБОТА И МОЩНОСТЬ
Работа силы.
Работа постоянной силы, действующей на прямолинейно движущееся тело
, где 
— перемещение тела, 
— сила, действующая на тело.
В общем случае, работа переменной силы, действующей на тело, движущееся по криволинейной траектории 
. Работа измеряется в Джоулях [Дж].
Работа момента сил, действующего на тело, вращающееся вокруг неподвижной оси 
, где 
— момент силы, 
— угол поворота.
В общем случае 
.
Совершенная нат телом работа переходит в его кинетическую энергию.
Мощность — это работа за единицу времени (1 с): 
. Мощность измеряется в Ваттах [Вт].
14. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательногодвижения.
Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:
— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы 
. Учитывая, что 
, Получим:
Если система замкнута, то есть 
, то 
, а величина
остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
где:
— масса тела
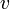— скорость центра масс тела
— момент инерции тела
— угловая скорость тела.
15. Потенциальная энергия 
— скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. 
16. Растяжение или сжатие пружины приводит к запасанию ее потенциальной энергии упругой деформации. Возвращение пружины к положению равновесия приводит к высвобождению запасенной энергии упругой деформации. Величина этой энергии равна:
Потенциальная энергия упругой деформации..
- работа силы упругости и изменение потенциальной энергии упругой деформации.
17. консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0
Диссипати́вные си́лы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту.
18. Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
§ mi — масса i -й точки,
§ ri — расстояние от i -й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
§ 
— масса малого элемента объёма тела 
,
§ 
— плотность,
§ 
— расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
19. Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. 
где — сила, действующая на частицу, а 
— радиус-вектор частицы.
Работа при вращательном движении. Момент силы
20.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
