7.1. Диэлектрические спектры
Под дисперсией понимают частотную зависимость диэлектрической проницаемости  . В широком диапазоне частот, обычно, наблюдается несколько областей дисперсии
. В широком диапазоне частот, обычно, наблюдается несколько областей дисперсии  , которые образуют диэлектрический спектр. Исследование дисперсии
, которые образуют диэлектрический спектр. Исследование дисперсии  - один из важных физических методов изучения свойств диэлектриков, позволяющих получить данные о характерных частотах
- один из важных физических методов изучения свойств диэлектриков, позволяющих получить данные о характерных частотах  и диэлектрических вкладах разных механизмов поляризации
и диэлектрических вкладах разных механизмов поляризации  .
.
На практике исследуются зависимости 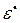 от частоты, температуры и внешнего поля. Измерения
от частоты, температуры и внешнего поля. Измерения  и
и  сложны. Только в диапазоне от 0.1 Гц до
сложны. Только в диапазоне от 0.1 Гц до  еще можно использовать эквивалентные схемы конденсатора, более высокочастотные диапазоны требуют СВЧ и оптических методов [3,6].
еще можно использовать эквивалентные схемы конденсатора, более высокочастотные диапазоны требуют СВЧ и оптических методов [3,6].
Спектр характеризуется рядом параметров:
- дисперсионная частота – соответствует максимуму  ;
;
- ширина спектра  - справа и слева от максимума при снижении
- справа и слева от максимума при снижении  в два раза отмечает точки на зависимости
в два раза отмечает точки на зависимости 
 и
и 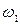 , тогда
, тогда 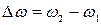 ;
;
- глубина дисперсии  определяется относительным вкладом в
определяется относительным вкладом в  того механизма поляризации, который выключается в процессе дисперсии, т.е. это параметр
того механизма поляризации, который выключается в процессе дисперсии, т.е. это параметр 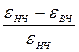 , где
, где  - диэлектрическая проницаемость при выключении данного механизма поляризации.
- диэлектрическая проницаемость при выключении данного механизма поляризации.
Математические закономерности дисперсии, исходя из простых моделей, мы установили в предыдущем разделе. Различают релаксационную дисперсию  , когда
, когда 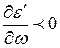 и
и  имеет пологий максимум и резонансную дисперсию, когда
имеет пологий максимум и резонансную дисперсию, когда 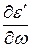 изменяет знак и
изменяет знак и  имеет острый максимум. Простые уравнения описывают эти два вида дисперсии – уравнение Дебая
имеет острый максимум. Простые уравнения описывают эти два вида дисперсии – уравнение Дебая
 (1)
(1)
и уравнение Друде – Лорентца
 . (2)
. (2)
Для анализа (1) и (2) их, обычно, видоизменяют, вводя «нормированные» по величине диэлектрического вклада обозначения.
Нормированное уравнение Дебая. Из (1) следует, что  , а
, а
 , обозначим
, обозначим
 (3)
(3)
или  , (4)
, (4)
где 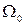 -дисперсионная частота, отвечающая максимуму поглощения. Уравнение (4) это есть нормированное уравнение Дебая.
-дисперсионная частота, отвечающая максимуму поглощения. Уравнение (4) это есть нормированное уравнение Дебая.
Нормированное уравнение Друде – Лорентца.
 . (5)
. (5)
В обоих уравнениях фигурирует  . Но разные механизмы поляризации связывают эту величину с частотой возбуждения.
. Но разные механизмы поляризации связывают эту величину с частотой возбуждения.
Если в диэлектрике в исследуемом диапазоне нет ни релаксационной, ни резонансной дисперсии, то  не зависит от
не зависит от  , а
, а 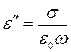 снижается с ростом частоты, следовательно,
снижается с ростом частоты, следовательно,
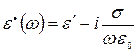 . (6)
. (6)
Итак, имеем три вида частотных зависимостей  , это (4),(5), (6).
, это (4),(5), (6).
На практике трудно определить, чем вызвана та или иная дисперсия. Это связано не только с особенностями поляризации диэлектриков, но и с погрешностями измерений  и
и  . Часто
. Часто  и
и  слабо изменяются с частотой в широком диапазоне частот, т.е. релаксационная поляризация приводит к размытому дисперсионному спектру, отвечающему наличию некоторого количества релаксаторов. Релаксаторы отличаются собственными частотами. Любое их распределение ведет к расширению области дисперсии
слабо изменяются с частотой в широком диапазоне частот, т.е. релаксационная поляризация приводит к размытому дисперсионному спектру, отвечающему наличию некоторого количества релаксаторов. Релаксаторы отличаются собственными частотами. Любое их распределение ведет к расширению области дисперсии  .
.
7.2.. Размытый релаксационный спектр
Определим основные параметры релаксационного спектра, описываемого уравнением (4). Разделяя действительную и мнимую части  имеем
имеем
 , (7)
, (7)
где  . Из (7) следует, что максимум
. Из (7) следует, что максимум  соответствует Х=1, т.е.
соответствует Х=1, т.е.  =0.5. Ширина спектра определяется параметром
=0.5. Ширина спектра определяется параметром  , где
, где 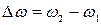 на уровне 0.5 от максимума
на уровне 0.5 от максимума  , т.е. при
, т.е. при  =0.25.Таким образом, при
=0.25.Таким образом, при  или
или  ширина спектра в случае одного вида релаксоров (спектр не размытый) составляет
ширина спектра в случае одного вида релаксоров (спектр не размытый) составляет 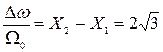 . Уравнение Дебая в координатах
. Уравнение Дебая в координатах  можно представить в таком виде
можно представить в таком виде
 . (8)
. (8)
Это выражение есть ни что иное, как уравнение окружности. На такую особенность уравнения Дебая впервые обратили внимание К.Коул и Р. Коул [3,5]. Диаграммы Коул – Коула в нормированных и обычных координатах выглядят так, как показано на рисунке 7.1. Когда дисперсия  хорошо описывается уравнением Дебая, экспериментальные точки ложатся на полуокружность. Если исследования проведены не во всем диапазоне частот, то диаграмма Коул – Коула позволяет провести аппроксимацию, что является несомненным достоинством методом диаграмм Коул – Коула. Если в диэлектрике могут протекать процессы поляризации с различным временем
хорошо описывается уравнением Дебая, экспериментальные точки ложатся на полуокружность. Если исследования проведены не во всем диапазоне частот, то диаграмма Коул – Коула позволяет провести аппроксимацию, что является несомненным достоинством методом диаграмм Коул – Коула. Если в диэлектрике могут протекать процессы поляризации с различным временем  ,
,

Рисунок 7.1. – Диаграммы Коул – Коула:
то диэлектрический спектр расширятся, что является следствием взаимодействия релаксирующих частиц. Для такого случая используется эмпирическое уравнение, которое в нормированном виде записывается следующим образом
 , (9)
, (9)
где 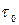 - средне время релаксации,
- средне время релаксации,
 - параметр, характеризующий распределение времени релаксации.
- параметр, характеризующий распределение времени релаксации.
Значение  находится по экспериментальным данным из построения диаграмм
находится по экспериментальным данным из построения диаграмм  . На диаграмме уравнение (9) описывает полуокружности, центр которых смещении вниз по оси
. На диаграмме уравнение (9) описывает полуокружности, центр которых смещении вниз по оси  на
на  , а радиус
, а радиус  , как показано на рисунке 7.1. Значение
, как показано на рисунке 7.1. Значение  определяется по величине угла между осью
определяется по величине угла между осью  и радиусом окружности. Параметр
и радиусом окружности. Параметр  - эмпирический и не имеет определенного молекулярного обоснования, тем не менее, метод Коул – Коула широко используется, когда времена релаксации сгруппированы симметрично относительно среднего значения
- эмпирический и не имеет определенного молекулярного обоснования, тем не менее, метод Коул – Коула широко используется, когда времена релаксации сгруппированы симметрично относительно среднего значения 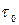 . Многочисленные эксперименты показывают, что релаксационный спектр дисперсии
. Многочисленные эксперименты показывают, что релаксационный спектр дисперсии  малочувствителен к распределению или взаимодействию релаксаторов, что объясняет почти универсальную возможность использования уравнения Дебая.
малочувствителен к распределению или взаимодействию релаксаторов, что объясняет почти универсальную возможность использования уравнения Дебая.
7.3. Размытый резонансный спектр
Частотная зависимость 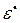 в диэлектриках в случае резонансной поляризации, обычно, описывается одним дисперсионным осциллятором с затуханием – уравнением Друде – Лорентца (5). Обозначим
в диэлектриках в случае резонансной поляризации, обычно, описывается одним дисперсионным осциллятором с затуханием – уравнением Друде – Лорентца (5). Обозначим  и, нормируя
и, нормируя  на величину диэлектрического вклада осциллятора
на величину диэлектрического вклада осциллятора  и после разделения
и после разделения  и
и  , из (5) при любом факторе потерь Г получим
, из (5) при любом факторе потерь Г получим
 . (10)
. (10)
Максимум и минимум функции  определяется так
определяется так
 при
при 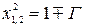 .
.
При 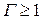 максимум функции
максимум функции  отсутствует, однако, минимум не исчезает при любых значениях Г. Этот минимум является отличительной особенностью резонансных спектров. Максимум
отсутствует, однако, минимум не исчезает при любых значениях Г. Этот минимум является отличительной особенностью резонансных спектров. Максимум 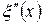 имеет место на частоте
имеет место на частоте
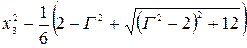 . (11)
. (11)
Из (11) следует, что только при  можно считать, что
можно считать, что  определяет истинную частоту осциллятора. Зависимости
определяет истинную частоту осциллятора. Зависимости  и
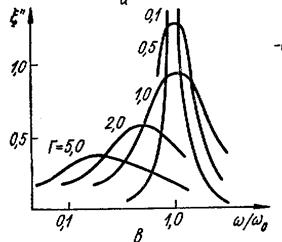
и 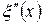 при разных значениях Г приведены на рисунке 7.2. Видно, как по мере роста затухания размываются как
при разных значениях Г приведены на рисунке 7.2. Видно, как по мере роста затухания размываются как  , так и
, так и 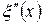 . Важной задачей исследования дисперсии
. Важной задачей исследования дисперсии  и обработки данных эксперимента является определение основных параметров уравнения Друде – Лорентца, т.е. величин
и обработки данных эксперимента является определение основных параметров уравнения Друде – Лорентца, т.е. величин  Первые два значения определяются из зависимости
Первые два значения определяются из зависимости  на тех частотах, где потери малы, т.е. вдали от резонансной частоты на низкой и высокой частотах. Определение
на тех частотах, где потери малы, т.е. вдали от резонансной частоты на низкой и высокой частотах. Определение  - более сложная задача. При малых затуханиях
- более сложная задача. При малых затуханиях  определяется по максимуму функции
определяется по максимуму функции 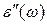 , а Г – по положению минимума зависимости
, а Г – по положению минимума зависимости  на некоторой частоте
на некоторой частоте  и известной частоте
и известной частоте  из соотношения
из соотношения 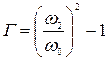 .
.

| 
|
Рисунок 7.2. - Частотная зависимость  и
и 
В заключение отметим, что релаксационные спектры, обычно, наблюдаются в низкочастотном диапазоне до частот порядка  , а резонансные – в инфракрасном и ультрафиолетовом диапазонах.
, а резонансные – в инфракрасном и ультрафиолетовом диапазонах.






