I. Наклонная, перпендикуляр, проекция.
-перпендикуляр, 
- основание перпендикуляра,
- наклонная, 
- проекция,
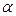- угол между прямой и плоскостью 
есть угол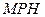 
между прямой и её проекцией на плоскость.
, 
.
1. Наклонная больше перпендикуляра, проведенного из той же точки.
2. Равные наклонные имеют равные проекции, и наоборот.
3. Из двух наклонных больше та, у которой больше проекция, и наоборот.
II. Расстояние от точки 
до плоскости , уравнение которой записано в общем виде 
равно 
.
Если многоугольник 
площади 
проектируется на плоскость в многоугольник 
площади 
, то площадь проекции вычисляется по формуле:
,
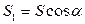где 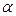- угол между плоскостями и .
I. Многогранники. Их вершины, ребра, грани, диагонали.
Многогранник есть пространственная фигура, ограниченная конечным числом плоских многоугольников. Вершины этих многоугольников называются вершинами многогранника, их ребра – ребрами многогранника. Диагональ многогранника есть отрезок, соединяющий две его вершины, не лежащие в одной грани.
II. Прямая и наклонная призма.
Многогранник называется призмой, если две его грани, называемые основаниями, есть равные многоугольники, а ребра, не лежащие в этих гранях, называемые боковыми ребрами, равны и параллельны.
, 
, где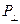 
- периметр перпендикулярного сечения.
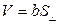- объём наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения.
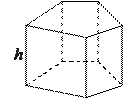Призма называется прямой, боковые ребра которой перпендикулярны плоскостям оснований.
;
.
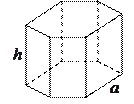Прямая призма называется правильной, если её основания есть правильные многоугольники.
;
;
.
III. Параллелепипед.
Параллелепипедом называется призма, основания которой – параллелограммы.
.
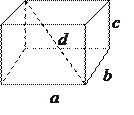Параллелепипед, у которого все грани – прямоугольники, называется прямоугольным.
; 
;
,
, 
, 
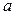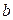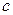- три измерения параллелепипеда, 
- диагональ.
IV. Куб.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
; 
.
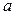- ребро куба.
V. Пирамида.
Пирамида есть многогранник, одна грань которого, называемая основанием, есть многоугольник, а остальные грани – треугольники, имеющие общую вершину, называемую вершиной пирамиды, не принадлежащую этому многоугольнику.
;
.
Треугольная пирамида называется тетраэдром.
,
где 
, 
, 
, 
- высоты, 
- радиус вписанного в тетраэдр шара.
Пирамида называется правильной, если её основание есть правильный многоугольник, а вершина проектируется в центр основания. Высота боковой грани правильной пирамиды называется апофемой.
, 
; ;
, 
- апофема.
Если все ребра треугольной (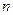
-угольной) пирамиды наклонены к основанию под одинаковым углом или все боковые ребра равны, то вершина пирамиды проектируется в центр окружности, описанной около основания.
Если все боковые грани треугольной пирамиды образуют равные двугранные углы с плоскостью основания, то высота пирамиды проектируется, либо в центр вписанной окружности, либо в центр одной из вневписанных окружностей основания.
VI. Усеченная пирамида.
, , 
-площади оснований.
Усеченная пирамида называется правильной, если её основания есть правильные многоугольники. Высота боковой грани правильной усеченной пирамиды называется апофемой.
,
, 
- периметры оснований, - апофема.
VII. Цилиндр.
; 
; 
;
,
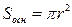- радиус основания, 
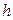- высота цилиндра.
VIII. Конус.
;
; 
;
,
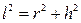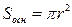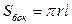- образующая, - радиус основания, 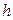- высота конуса.
; 
,
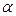- градусная мера кругового сектора развертки конуса.
IX. Усеченный конус.
;
;
;
.
X. Шар и сфера.
Поверхность шара называется сферой. 
;
;
.
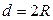XI. Шаровой сегмент.
- радиус основания сегмента;
;
;
.
XII. Шаровой сектор.
;
.
XIII. Шаровой слой.
;
;
,
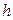- высота шарового слоя, 
, 
- радиусы оснований.
Библиография
1. Выгодский М.Я. Справочник по элементарной математике.
2. Атанасян Л.С. Геометрия 7-9, 10-11. Учебники для общеобразоват. учреждений.
3. Письменный Д.Т. Готовимся к экзамену по математике.
4. Сканави М.И. Сборник задач по математике для поступающих в вузы. Москва ОНИКС Мир и Образование, 2006.
5. Старков С.Н. Справочник по математическим формулам и графикам функций для студентов. – СПб.: Питер, 2009.
6. Шарыгин И.Ф. Стандарт по математике: 500 геометрических задач. Книга для учителя. Москва «Просвещение», 2007.
В авторской редакции.
Компьютерная вёрстка Шубовича А.А.
Подписано в печать Формат 
Усл. печ. л. 1,5. Тираж 100. Заказ
Издательско-полиграфический комплекс ВГСХА «Нива»
400002, Волгоград, Университетский пр-т, 26
