I. Векторы. Линейные операции над векторами.
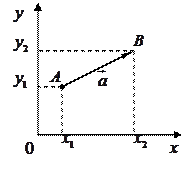
Вектор – это направленный отрезок.
- начало вектора, 
- конец вектора.
- вектор.
Координаты вектора: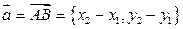 
.
Модуль вектора или его длина на плоскости равна расстоянию между точками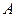 
и 
:
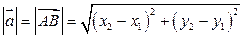или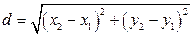 
.
Для вектора с координатами 
и 
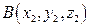в пространстве модуль вектора или его длина вычисляется по формуле:
.
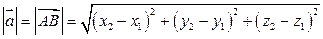Нулевым вектором 
называется вектор, модуль которого равен нулю. У него возможно любое направление в пространстве.
Радиус-вектором точки 
на плоскости называется вектор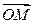 
, у которого начало совпадает с началом координат 
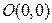. Координаты радиус-вектора совпадают с координатами его конца: 
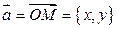. Модуль радиус-вектора или его длина:
.
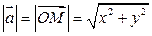Векторы можно складывать, вычитать, а также умножать вектор на число.
1. Вектор с координатами 
, называется противоположным вектору 
и обозначается 
.
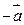2. Суммой двух векторов 
и 
на плоскости называется вектор, определяемый равенством:
.
Изображается диагональю параллелограмма, построенного на векторах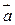 
и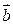 
с общим началом.
3. Суммой двух векторов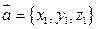 
и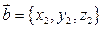 
в пространстве называется вектор, определяемый равенством:
.
4. Сложить два вектора 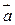и 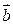можно двумя способами: по правилу треугольника и по правилу параллелограмма.
5. Разностью двух векторов 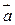и 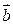на плоскости называется сумма вектора 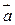с вектором, противоположным вектору 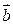. Координаты разности двух векторов находятся по правилу:
.
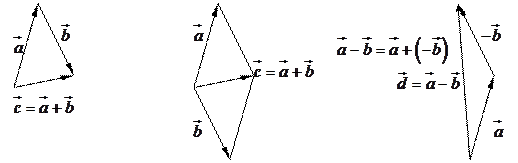
Свойства сложения векторов:
1. 
.
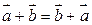2. 
.
3. 
.
4. 
.
Произведением вектора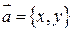 
на число 
называется вектор 
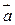. Это вектор, модуль которого в раз больше вектора , а направление совпадает с вектором 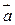, если 
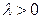, и противоположно 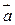, если 
.
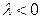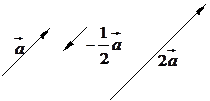Для данного вектора 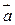построим векторы 
и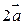 
:
Свойства умножения вектора на число:
1. 
, 
.
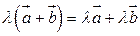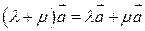2. 
.
3. 
.
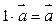II. Скалярное произведение векторов
|
Скалярным произведением 
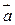двух векторов и 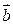называется произведение их модулей на косинус угла между ними:
,
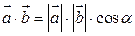где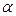 
- угол между векторам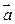и 
и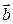 
.
Свойства скалярного произведения:
1. 
.
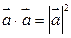2. 
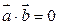, если 
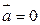, либо 
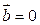, либо 
.
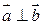3. 
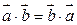(коммутативность).
4. 
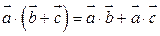(дистрибутивность).
5. 
.
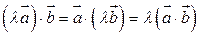6. Скалярные произведения осей координат: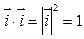 
, 
, 
, 
.
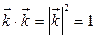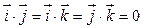7. Необходимое и достаточное (НИД) условие перпендикулярности двух векторов выражается равенством:
.
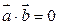Скалярное произведение векторов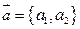 
и 
на плоскости может быть записано через координаты этих векторов:
.
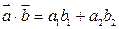Косинус угла между векторам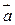и и 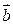на плоскости вычисляется по формуле:
.
Скалярное произведение векторов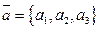 
и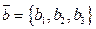 
в пространстве может быть записано через координаты этих векторов:
.
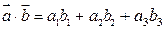Косинус угла между векторам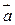и и 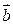в пространстве вычисляется по формуле:
.
III. Коллинеарные и компланарные векторы.
Векторы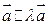 
параллельны между собой (коллинеарные). При этом один вектор выражается через другой.
У коллинеарных векторов соответствующие координаты пропорциональны. Т.е. если два вектора на плоскости 
и 
- коллинеарные, то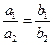 
.
Аналогично, если два вектора в пространстве 
и 
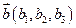- коллинеарные, то 
.
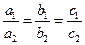Векторы 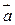и 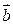называются линейно зависимыми, если 
(существуют) числа 
, 
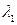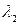, одновременно не равные нулю, т.ч. 
, т.е. если ненулевая линейная комбинация векторов, обращающаяся в ноль. Если равенство возможно только при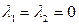 
, то векторы 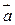и 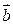называются линейно независимыми.
Два линейно зависимых вектора коллинеарные.
Три линейно зависимых вектора лежат в одной плоскости (или параллельны одной плоскости).
Векторы, лежащие в одной плоскости, называются компланарными.
Если векторы 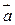и 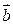линейно независимы, то любой вектор 
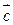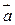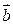, компланарный с и , может быть единственным образом разложен по этим векторам:
,
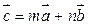где 
, 
- некоторые числа.
Если три вектора 
линейно независимы (т.е. не являются компланарными), то любой вектор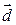 
может быть единственным образом разложен по этим векторам:
,
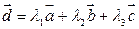где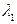 
, 
, 
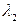- некоторые числа.
IV. Уравнение окружности.
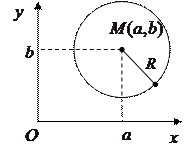
Уравнение окружности с центром в точке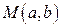 
и радиусом 
:
.
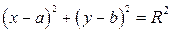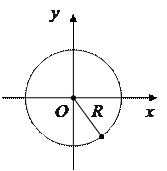
Уравнение окружности с центром в начале координат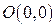 
и радиусом :
.
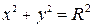V. Уравнение сферы.
Уравнение сферы с центром в точке 
и радиусом :
.
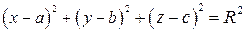Уравнение сферы с центром в начале координат 
и радиусом :
.
Стереометрия.
Принятые обозначения: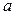 
- сторона основания правильного многогранника,
- число сторон основания,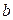 
- боковое ребро, 
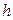- высота, 
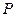- периметр основания, 
, 
, 
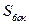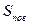- площади основания, боковой и полной поверхности многогранника;
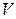- объём.
