Вища математика * ТАВРІЙСЬКИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ ВКАЗІВКИ
Для індивідуальної роботи студентів очної форми навчання
З вищої математики
ФАКУЛЬТЕТ ІКТ
спеціальність «Машинобудування»
«Ряди»
Частина 1
Мелітополь
Розробила: ст. викл. Богаєвська Н.В.
Методичні вказівки розглянуті й схвалені на засіданні кафедри
протокол № 10 від 12.05. 2009 р.
Рецензент: Омеляненко В.О.
Рекомендовані до видання методичною Радою факультету ІКТ
протокол № ______ від «______»______ 200 р.
І ЧИСЛОВІ РЯДИ
Основні поняття та означення
Розглянемо нескінченну послідовність чисел 
Означення 1. Вираз вигляду 
називається числовим рядом.
Приклади: а) 
б) 
Означення 2. Числа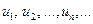 
називаються членами ряду, а вираз
- формулою загального члену ряду.
Означення 3. Сума n перших членів ряду називається n –ю частковою
сумою ряду.
Означення 4. Якщо існує границя часткової суми 
при 
, то ряд називається збіжним, а число 
- сумою ряду.
Приклад: Розглянемо геометричну прогресію
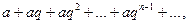де 
- знаменник прогресії.
Розглянемо 3 випадки:
а) 
тоді 
і
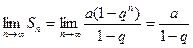
Отже, ряд є збіжним, його сума 
.
б) 
тоді 
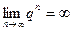і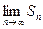 
- не існує.
Ряд розбігається.
в) 
і ряд є розбіжним;
тоді 
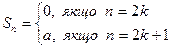і
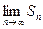- не існує, ряд розбігається.
Таким чином, геометрична прогресія 
збігається,
якщо 
, і розбігається, якщо 
Означення 5. Різниця між сумою S збіжного ряду і його частковою сумою Sn називається залишком ряду.
Залишок ряду також є числовим рядом.
Деякі властивості збіжних рядів
1. Якщо ряд 
збігається і має суму S, то ряд
також збігається і має суму 
.
2. Збіжні ряди можна почленно додавати або віднімати, тобто, якщо
то 
3. Відкидання будь-якого скінченого числа членів ряду не впливає на його збіжність або розбіжність, тобто, якщо ряд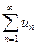 
є збіжним (розбіжним), то його залишок 
також є збіжним (розбіжним).
Встановити збіжність (розбіжність) ряду шляхом визначення Sn і обчислення 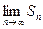можливо далеко не завжди через принципові труднощі
знаходження Sn. Простіше це можна зробити на основі ознак збіжності.
Необхідна ознака збіжності числового ряду
Розглянемо числовий ряд
(1)
Теорема. Якщо ряд (1) збіжний, то границя його загального члена при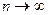 
дорівнює нулю, тобто 
Умова 
є тільки необхідною, але недостатньою умовою збіжності
ряду.
Наприклад, для гармонічного ряду 
, але можна
довести, що цей ряд є розбіжним.
Достатня умова розбіжності ряду
Якщо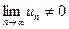 
ряд (1) є розбіжним.
Приклад. Дослідити ряд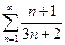 
на збіжність.
Розв’язання. Загальний член ряду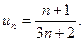 
Оскільки 
, то ряд є розбіжним.
Достатні ознаки збіжності
Ознаки порівняння.
Нехай маємо два ряди:
(1)
(2)
1) Якщо ряд (2) збігається, а члени ряду (1) не перевищують відповідних членів ряду (2), тобто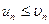 
то ряд (1) також збігається.
2) Якщо ряд (2) розбігається, а члени ряду (1) не менші за відповідні члени ряду (2), тобто 
, то ряд (1) також розбігається.
3) Якщо існує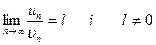 
, то ряди (1) і (2) є одночасно збіжними або розбіжними.
У якості рядів порівняння найчастіше беруть такі ряди:
а) Геометрична прогресія:
збігається, якщо 
розбігається, якщо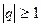 
.
б) Узагальнений гармонічний ряд або ряд Діріхле:
збігається, якщо 
;
розбігається, якщо 
.
Приклади. Дослідити ряди на збіжність:
1) 
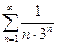
Розв’язання. Загальний член даного ряду
Ряд порівняння 
- геометрична прогресія.
Оскільки 
і ряд є збіжним 
, то даний ряд збігається.
2) 
Розв’язання. 
. Ряд порівняння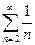 
- гармонічний ряд.
, оскільки 
і гармонічний ряд розбігається, то даний ряд є розбіжним.
3) 
Розв’язання. 
Ряд порівняння отримуємо, залишаючи в чисельнику і знаменнику загального члену лише найвищі степені n: 
.
Отже, ряд порівняння 
- це є збіжний ряд Діріхле, оскільки 
.
Знайдемо 
Оскільки ряд порівняння є збіжним, то даний ряд також збігається.
Завдання для самостійної роботи
І.Довести розбіжність рядів.
ІІ. Дослідити ряди на збіжність за допомогою ознак порівняння.
Ознака Даламбера
Розглянемо ряд з додатними членами:
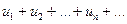(1)
Якщо існує границя 
, то:
1) ряд збігається, якщо l < 1;
2) ряд розбігається, якщо l >1;
3) якщо l = 1, то ознака не дає відповіді на питання про збіжність ряду (треба використати інші достатні ознаки збіжності).
Примітка. Якщо 
, то ряд (1) є розбіжним.
Приклади. Дослідити ряди на збіжність:
1) 
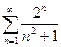
Розв’язання., складаємо.
Знаходимо 
Отже, даний ряд є розбіжним.
2) 
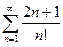
Розв’язання.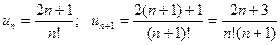 
(за означенням 
).
Знаходимо: 
,
отже, ряд є збіжним.
(Невизначеність вигляду 
було розкрито за допомогою правила Лопіталя).
3) 
.
Розв’язання. 
Знаходимо: 
,
оскільки це є друга визначна границя.
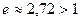, тому ряд є розбіжним.
Зауваження. Ознаку Даламбера доцільно застосовувати в тому випадку, коли загальний член ряду містить множники вигляду 
або 
.
Завдання для самостійної роботи
За допомогою ознаки Даламбера дослідити ряди на збіжність.
У прикладі 4: 
Радикальна ознака Коші
