Задача 1
Даны вершины А (5; 3), В (-11; -9), С (-4; 15) треугольника АВС. Требуется найти:
а) уравнения сторон треугольника АВ, АС и ВС;
б) уравнения высот АL, BH и СK;
в) длины высот;
г) величины углов (в градусах, минутах и радианах);
д) уравнение биссектрисы BS;
Е) уравнение медианы СМ.
Решение:
а) Найдём уравнения сторон:
Уравнение стороны AВ или уравнение прямой проходящей через точки A (xA; yA) и В (xB; yB), имеет вид: 
Подставив в эту формулу координаты точек A и B, получаем:
3 х -4 у -3=0 – общее уравнение прямой (стороны) AB.
у= – уравнение прямой (стороны) AB с угловым коэффициентом.
| Уравнение стороны AС или уравнение прямой проходящей через точки A (xA; yA) и С (xC; yC), имеет вид: 
Подставив в эту формулу координаты точек A и С, получаем:
4 х +3 у -29=0 – общее уравнение прямой (стороны) AС.
у= – уравнение прямой (стороны) AС с угловым коэффициентом.
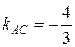
| Уравнение стороны BС или уравнение прямой проходящей через точки В (xB; yB) и С (xC; yC), имеет вид: 
Подставив в эту формулу координаты точек B и С, получаем:
24 х -7 у +201=0 – общее уравнение прямой (стороны) BС.
у= – уравнение прямой (стороны) BС с угловым коэффициентом.
|
б) Найдём уравнения высот:
определим сначала угловые коэффициенты высот:
AL ^ BС Þ kAL · kBC =-1
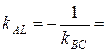
| ВH ^ AС Þ kBH · kAC =-1
|
найдём уравнения высот:
| найдём уравнение высоты AL, как уравнение прямой, проходящей через точку A (xA; yA) в заданном угловым коэффициентом kAL направлении: у - уА = kАL (х - хА) 7 х +24 у -107=0 – общее уравнение прямой (высоты) AL. | найдём уравнение высоты BH, как уравнение прямой, проходящей через точку B (xB; yB) в заданном угловым коэффициентом kBH направлении: у - уB = kBH (х - хB) 3 х -4 у -3=0 – общее уравнение прямой (высоты) BH. | найдём уравнение высоты CK, как уравнение прямой, проходящей через точку _______ в заданном угловым коэффициентом ____ направлении: ____________ – общее уравнение прямой (высоты) CK. |
в) Найдём длины высот:
I способ:
Нахождение расстояния от точки до прямой
Пусть заданы прямая l: Ах+Ву+С= 0, и точка М (х 0; у 0), тогда расстояние d от точки М до прямой l находится по формуле:
найдём | AL |, как расстояние от точки A (5; 3) до прямой ВС: 24 х -7 у +201=0
| найдём | BH |, как расстояние от точки B (-11; -9) до прямой AС: 4 х +3 у -29=0 | найдём | CK |, как расстояние от точки C (-4; 15) до прямой AB: 3 х -4 у -3=0 |
II способ:
Нахождение основания перпендикуляра, а затем вычисление длины высоты, как расстояния между двумя точками
| Вычислим координаты точки L: L = AL Ç ВС | Вычислим координаты точки Н: Н = BH Ç АС | Вычислим координаты точки К: K = CK Ç АВ |
Итак, L (;)
|
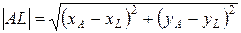
Строим чертёж:
| y | ||||||||||||||||||||||||||||||||
| x | ||||||||||||||||||||||||||||||||
г) Найдём величины углов:
I способ:
Нахождение тангенса угла между прямыми заданными угловыми коэффициентами
угол j,на который надо повернуть в положительном направлении прямую l 1вокруг точки их пересечения до совпадения с прямой l 2 находится по формуле:
Найдём величину угла А:
| Найдём величину угла В:
| Найдём величину угла С:
|
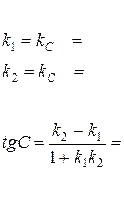
II способ:
Нахождение косинуса угла между векторами (средствами векторной алгебры):
 
|
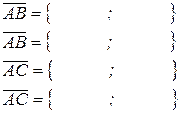
д) Найдём уравнения биссектрис:
Для определения уравнения биссектрисы угла воспользуемся уравнениями двух прямых, образовавших этот угол, А 1 х + В 1 у + С 1=0 и А 2 х + В 2 у + С 2=0, тогда уравнения таких биссектрис имеют вид:
уравнения биссектрисы угла В
АВ: 3 х -4 у -3=0
ВС: 24 х -7 у +201=0
Уравнения двух биссектрис угла В (внутреннего и внешнего) имеют вид:
Искомый угловой коэффициент должен удовлетворять неравенству: kBA < kBS < kBC,
так как kBA =0,75, kBС =24/7, то kBS =13/9
и уравнение биссектрисы ВS имеет вид: 13 х -9 у +62=0.
|
е) Найдём уравнения медиан:
медиана СМ, где М — середина АВ
М (;)
| |
| Уравнение медианы СМ |
Задача 2.
Пусть точка А (-3; 2) - вершина квадрата ABCD, а его диагональ BD расположена на прямой х +3 у -13=0. Найдите:
а) координаты вершин B, C и D;
