Байкальский государственный университет

Министерство образования и науки

Читинский институт (филиал) ФГБОУ ВПО

Байкальский государственный университет

экономики и права»

 

 

Кафедра математики

 

 

Контрольная работа по темам

«Математический анализ»,

«Элементы теории вероятностей»

 

для студентов 1-го курса

направлений ГМУ, МО, УП, ТД

3 триместр

Раздел «Производная»

Задача 1. Найти производную.

 

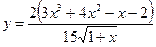
1.	2.
3.	4.
5.	6.
7.	8.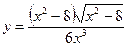
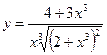
9.	10.
11.	12.
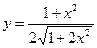
13.	14.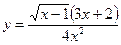
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.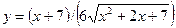
27.	28.
29.	30.
31.

 

Задача 2. Найти производную.

1.	2.
3.	4.
5.	6.
7.	8.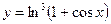
9.	10.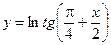
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
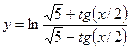
27.	28.
29.	30.
31.

 

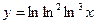
Задача 3. Найти производную.

1.	2.
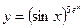
3.	4.
5.	6.
7.	8.
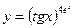
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.
31.

 

Задача 4. Найти наибольшее и наименьшее значение функций на заданных отрезках.

1.	2.
3.	4.
5.	6.
7.	8.
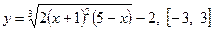
9.	10.
11.	12.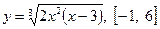
13.	14.
15.	16.
17.	18.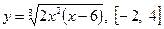
19.	20.
21.	22.
23.	24.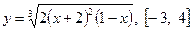
25.	26.
27.	28.
29.	30.
31.

 

 

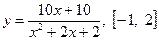
Задача 5. Провести полное исследование функций и построить их графики.

1.	2.
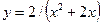
3.	4.
5.	6.
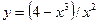
7.	8.
9.	10.
11.	12.
13.	14.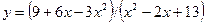
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.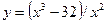
27.	28.
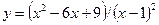
29.	30.
31.

 

Раздел «Интегралы»

Задача 6. Найти неопределённые интегралы.

1.	2.
3.	4.
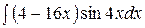
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.
31.

Задача 7. Найти неопределённые интегралы.

 

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.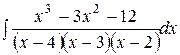
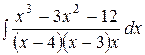
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.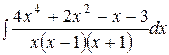
25.	26.
27.	28.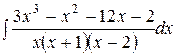
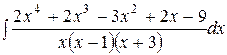
29.	30.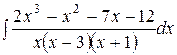
31.

 

Задача 8. Вычислить определённые интегралы.

 

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
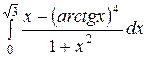
13.	14.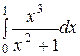
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.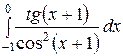
25.	26.
27.	28.
29.	30.
31.

 

Задача 9. Вычислить определённые интегралы.

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
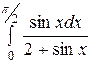
29.	30.
31.

 

Раздел «Дифференциальные уравнения»

 

Задача 10. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде ).

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.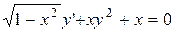
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.
31.

 

Задача 11. Найти общий интеграл дифференциального уравнения.

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.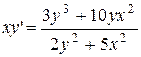
19.	20.
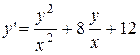
21.	22.
23.	24.
25.	26.
27.	28.
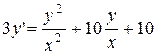
29.	30.
31.

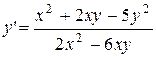
Раздел «Элементы теории вероятностей»

Задача 12

1. Имеются две одинаковые урны. В первой - семь белых шаров и три черных, а во второй - шесть белых и четыре черных. Наудачу выбирается урна и из нее наугад извлекается один шар. Какова вероятность того, что шар оказался белым?

2. Имеются три одинаковые урны. В первой урне находится 4 белых и 6 черных шаров, во второй - белые и в третьей - только черные. Наудачу выбирается урна и из нее наугад извлекается один шар. Какова вероятность того, что этот шар черный?

3. В сборной по гимнастике 24 % мастеров спорта, 40 % кандидатов в мастера и 36 % перворазрядников. Вероятность того, что мастер спорта или кандидат в мастера выполнит упражнения на “ отлично “, равна 0,9. Для перворазрядника эта вероятность равна 0, 6. Определить вероятность того, что член команды, подошедший к снаряду, выполнит упражнение на “отлично”.

4. Первый цех изготовил 50 лампочек, второй - 30, третий - 20. Вероятность того, что лампочка стандартная, для первого цеха равна 0,8, для второго - 0,7 и для третьего - 0,9. Из партии наугад взята одна лампочка. Определить вероятность того, что она стандартная.

5. В ящике содержится 12 деталей, изготовленных заводом N1, 20 деталей - заводом N 2 и 18 - заводом N 3. Вероятность того, что деталь, изготовленная заводами N1, N2, N3, отличного качества и соответственно равна 0,9; 0,6; 0,9. Найти вероятность того, что наудачу извлеченная из ящика деталь отличного качества.

6. В специализированную больницу поступают в среднем 50 % больных с заболеванием К, 30 % с заболеванием В, 20 % с заболеванием С. Вероятность полного излечения болезни К равна 0,7 для болезней В и С эти вероятности соответственно равны 0,8 и 0,9. Найти вероятность того, что наудачу взятый больной будет полностью излечен.

7. Один из трех охотников стреляет по волку. Вероятность попадания для каждого из них соответственно равна 0,2; 0,4; 0,6. Найти вероятность того, что пуля попадет в волка.

8. В правом кармане имеются три монеты по 20 коп. и четыре - по 3 коп., а в левом - шесть монет по 20 коп. и три - по 3 коп. Из правого кармана наудачу перекладывают пять монет в левый карман. Определить вероятность того, что после этого произвольная монета, вынутая из левого кармана, будет двадцати копеечная.

9. Из 10 шаров первой урны - 8 белых, а из 20 шаров второй урны - 4 белых. Из каждой урны наудачу извлекают по одному шару, а из них наудачу берут один. Найти вероятность того, что взят белый шар.

10. Для контроля за качеством продукции из трех партий деталей взято для проверки одна деталь. Как велика вероятность обнаружения брака, если в одной партии 2/3 деталей бракованные, а в двух других - все детали стандартные.

11. Прибор может работать в двух режимах - нормальном и перегрузочном. Нормальный режим наблюдается в 80 % времени, а перегрузочный в 20 %. Вероятность выхода прибора из строя в нормальном режиме равна 0,1, а при перегрузке - 0,7. Найти вероятность выхода прибора из строя.

12. В тире имеется три ружья, вероятности попадания из которых соответственно равны 0,5; 0,6; 0,7. Определить вероятность попадания при одном выстреле, если стреляющий берет наугад одно из ружей?

13. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность попадания в цель из винтовки с оптическим прицелом равна 0,95, а из винтовки без такого прицела - 0,7. Из наудачу взятой винтовки произведен выстрел. Какова вероятность попадания?

14. Приборы одного наименования изготовляются двумя заводами. Первый завод поставляет 2/3 всех приборов, поступающих на производство, а второй - 1/3. Вероятность безотказной работы (надежность) прибора, изготовленного первым заводом, равна 0,93; второго - 0,87. Определить надежность (вероятность безотказной работы) прибора, поступающего на производство.

15. В вычислительной лаборатории имеется 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Найти вероятность того, что до окончания расчета машина не выйдет из строя, если выбрана она наугад.

16. В маршрутном такси едут три пассажира. Каждый, из которых на следующей остановке может выйти с вероятностью 0,7; кроме того, в такси с вероятностью 0,4 не входит ни один новый пассажир. Найти вероятность того, что, когда такси снова тронется в путь после остановки, в нем по-прежнему будет три пассажира.

17. В первой коробке из 20 карандашей - 15 красных; во второй из 30 карандашей - 24 красных, а в третьей из 10 карандашей - 6 красных. Найти вероятность того, что наудачу извлеченный карандаш из наудачу выбранной коробки - красный.

18. Сборщик получил три коробки деталей, изготовленных заводом №1 и 2 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 - стандартна, равна 0,8, а для завода №2 - 0,9. Сборщик наудачу извлек деталь из наудачу выбранной коробки. Найти вероятность того, что извлеченная деталь стандартная.

19. Имеются две урны. В первой - 6 белых и 4 черных; во второй 8 белых и 12 черных; из первой урны наугад перекладывают один шар во вторую. После этого из второй урны наугад извлекают один шар. Найти вероятность того, что этот шар будет белым.

20. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго - 0,03, для третьего - 0,04. Обрабатываемые детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего - в два раза меньше, чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной.

21. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника - 0,9; для велосипедиста - 0,8; для бегуна - 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит квалификационную норму по своему виду спорта.

22. В телеателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, равна 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок.

23. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,3 % брака, второй - 0,2 % и третий - 0,4 %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго - 2000 и с третьего - 2500 деталей.

24. В студенческой группе из 30 человек 20 занимаются лыжным спортом, 6 - легкой атлетикой и 4 - гимнастикой. Вероятность выполнить норму первого разряда такова: для лыжников - 0,9; для легкоатлетов - 0,8; для гимнастов - 0,75. Найти вероятность того, что студент, выбранный наудачу, выполнит норму первого разряда по своему виду спорта.

25. В первом ящике содержится 12 радиоламп, из них одна - нестандартная; во втором - 10 радиоламп, из которых также одна нестандартная. Из первого во второй ящик наугад перекладывают одну лампу, после чего из второго извлекают одну лампу. Найти вероятность того, что она нестандартна.

26. На одном заводе на каждые 100 лампочек приходится в среднем 10 нестандартных, на втором - 15, на третьем - 20. Продукция этих заводов составляет соответственно 50, 30 и 20 % всех электролампочек, приобретаемых жителями некоторого района. Найти вероятность того, что приобретенная электролампочка будет стандартной.

27. На фабрике изготовляющей болты, первая машина производит 25%, вторая - 35%, третья - 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2 %.Какова вероятность того, что выбранный болт дефектный?

28. В цехе работает 20 станков. Из них 10 - марки А, 6 - марки В, 4 - марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна: 0,9; 0,8; 0,7. Какой процент отличных деталей выпускает цех в целом?

29. В группе 10 юношей, которые играют, набрасывая кольца на колышек. Для пяти из них вероятность попадания кольца на колышек равна 0,6, для трех - 0,5, для остальных- 0,3. Какова вероятность того, что брошенное одним из юношей кольцо попало на колышек?

30. В ящик, содержащий три одинаковые детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.

 

Задача 13

1. В группе 10 юношей, которые играют, набрасывая кольца на колышек. Для пяти из них вероятность попадания кольца на колышек равна 0,6, для трех - 0,5 и для остальных - 0,3. Кольцо, брошенное одним из юношей, попало на колышек. Какова вероятность того, что это кольцо было брошено юношей из первой группы?

2. В одной студенческой группе обучаются 24 студента, во второй - 36 и в третьей - 40 студентов. По математическому анализу получили отличные оценки 6 студентов первой группы, 6 студентов второй группы и 4 студента третьей группы. Наугад выбранный студент получил по математическому анализу оценку “ отлично “. Какова вероятность того, что он учится в первой группе?

3. Преподаватель экзаменует незнакомую ему группу по экзаменационным билетам, содержащим по три вопроса. Он знает, что в предыдущую сессию в этой группе было 27 успевающих, из них 6 отличников, и трое в группе не успевало. Преподаватель считает, что отличники ответят на все три вопроса с вероятностью 80 %, остальные успевающие студенты - с вероятностью 60 % и неуспевающие с вероятностью 20 %. Вызванный студент ответил на все три вопроса билета. Какова вероятность того, что он из второй группы (успевающий, но не отличник)?

4. Для сдачи зачета студентам необходимо подготовить 30 вопросов. Из 25 студентов 10 человек подготовили ответ на все вопросы, 8 - на 25 вопросов, 5 - на 20 вопросов и двое - на 15. Вызванный наудачу студент ответил на поставленный ему вопрос. Найти вероятность того, что этот студент подготовил все вопросы.

5. Имеются три одинаковые урны. В первой находится 4 белых и 6 черных шаров, во второй - 7 белых и 3 черных и в третьей только черные. Шар, извлеченный наудачу из наудачу выбранной урны, оказался черным. Какова вероятность того, что шар извлечен из первой урны?

6. Имеется 10 одинаковых урн, из которых в 9 находятся по 2 черных шара и по 2 белых шара, а в одной - 5 белых и 1 черный шар. Из наугад взятой урны извлечен шар, оказавшийся белым. Чему равна вероятность, что он извлечен из урны содержащей 5 белых шаров?

7. Из урны, где находится 10 белых и 5 черных шаров, наугад перекладывают один шар во вторую урну, где находятся 3 белых и 6 черных шаров. После этого наугад из второй урны извлекают один шар, который оказался белым. Найти вероятность того, что из первой урны переложен белый шар.

8. Из трех команд - “Спартак”, “Динамо”, ”ЦСКА” - занимающих в турнирной таблице вторые места, каждая может попасть в финал с равной вероятностью и завоевать там первое место с вероятностями, соответственно равными 0,7; 0,6; 0,9. Найти вероятность того, что попала в финал и заняла первое место команда “ЦСКА”.

9. В рационе пеликанов, чаек и гагар, содержащихся в зоопарке, рыба занимает соответственно 70 %, 80 % и 90 %. Найти вероятность того, что в данное время служитель зоопарка кормит рыбой чайку, если в вольере содержится 10 пеликанов, 4 чайки и 8 гагар.

10. Из 20 девочек и 10 мальчиков, обучающихся в классе, не выполнили домашнего задания 4 девочки и 3 мальчика. Наудачу вызванный ученик не выполнил задание. Какова вероятность того, что вызван был мальчик?

11. Продукция первой фабрики составляет 20 % поступления, второй - 46 %, третьей - 34 %. Средний процент нестандартных изделий для первой, второй и третьей фабрик составляет соответственно 3, 2 и 1. Найти вероятность того, что взятое наугад изделие принадлежит первой фабрике, если оно оказалось нестандартным.

12. Две перфораторщицы набрали на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй эта вероятность равна 0,1. При сверке перфокарт обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица.

13. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму - 0,45. Вероятность того, что стандартное изделие будет стандартным первым товароведом, равна 0,9, а вторым - 0,98. Найти вероятность того, что изделие проверял второй товаровед.

14. Из 6 нападающих и 4 защитников в данный момент один человек находится на скамейке штрафников. Найти вероятность того, что это защитник, если вероятность попасть на скамейку штрафников для защитника равна 0,8 а для нападающего - 0,6.

15. Один из двух охотников стреляет по цели и попадает в нее. Вероятность попадания в цель для первого охотника равна 0,2, для второго - 0,6. Чему равна вероятность того, что стрелял первый охотник?

16. В оной урне 3 белых и 4 черных шара, а во второй 5 белых и 3 черных. Из первой и второй урн наудачу берут по одному шару и помещают в третью пустую урну. Найти вероятность того, что наугад извлеченный белый шар из третьей урны попал в нее из первой урны.

17. Вероятности попадания при каждом выстреле для трех стрелков соответственно равны 4/5,3/4, 2/3. При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.

18. Трое охотников одновременно выстрелили по вепрю, который был убит одной пулей. Определить вероятность того, что вепрь был убит третьим охотником, если вероятности попадания для них равны соответственно 0,2; 0,4; 0,6.

19. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 - с вероятностью 0,7; 4 - с вероятностью 0,6 и 2 - с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. Найти вероятность того, что он принадлежал ко второй группе.

20. Некто, заблудившийся в лесу, вышел на поляну, откуда вело 5 дорог. Известно, что вероятности выхода из леса за час для различных дорог равны соответственно 0,6; 0,3; 0,2; 0,1; 0,1. Чему равна вероятность того, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса через час.

21. На трех отделениях факультета повышения квалификации (ФПК) занимаются 100 человек. Из них к кафедрам математического анализа, методики преподавания математики, алгебры прикреплены соответственно 28, 40 и 32 человека. Вероятность того, что кто -то из слушателей ФПК будет назначен ответственным дежурным для прикрепленных к кафедрам математического анализа, методики преподавания математики и алгебры, различна и равна соответственно 0,2; 0,3; 0,4. Один из слушателей ФПК заступил на дежурство. Найти вероятность того, что он прикреплен к кафедре методики преподавания математики.

22. В скачках участвуют 7 лошадей кабардинской и 5 орловской породы. Вероятность того, что к финишу придет скакун кабардинской породы, равна 0,89, а для орловской породы эта вероятность равна 0,78. Найти вероятность того, что первым пересек линию финиша скакун кабардинской породы.

23. Пять студентов - любителей музыки, два юноши и три девушки - слушают концерт. Вероятность того, что очередному исполнителю одна из девушек преподнесет цветы, равна 0,5. Для юношей эта вероятность равна 0,3. Найти вероятность того, что букет цветов после очередного исполнения преподнес юноша. (Вместе цветы не преподносят).

24. Первый прибор регистрирует некоторое излучение с вероятностью 0,72. Если первый прибор не сработает, то включается второй, который зарегистрирует излучение с вероятностью 0,88. Найти вероятность того, что второй прибор зарегистрирует излучение.

25. В одной из урн 7 белых и 3 черных шара, а во второй - 4 белых и 5 черных. Из первой урны во вторую наудачу перекладывается один шар, а затем из второй урны извлечен один шар, который оказался белым. Найти вероятность того, что этот шар принадлежит первой урне.

26. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишень обнаружена одна пробоина. Найти вероятность того, что в мишень попал первый стрелок.

27. На фабрике, изготовляющей болты, первая машина производит 25 %, вторая 35 %, третья 40 % всех изделий. В их продукции брак составляет соответственно 5 %, 4% и 2 %. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной?

28. На первом заводе на каждые 100 лампочек приходится в среднем 10 нестандартных, на другом - 15, на третьем - 20. Продукция этих заводов составляет соответственно 50%, 30% и 20 % всех электролампочек, приобретаемых жителями некоторого района. Купленная лампочка оказалась стандартной. Найти вероятность того, что электролампочка изготовлена первым заводом.

29. Имеются две одинаковые урны. В первой - 7 белых шаров и 3 черных, во второй -6 белых и 4 черных. Наудачу выбирается урна и из нее наугад извлекается один шар. Шар оказался белым. Какова вероятность того, что шар извлечен из первой урны?

30. Плавучая станция получает в определенное время информацию от трех наземных станций с вероятностью 0,6; 0,75; 0,93. Найти вероятность того, что, пришедшая в данный момент информация передана третьей наземной станцией.