Решение нелинейных уравнений.
Цель работы: Изучение возможностей пакета Ms Excel 2007 при решении нелинейных уравнений и систем. Приобретение навыков решения нелинейных уравнений средствами пакета.
Найти корни полинома x3-0,01x2-0,7044x+0,139104=0.
Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль.
Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты вычислений приведены на рис. 1., где в ячейку В2была введена формула:
=A2^3-0,01*A2^2-0,7044*A2+0,139104.
Рис.1. Окно Excel
На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеется не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].
Теперь можно найти корни полинома методом последовательных приближений с помощью команды Сервис 
Подбор параметра (2007 данные - анализ если что - подбор параметра). Относительная погрешность вычислений и предельное число итераций (например, 0,00001 и 1000) задаются на вкладке Сервис Параметры. (устанавливаем курсор в ячейку в 14, выбираем данные - анализ если что - подбор параметров) и заполнить диалоговое окно следующим образом (см. рис. 2).
Рис.2. Подбор параметра
В поле Установить в ячейке дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения (уравнение должно быть записано так, чтобы его правая часть не содержала переменную). В поле Значение вводим правую часть уравнения, а в поле Изменяя значения ячейки дается ссылка на ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке.
После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (см. рис. 3) с сообщением об успешном завершении поиска решения, приближенное значение корня будет помещено в ячейку А14.
Рис.3. Результат подбора параметра
Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и А16 (см. рис. 4).
Рис.4. Получившиеся значения
ЗАДАНИЕ 1. Найти корни полинома.
| № | уравнение | № | уравнение |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
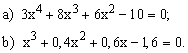
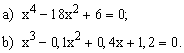
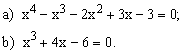
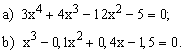
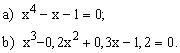
ЗАДАНИЕ 2. Найти решение нелинейного уравнения.
| № | уравнение | № | уравнение | № | уравнение |
| 
| 
| |||
|
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
|
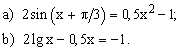
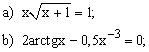
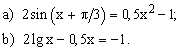
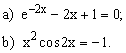
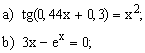
1.2.
Программа MS Excel имеет встроенные средства, с помощью которых можно без программирования решать нелинейные уравнения и осуществлять поиск максимального и минимального значений функции одной переменной в заданных границах.
Цель и содержание работы: овладеть практическими навыками решения нелинейных уравнений и поиска экстремумов функции одной переменной средствами программы MS Excel.
Решение нелинейных уравнений
В общем случае решение нелинейного уравнения проводится численно в два этапа (здесь речь идёт лишь о вещественных корнях уравнения). На первом этапе производится поиск интервалов, в которых содержится только по одному корню. Второй этап решения связан с уточнением корня в выбранном интервале (определением значения корня с заданной точностью). Известно, что корень уравнения (уравнение записано в виде f (x)=0) – это такое значение аргумента, при котором значение функции равно нулю. В графическом представлении – это может быть точка пересечения или касания графика функции с осью абсцисс.
При решении уравнения не надейтесь никогда найти точное значение корня и добиться обращения функции в нуль при использовании компьютера, где сами числа представлены ограниченным числом знаков. Здесь критерием может служить приемлемая абсолютная или относительная погрешность корня. Если, например, относительная погрешность равна 0,000001 (e =0,000001), то искомый результат буде иметь 6 верных (значащих) цифр после запятой (n = lg (1/ e)).
В настоящей лабораторной работе решение уравнений сводится к выполнению второго этапа, то есть к уточнению корня на заданном отрезке.
Решение нелинейных уравнений в таблицах MS Excel возможно осуществить следующими способами:
1) Подбором параметра;
2) используя циклические ссылки;
3) с помощью Поиска решения.
Подбор параметра
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность (относительная погрешность) устанавливаются следующей последовательностью команд:
1) щёлкнуть мышью по кнопке меню С е рвис;
2) в раскрывшемся меню щёлкнуть по строке П а раметры…;
3) в появившемся диалоговом окне Параметры щёлкнуть мышью по вкладке Вычисления, где и установить значения Предельного числа итераций и Относительной по г решности;
4) щёлкнуть по кнопке ОK.
При подборе параметра Excel изменяет значение аргумента функции в одной конкретной ячейке до тех пор, пока значения функции, вычисляемые по формуле, ссылающейся на эту ячейку, не станут соответствовать установленным параметрам вычислений.
Уточнение корня уравнения этим способом сводится к следующим действиям.
1) Заданное уравнение преобразовать к виду f (x)=0. Левая часть уравнения и будет той функцией, нуль которой необходимо найти. Например, задано уравнение tg (x)=1/ x. Приводим его к виду x × tg (x)=1, переносим единицу в левую часть уравнения и получаем x × tg (x)-1=0. Тогда функция, нуль которой предстоит найти, имеет вид f (x)= x × tg (x)-1.
2) В выбранную ячейку рабочего листа (например, B5) ввести текст x=.
3) В соседнюю справа ячейку (например, в ячейку C5) ввести любое начальное приближение к корню из заданного отрезка (можно использовать значение левой или правой границы).
4) В ячейку строкой ниже (например, B6) ввести текст f(x)=.
5) В соседнюю ячейку (справа от предыдущей) ввести выражение для вычисления значений функции, в качестве которой использовать левую часть уравнения (в нашем случае в ячейку C6 ввести формулу =C5*TAN(C5)-1). Ссылка в формуле вводится щелчком мыши по ячейке с начальным значением аргумента, то есть по ячейке C5.
6) Щёлкнуть мышью по ячейке с формулой для вычисления значений функции (C6).
7) Щёлкнуть мышью по строке меню С е рвис. (2007: данные – работа с данными – анализ если что – подбор параметра).
8) В раскрывшемся меню щёлкнуть по строке П одбор параметра….
9) В появившемся диалоговом окне Подбор параметра удалить адрес текущей ячейки в окне Установить в я чейке:, если он не соответствует адресу ячейки с выражением для вычисления значений функции, и щёлкнуть мышью по ячейке с формулой (C6), в окно Зна ч ение: ввести 0 (нуль). Щелкнуть мышью в окне И зменяя значение ячейки:, а затем щёлкнуть мышью по ячейке со значением x (C5).
10) Щёлкнуть мышкой по кнопке ОK. Результат получен.
Пример оформления на рабочем листе
| B | С | |
| x= | 0,5 | |
| f(x)= | =C5*TAN(C5)-1 |
Циклические ссылки
Если в ячейку рабочего листа введена формула, содержащая ссылку на эту же ячейку (может быть и не напрямую, а опосредованно – через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). Именно вычисление по формулам с циклическими ссылками и использовано в рассматриваемом способе решения нелинейных уравнений. При этом число повторений цикла будет конечным.
Для включения режима циклических вычислений надо выполнить следующие действия:
1) щёлкнуть мышью по кнопке меню С е рвис; (2007: Нажмите кнопку Microsoft Office 
, щелкните Параметры Excel, а затем выберите категорию Формулы.)
2) в раскрывшемся меню щёлкнуть мышью по строке П а раметры…;
3) в диалоговом окне Параметры щёлкнуть мышью по вкладке
Вычисления;
4) поставить флажок в окне и терации;
5) установить вариант вычислений автоматически;
6) щелкнуть мышью по кнопке ОK.
Уточнение корня уравнения этим способом сводится к следующим действиям.
1) Найти первую производную от функции f (x) из уравнения f (x)=0. В нашем примере производная от функции f (x)= x × tg (x)-1 будет иметь вид f /(x)= tg (x)+ x / cos 2(x).
2) В ячейку (например, F5) ввести текст Xнач=.
3) В ячейку ниже (F6) ввести текст x=.
4) В следующую ниже ячейку (F7) ввести текст f(x)=.
5) В ячейку G5 ввести начальное приближение x (число) к искомому корню. В качестве такого приближения можно использовать середину (левую или правую границу) заданного отрезка.
6) В ячейку G6 ввести рекуррентную формулу, задающую вычисление очередного приближения к корню по методу Ньютона 
. При этом необходимо использовать логическую функцию ЕСЛИ(). Применение этой функции позволит запустить итерационный процесс с начального приближения, записанного в G5. Таким образом, формула, которую надо ввести в ячейку G6, будет иметь вид: =ЕСЛИ(G6=0;G5;G6-(G6*TAN(G6)-1)/
(TAN(G6)+G6/COS(G6)^2)).
7) В ячейку G7 ввести выражение для вычисления значений функции из уравнения. Искомый результат (корень) будет получен в ячейке G6.
Для изменения начального приближения Xнач на другое необходимо выполнить следующие действия.
1) Из ячейки со значением Xнач (G5) удалить прежнее значение и ввести новое.
2) Дважды щёлкнуть мышью (перейти в режим редактирования содержимого) по ячейке с формулой (G6). После чего нажать клавишу Enter. Это приведёт к обнулению прежнего результата и повторному запуску итерационного процесса.
