Заметим, что любое расширение  поля
поля  можно рассматривать как линейное векторное пространство над полем
можно рассматривать как линейное векторное пространство над полем  , векторами которого являются все числа из поля
, векторами которого являются все числа из поля  (включая и числа поля
(включая и числа поля  ), а скалярами – числа из поля
), а скалярами – числа из поля  . Проверка для
. Проверка для  всех аксиом векторного пространства не вызывает затруднений.
всех аксиом векторного пространства не вызывает затруднений.
Для нас важен случай, когда пространство  конечномерно.
конечномерно.
Определение 1. Если расширение  поля
поля  является конечномерным пространством над полем
является конечномерным пространством над полем  , то
, то  называется конечным расширением поля
называется конечным расширением поля  , а его размерность (обозначаемая символом
, а его размерность (обозначаемая символом  ) – степенью конечного расширения поля
) – степенью конечного расширения поля  .
.
Теорема 1. Пусть в цепочке полей

каждое поле  является конечным расширением поля
является конечным расширением поля  степени
степени 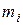 ,
,  . Тогда
. Тогда  является конечным расширением поля
является конечным расширением поля  степени
степени  .
.
Доказательству теоремы предпошлем лемму.
Лемма 1. Если система векторов
 (1)
(1)
есть базис пространства  над полем
над полем  , а система
, а система
 (2)
(2)
есть базис пространства 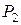 над полем
над полем  , то система
, то система
 (3)
(3)
является базисом пространства 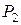 над полем
над полем  .
.
Доказательство. Требуется доказать, что система (3) линейно независима в пространстве 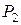 над полем
над полем  и каждый вектор из
и каждый вектор из 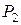 линейно выражается через систему (3).
линейно выражается через систему (3).
Пусть выполняется равенство
 ,
,  (4)
(4)
Переписывая это равенство в виде
 ,
,  ,
, 
и учитывая линейную независимость системы (2), заключаем:
 ,
, 
Но так как система (1) линейно независима в пространстве  над полем
над полем  , то из последних равенств вытекает:
, то из последних равенств вытекает:
 ,
,  ,
, 
Таким образом, равенство (4) возможно только при  , т.е. система (3) линейно независима в пространстве
, т.е. система (3) линейно независима в пространстве 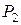 над полем
над полем  .
.
Пусть 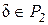 . Так как система (2) есть базис пространства
. Так как система (2) есть базис пространства 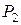 над полем
над полем  , то
, то
 ,
,  .
.
Но поскольку система (1) есть базис  над полем
над полем  , что
, что
 ,
, 
и, следовательно,

что и завершает доказательство леммы.
Из леммы 1 следует, что теорема 1 верна при  . Предположим, что теорема верна при
. Предположим, что теорема верна при  , т.е.
, т.е.  является конечным расширением поля
является конечным расширением поля  степени
степени  . Но так как
. Но так как  есть конечное расширение поля
есть конечное расширение поля  степени
степени  , то согласно лемме
, то согласно лемме  есть конечное расширение поля
есть конечное расширение поля  степени
степени  .
.
Таким образом, теорема верна при  , а, следовательно, и при любом натуральном значении
, а, следовательно, и при любом натуральном значении  .
.
Теорема 2. Если  – алгебраическое над полем
– алгебраическое над полем  число степени
число степени  , то система
, то система

 (5)
(5)
является базисом  над полем
над полем  .
.
Доказательство. Равенство

возможно только при  , Так как в противном случае степень числа
, Так как в противном случае степень числа  над полем
над полем  была бы меньше
была бы меньше  . Значит, система (5) линейно независима в пространстве
. Значит, система (5) линейно независима в пространстве  над полем
над полем  .
.
Пусть  . Тогда в силу теоремы 1 §2
. Тогда в силу теоремы 1 §2  ,
,  . Если
. Если 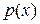 – минимальный многочлен числа
– минимальный многочлен числа  , то по теореме о делении с остатком
, то по теореме о делении с остатком

причем либо  , либо степень
, либо степень  меньше
меньше  . Значит,
. Значит,
 ,
,  ,
, 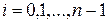
то есть  линейно выражается через векторы системы (5). Таким образом система (5) является базисом пространства
линейно выражается через векторы системы (5). Таким образом система (5) является базисом пространства  над полем
над полем  .
.
Следствие. Простое алгебраическое расширение  является конечным расширением поля
является конечным расширением поля  , причем степень этого расширения равна степени алгебраического над полем
, причем степень этого расширения равна степени алгебраического над полем  числа
числа  .
.
Теорема 3. Если поле  является конечным расширением поля
является конечным расширением поля  степени
степени  , то каждый элемент из поля
, то каждый элемент из поля  является алгебраическим над полем
является алгебраическим над полем  числом степени
числом степени  , где
, где  – некоторый делитель числа
– некоторый делитель числа  .
.
Доказательство. Так как  , то любая система, содержащая более
, то любая система, содержащая более  векторов, линейно зависима в пространстве
векторов, линейно зависима в пространстве  над полем
над полем  . В частности, если
. В частности, если 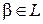 , то линейно зависима система
, то линейно зависима система

Это означает, что в поле  существуют такие числа
существуют такие числа  , из которых, по крайней мере, одно отлично от нуля, что
, из которых, по крайней мере, одно отлично от нуля, что

последнее равенство и означает, что число  алгебраично над полем
алгебраично над полем  .
.
Рассмотрим теперь цепочку полей.

Если система векторов из  линейно зависима над полем
линейно зависима над полем  , то она линейно зависима и над полем
, то она линейно зависима и над полем 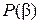 , и, следовательно,
, и, следовательно,  является конечным расширением поля
является конечным расширением поля 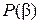 . Поэтому в силу теоремы 1
. Поэтому в силу теоремы 1

где число  есть в силу следствия из теоремы 1 степень алгебраического над полем
есть в силу следствия из теоремы 1 степень алгебраического над полем  числа
числа  .
.
Таким образом,  является делителем числа
является делителем числа  , что и завершает доказательство теоремы.
, что и завершает доказательство теоремы.
Следствие. Все элементы простого алгебраического расширения поля  алгебраичны над полем
алгебраичны над полем  .
.
Составные расширения
Пусть  – множество чисел, не обязательно алгебраических над полем
– множество чисел, не обязательно алгебраических над полем  . Присоединим к полю
. Присоединим к полю  число
число  , затем к полю
, затем к полю  – число
– число  и т.д. В результате получим цепочку полей
и т.д. В результате получим цепочку полей
 ,
,
в которой каждое поле, начиная с  , является простым расширением соседнего предшествующего поля. Тогда поле
, является простым расширением соседнего предшествующего поля. Тогда поле  при
при 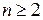 , называется составным расширением поля
, называется составным расширением поля  .
.
Заметим, что два соседних поля  и
и  могут и совпадать; это возможно тогда и только тогда, когда
могут и совпадать; это возможно тогда и только тогда, когда  .
.
Теорема 1. Составное расширение  является минимальным расширением поля
является минимальным расширением поля  , содержащим множество
, содержащим множество 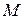 . Иначе говоря,
. Иначе говоря,  является пересечением всех числовых полей, содержащих поле
является пересечением всех числовых полей, содержащих поле  и множество
и множество 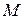 .
.
□ Обозначим через 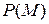 пересечение всех числовых полей, содержащих подполе
пересечение всех числовых полей, содержащих подполе  и множество
и множество 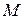 . Требуется доказать, что
. Требуется доказать, что  . Включение
. Включение  очевидно. С другой стороны, так как
очевидно. С другой стороны, так как  и
и  , то в силу минимальности простого расширения поля
, то в силу минимальности простого расширения поля  справедливо включение
справедливо включение  . Аналогично, так как
. Аналогично, так как  и
и  , то в силу минимальности простого расширения
, то в силу минимальности простого расширения  поля
поля  справедливо включение
справедливо включение  . Индукцией по
. Индукцией по  легко доказывается и включение
легко доказывается и включение  . Учитывая ранее отмеченное включение
. Учитывая ранее отмеченное включение  , получим требуемое равенство
, получим требуемое равенство  . ◘
. ◘
Следствие. Составное расширение  не зависит от порядка присоединения элементов
не зависит от порядка присоединения элементов  . ◘
. ◘
В дальнейшем, когда порядок присоединения элементов  не имеет значения, мы будем обозначать составное расширение
не имеет значения, мы будем обозначать составное расширение  через
через  или через
или через 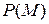 .
.
Следующая теорема дает информацию о внутреннем строении составного расширения.
Теорема 2 (о строении составного расширения). Составное расширение  есть множество чисел представимых в виде частного значений многочленов от
есть множество чисел представимых в виде частного значений многочленов от  переменных с коэффициентами из поля P от чисел
переменных с коэффициентами из поля P от чисел  , т.е.
, т.е.
 . (1)
. (1)
Обозначим через 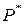 правую часть равенства (1). Это множество замкнуто относительно вычитания и деления на неравные нулю числа и, следовательно, является подполем поля
правую часть равенства (1). Это множество замкнуто относительно вычитания и деления на неравные нулю числа и, следовательно, является подполем поля  . Нетрудно проверить, подбирая соответствующим образом многочлены
. Нетрудно проверить, подбирая соответствующим образом многочлены 
 и
и 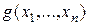 , что
, что  и
и  . Но тогда в силу теоремы 1 справедливо включение
. Но тогда в силу теоремы 1 справедливо включение  .
.
С другой стороны, очевидно, что все числа из 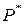 принадлежат полю
принадлежат полю  , и, следовательно,
, и, следовательно,  . Следовательно,
. Следовательно, 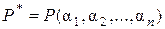 , что и требовалось доказать. ◘
, что и требовалось доказать. ◘






