На основеобобщения и синтеза классической механики Галилея – Ньютона и электродинамики Максвелла – Лоренца А. Эйнштейн создалв 1905 г. специальную теорию относительности. Она описывает законы всех физических процессов при скоростях движения, близких к скорости света, но без учета поля тяготения.
А. Эйнштейн сформулировал обобщенный принцип относительности, который теперь распространяется и на электромагнитные явления, в том числе и на движение света: никакими физическими опытами (механическими, электромагнитными и др.), производимыми внутри данной системы отсчета, нельзя установить различие между состояниями покоя и равномерного прямолинейного движения.
Эйнштейн показал, что для всех физических процессов скорость света обладает свойством бесконечной скорости. Для того чтобы сообщить телу скорость, равную скорости света, требуется бесконечное количество энергии. В измерениях, которые проводились над электронами, выяснилось, что кинетическая энергия точечной массы растет быстрее, нежели квадрат ее скорости, и становится бесконечной для скорости, равной скорости света.
Скорость света является предельной скоростью распространения материальных воздействий. Она не может складываться ни с какой скоростью и для всех инерциальных систем оказывается постоянной.
Из двух принципов: а) постоянства скорости света и б) расширенного принципа относительности Галилея – математически следуют все положения специальной теории относительности (СТО).
Физические величины длины тела, промежутка времени, массы для разных систем отсчета будут различными. Так, длина тела в движущейся системе будет наименьшей по отношению к покоящейся. По формуле:

где l΄ — длина тела в движущейся системе со скоростью V по отношению к неподвижной системе;
l — длина тела в покоящейся системе.
Время же будет как бы растягиваться, течь медленнее в движущейся системе по отношению к неподвижной, в которой этот процесс будет более быстрым. По формуле:
 ,
,
где t - промежуток времени в покоящейся системе,
t΄ - промежуток времени в движущейся системе.
Эффекты специальной теории относительности обнаруживаются при скоростях, близких к световым. При скоростях, значительно меньших скорости света, формулы СТО переходят в формулы классической механики.
Эйнштейн попытался наглядно показать, как происходит замедление течения времени в движущейся системе по отношению к неподвижной. Представим себе железнодорожную платформу, мимо которой проходит поезд со скоростью, близкой к скорости света (см. рис. 1).
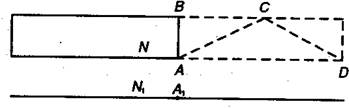
Рис. 1. К определению эффектов СТО.
В точке А1на платформе находится наблюдатель N1.На полу вагона в точке Аразмещен фонарик. Когда происходит совмещение точки А в вагоне с точкой А1на платформе, фонарик включается, появляется луч света. Так как скорость его конечная, хотя и большая, то для того чтобы достигнуть потолка вагона, где расположено зеркало, и отразиться обратно, необходимо время, за которое поезд уйдет вперед.
Для наблюдателя в вагоне луч света пройдет путь 2АБ, а для наблюдателя на платформе — 2АС. Как видно из рисунка, чем больше скорость поезда, тем длиннее линия АС. Очевидно, что 2АС > 2АВ. Этокак раз и говорит о замедлении течения времени внутри движущейся системы по отношению к неподвижной.
Релятивистское замедление времени является экспериментальным фактом. В космических лучах в верхних слоях атмосферы образуются частицы, называемые пи-мезонами, их собственное время жизни — 10-8 с. За это время, двигаясь даже со скоростью, почти равной скорости света, они могут пройти не больше чем 300 см. Но приборы их регистрируют. Они проходят путь, равный 30 км, или в 10 000 раз больше, чем для них возможно. Теория относительности так объясняет этот факт: 10-8 с является естественным временем жизни мезона, измеренным по часам, движущимся вместе с мезоном, т.е. покоящимся по отношению к нему. Но в системе отсчета Земли время жизни мезона намного больше, и за это время пионы в состоянии пройти земную атмосферу.
В общей теория относительности (ОТО), или теории тяготения, Эйнштейн расширяет принцип относительности, распространяя его на неинерциальные системы. В ней он также исходит из экспериментального факта эквивалентности масс инерционных и гравитационных, или эквивалентности инерционных и гравитационных полей.
Правда, принцип эквивалентности справедлив только при строго локальных наблюдениях. Так, представим себе лифт, стоящий на Земле. Наблюдатель в лифте бросает два шара. Они будут двигаться по направлению к центру Земли и, следовательно, друг к другу. Если же мы будем тянуть лифт с ускорением g в пустоте, то те же шары будут двигаться параллельно друг другу (см. рис. 2).

Рис.2. К эквивалентности инерционных и гравитационных масс.
Но, несмотря на это ограничение, принцип эквивалентности играет важную роль в науке. Мы всегда можем вычислить непосредственно действие сил инерции на любую физическую систему, и это дает нам возможность знать действие поля тяготения, отвлекаясь от его неоднородности, которая часто очень незначительна.
Эйнштейн предлагает провести мысленный эксперимент с лифтом, подвешенным над Землей. Представим себе, что в какой-то момент времени канат, на котором подвешен лифт, обрывается, и наблюдатели в нем оказываются в состоянии свободного падения. В этом случае они не смогут определить, какое из двух противоположных утверждений будет истинным: 1) лифт движется в поле тяготения Земли; 2) лифт покоится в отсутствие поля тяготения.
Если же в отсутствие поля тяготения Земли лифт будут тянуть вверх с ускорением g, то наблюдатели также не смогут выбрать истинное утверждение из двух противоположных: 1) лифт покоится в поле тяготения Земли; 2) лифт движется с ускорением в отсутствие поля тяготения.






