Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні відповідно даним мимобіжним прямим.
Кут між мимобіжними прямими, як і між прямими однієї площини, не може бути більше 90°. Дві мимобіжні прямі, які утворюють кут в 90°, називаються перпендикулярними.
Розв'язування вправ
1. Покажіть перпендикулярні мимобіжні прямі в оточенні.
2. Дано зображення куба (рис. 275). Знайдіть кут між мимобіжними прямими а і b.
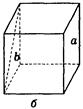
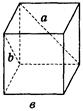
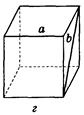
Рис. 275
(Відповідь, а) 90°; б) 45°; в) 60°; г) 90°; д) 90°; е) 90°.)
3. Дано куб ABCDA1B1C1D1. Доведіть, що АВ1 
CD1.
4. Пряма SA перпендикулярна до сторін АВ і АС трикутника АВС. Знайти кут між прямими SA і ВС. (Відповідь. 90°.)
5. Точки К і М середини ребер АВ і DC трикутної піраміди DABC, кожне ребро якої дорівнює а. Доведіть, що KM АВ. Знайдіть довжину відрізка KM.
(Відповідь. 
.)
6. Знайдіть кут між мимобіжними діагоналлю грані куба і діагоналлю куба.
Розв'язання
Знайдемо кут між діагоналлю ВD1 куба і діагоналлю DC1 грані куба (рис. 276). Добудуємо до даного куба куб ADMNA1D1M1N1 (рис. 277), тоді кут між прямими BD1 і DC1 дорівнює куту між прямими BD1 і D1M. Нехай АВ = а; тоді D1M = 
а, AD1 = 
a, ВМ = 
а.
Із ΔBD1M маємо:
ВМ2 = DB2 + D1M2 – 2AD1 · D1M cosBD1M, або
5 а 2 = 2 а 2 + 3 а 2 – 2 а · a cos BD1M;
5 а 2 = 5 а 2 – 2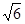 
а 2 cos <BD1M;
2 а 2 cos <BD1M = 0;
cos <BD1M = 0;
<BD1M = arccos 0 = 90°.
Відповідь. 90°.
7. Довести, що кут між мимобіжними прямими не залежить від вибору прямих, що перетинаються
Кут між прямою і площиною
Кут між прямою і площиною. Що розуміють під кутом між прямою і площиною? 
Якщо пряма паралельна площині, то вважають, що кут між такою прямою і площиною дорівнює 0°. Якщо пряма перпендикулярна до площини, то кут між ними дорівнює 90. У решти випадків кутом між прямою і площиною називають кут між прямою і її ортогональною проекцією на площину.
Приклад. Нехай АВСDА1В1С1D1 - куб (мал. 235). Знайдіть кут між прямою АС1 і площиною його грані АВСD. Проекція відрізка АС1 на площину грані АВСD - відрізок АС. Тому шуканий кут. Його тангенс, звідси.
До кута між прямою і площиною близьке поняття кута між похилою і площиною.
Кутом між похилою і площиною називають кут між похилою і її проекцією на площину.
Йдеться про прямокутну (ортогональну) проекцію. Якщо – кут між прямою і площиною, то 0° < < 90°; якщо – кут між похилою і площиною, то 0° < < 90°.
Можна довести, що кут між похилою і площиною найменший з усіх кутів, які похила утворює з прямими, проведеними на площині через основу похилої.
Кути між прямими і площинами часто доводиться вимірювати астрономам, геодезистам, географам, маркшейдерам, працівникам транспорту. Найпростіший саморобний прилад для вимірювання кутів між горизонтальною площиною і похилими – екліметр (мал. 236). Бувають екліметри і фабричного виготовлення (мал. 237). У його циліндричному корпусі при натиснутій кнопці вільно обертається і встановлюється за виском градуйований диск.
Якщо кнопку відпустити, диск закріплюється, і на його шкалі можна прочитати градусну міру кута, який вимірюють. Якщо потрібна більша точність, кути вимірюють теодолітами (мал.238).
Теодоліт має два круги з градусними поділками (лімби). Користуючись горизонтальним лімбом, визначають кути в горизонтальній площині, вертикальний лімб дає змогу вимірювати кут між горизонтальною площиною і похилими до неї напрямами.
Кут між площинами. Якщо дві площини паралельні, то вважається, що кут між ними дорівнює 0°. Якщо площини α і β перетинаються по прямій с, то, щоб визначити кут між цими площинами, у кожній з них через довільну точку М прямої с можна провести прямі а і b, перпендикулярні до прямої с. Кут між прямими а і b, приймають за кут між даними площинами α і β. Можна довести, що міра цього кута не залежить від вибору точки О на прямій с. Кут між двома площинами, як і між двома прямими, знаходиться в межах від 0° до 90°.
Якщо кут між двома площинами дорівнює 90°, то площини перпендикулярні.
Якщо дві площини перетинаються, то вони весь простір поділяють на 4 частини, які називають двогранними кутами.
Двогранним кутом називається частина простору, обмежена двома півплощинами, які виходять з однієї прямої.
Півплощини, які обмежують двогранний кут, називають його гранями, а їх спільну пряму – ребром двогранного кута (мал. 239).
Кут, утворений перетином двогранного кута з площиною, перпендикулярною до його ребра, називають лінійним кутом даного двогранного кута. Будь-які два лінійні кути двогранного кута рівні (мал. 240).
Тому двогранні кути можна характеризувати відповідними лінійними кутами.
Якщо, наприклад, лінійний кут деякого двогранного кута дорівнює 60°, то кажуть, що це – двогранний кут 60°. Двогранний кут називають гострим, прямим, тупим, розгорнутим чи більшим від розгорнутого залежно від того, чи є його лінійний кут гострим, прямим, тупим, розгорнутим чи більшим від розгорнутого (мал. 241).
Не слід ототожнювати міру двогранного кута з кутом між площинами. Кут між площинами може змінюватися в межах від 0° до 90°, а міра двогранного кута - від 0° до 360°.
Замість «двогранний кут, міра якого дорівнює α» нерідко кажуть коротше: «двогранний кут α». У таких випадках під двогранним кутом розуміють і певну фігуру, і відповідне її числове значення. 
Найпростішими матеріальними моделями двогранного кута є краї різальних інструментів: зубил, стамесок, різців для токарних верстатів тощо. Вони бувають більш або менш гострими. Вимірюють такі кути кутомірами (мал. 242).
Закріплення нового матеріалу (10 хв.) (для виконання завдань учні об’єднуються у групи)
Розв’язати задачу.
Усно
ІІ варіант. І варіант
Знайти кут між прямими
а) АВ і АД1 а) АВ1 і АД1
б) АВ1 і АД б) ДС1 і А1Д1
в) АВ1 і АВ в)CД1 і СВ1
Відповідь: а)90˚ б)60˚ в)45˚ а)60˚ б)90˚ в)45˚
2) Дано зображення куба знайдіть кут між мимобічними прямими.
а)90 в)60 б)45 г)90
3) Дано зображення куба. Знайти кут між площиною АВС і прямою.
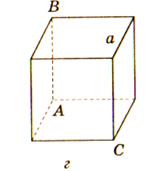
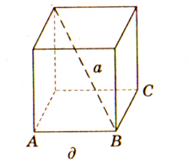
Відповідь: г)45 б)0; а)90 д) аrtg 1⁄√2
Знайдіть кут між площинами АВС і АВD
Відповідь:
а) 90º в) arctg √2 б) 45º г)arctg √2
2 2
Письмове розв’язування задач
Користуючись зображенням, знайдіть: SA і SB – похилі
SO =a, ےАОВ=90°
І ІІ
1. Проекцію похилої SA на площину АОВ;
2. довжину похилої SA;
3. проекцію похилої SB на площину АОВ;
4. довжину похилої SB;
5. відстань між основами похилих;
6. відстань між прямими SO і АВ.
І в. 1) а; 2) 2а; 3) а; 4) а√2; 5) 2а√3; 6) а
√3 √3 3 2
ІІ в. 1) а; 2) а√2; 3) а√3; 4) 2а; 5) 2а; 6) а√3
2.
Самостійне розв’язування задач із подальшим записом на дошці.
1.Точка А віддалена від площини 
на 2 м. Знайдіть довжину похилої АВ, нахиленої до під кутом 30˚.
2. знайдіть довжину проекції похилої та відстань від точки А до площиин α, якщо похила дорівнює 10 см. і утворює із площиною кут 30º
3. Знайди довжину похилої та її проекції, якщо точка А віддалена від площиини α на 6 см., а похила утворює з площиною кут -30º.
Домашнє завдання
Бевз Г.П. Математика: 10 кл. § 33, № 1190, 1195.
Література
1.Державний стандарт базової і повної середньої освіти //Постанова КМУ № 1392 від 23 листопада 2011 р.
2.Робоча навчальна програма з математики для підготовки кваліфікованих робітників будівельного профілю. Рівень стандарт, - Калуш, 2015.
3. Бевз Г.П. Математика: 10 кл.: підруч. для загальноосвт. навч. закл.: рівень стандарту. – К.: Генеза, 2011, - 272 с.
4. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Математика. 10 клас. Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. – Тернопіль: Навчальна книга – Богдан. 2010. – 480 с.
Висновки
В процесі уроку всі завдання вчителя виконані на високому рівні. В процесі уроку виконані освітні, виховні і розвиваючі завдання.
