Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) с двумя неизвестными графическим методом с использованием табличного процессора Microsoft Excel.
Порядок выполнения работы
1. Выяснить у преподавателя номер своего варианта и в соответствии с этим номером получить индивидуальное задание на лабораторную работу.
2. Для задачи ЛП, описанной в индивидуальном задании, найти оптимальное решение графическим методом, используя для этого возможности табличного процессора Microsoft Excel.
3. Составить отчет о проделанной работе (распечатать результаты), продемонстрировать его преподавателю и защитить работу, отвечая на вопросы по изученной теме.
Инструкции по использованию Microsoft Excel для решения задачи ЛП от двух переменных графическим методом.
Рассмотрим процесс выполнения лабораторной работы в среде Excel на конкретном примере.
Допустим, для некоторой задачи была построена следующая математическая модель. Требуется найти максимум функции F(x1,x2)= 3x1-2x2 при следующих ограничениях: 2x1+2x2£10
-x1+3x2£5
2x1+x2³1
x1³0; x2³0
Для решения задачи необходимо выполнить следующую последовательность действий:
1. Запустить Microsoft Excel, в результате чего по умолчанию будет создан новый документ.
2. На текущей странице сделать заглавие документа, которое в обязательном порядке должно включать ФИО и группу студента, а также постановку задачи (рис.1).

3. Сформировать столбец исходных значений для переменной х1 в диапазоне от 0 до, например, 10 с шагом 0,5. Если потом окажется, что такого диапазона исходных данных не хватает для изображения всей области допустимых решений (ОДР), то диапазон нужно будет расширить.
Для начала следует ввести в пустую ячейку имя столбца – X1. Допустим, что адрес этой ячейки A11. Далее в следующую ячейку столбца (A12) вводим начальное значение, равное нулю. В ячейку A13 помещаем формулу =A12+0,5. Выделяем ячейку A13 и копируем ее в буфер. Выделяем группу ячеек A14-A32 и вставляем в эту группу формулу из буфера. Таким образом, у нас получился столбец исходных данных, в каждой ячейке которого (кроме первой), находится значение, вычисленное по формуле Z+0,5, где Z – адрес предыдущей ячейки столбца (рис.2). 
4. Рассматривая ограничения как равенства, выразить х2 через х1 и сформировать для каждого уравнения столбец значений х2, вычисляемых по соответствующим значениям х1. Считая целевую функцию равной нулю, проделать аналогичную операцию также и для нее.
Столбцы со значениями должны располагаться рядом друг с другом и образовывать матрицу. Каждый столбец должен иметь имя. В данном случае именами являются уравнения: x2=(10-2x1)/2; x2 = (5+x1)/3;
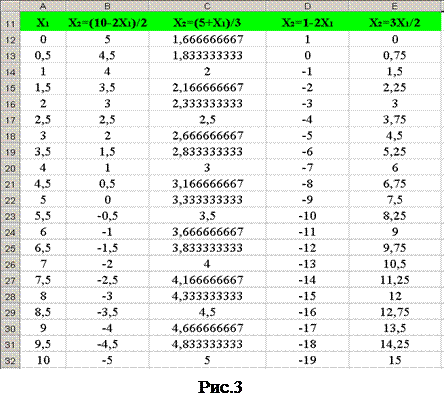
x2 = 1 – 2x1; x2=3x1/2. Далее в следующей ячейке столбца, т.е. под его именем, записываем формулу для вычисления значения x2 от первого значения x1. Например, для второго столбца в ячейке B12 будем иметь формулу =(10-2*A12)/2. После чего содержимое ячейки B12 следует скопировать в буфер и, выделив последующие ячейки B13-B32, вставить в них содержимое буфера. Аналогичные манипуляции следует выполнить для вычисления значений x2 от x1 для всех оставшихся выражений. В результате у вас должна получиться матрица, похожая на изображенную на рисунке 3.
 |
5. Построить графики по имеющимся данным.
Для этого следует выделить всю матрицу, включая имена столбцов, кроме первого столбца, и запустить мастера построения диаграмм. В рассматриваемом примере выделенными будут ячейки B11-E32. На закладке «Нестандартные» следует выбрать тип диаграммы «Гладкие графики» и нажать кнопку «Далее». На втором шаге построения диаграммы необходимо указать источник данных по оси абсцисс. По умолчанию это ряд чисел 1,2,3,…, который необходимо сменить на ряд, записанный в столбце Х1. Для этого выбираем закладку «Ряд» и в поле «Подписи по оси Х» задаем диапазон адресов ячеек, в которых хранится интересующий нас ряд. Задать диапазон удобней всего при помощи специального инструмента выбора Excel, вызвать который можно нажатием кнопки, расположенной в правой части поля ввода (рис.4.).

|
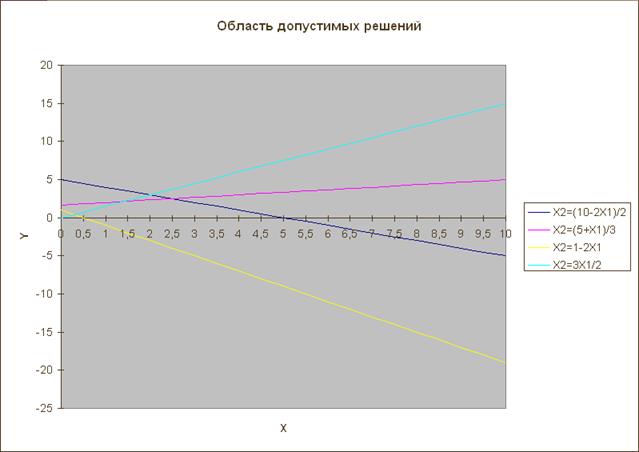
В результате нажатия на показанную кнопку диалог свернется до одного поля ввода, чтобы не мешать процессу выбора, и указатель мыши сменится на крестик. Далее необходимо выбрать ячейки, содержащие значения Х1 (в нашем примере это ячейки A12-A32), за исключением ячейки с именем столбца. Адреса выбранных ячеек с учетом рабочего листа появятся в поле ввода свернувшегося диалога. Далее диалог следует развернуть, нажав кнопку, справа от поля ввода и перейти к третьему шагу построения диаграммы, нажав кнопку «Далее». На третьем шаге в закладке «Заголовки» следует ввести название диаграммы - «Область допустимых решений», названия оси Х – «Х1», название оси Y – «Х2». В других закладках диалога третьего этапа лучше ничего не менять и нажать кнопку «Далее». На четвертом шаге требуется просто подтвердить расположение создаваемой диаграммы на текущем листе, нажав кнопку «Готово».
Появившуюся диаграмму расположите под таблицей исходных данных и увеличьте в размерах в два раза (рис.5).
|
|
|
6. Рассмотреть получившуюся диаграмму и определить, существует ли область допустимых решений (ОДР). Напоминаем, что ОДР должна быть выпуклой, и может представлять собой точку, отрезок, выпуклый многоугольник, полуплоскость. ОДР также может и не существовать, если ограничения несовместны. В ОДР может не существовать оптимального решения, если она не ограничена в направлении поиска оптимума. В случае несовместности ограничений или неограниченности ОДР в нужном направлении следует обратиться к преподавателю, доказать полученные выводы, внести предложения по изменению условий задачи так, чтобы оптимальное решение существовало и решить задачу при новых условиях.
Чтобы определить форму ОДР надо рассмотреть каждую из построенных прямых по отдельности и, заменив мысленно в соответствующем уравнении знак равенства на исходное неравенство, определить, с какой стороны от рассматриваемой прямой лежит ОДР. Для этого необходимо решить соответствующее неравенство относительно точки (0,0). Если неравенство истинно, то ОДР лежит в полуплоскости, которой принадлежит точка (0,0), если ложно – то в полуплоскости, которая не содержит точку (0,0).
ОДР будет являться областью пересечения всех полуплоскостей, задаваемых неравенствами-ограничителями.
7. Определив на диаграмме область расположения ОДР, диаграмму нужно отмасштабировать таким образом, чтобы ОДР была четко видна.
Масштабирование состоит из двух этапов: изменения масштаба оси абсцисс и изменения масштаба оси ординат.
Дважды щелкните левой кнопкой мыши на оси значений (ось ординат). В появившемся диалоге «Формат оси» выберите закладку «Шкала» и установите максимальное и минимальное значение шкалы так, чтобы получившийся диапазон был немного больше протяженности ОДР по этой оси. Также может потребоваться изменить цену основных и промежуточных делений.
В рассматриваемом примере минимальное значение по оси значений было установлено равным -5, максимальное 5, цена основных делений 1, цена промежуточных делений 0,5.
Изменение формата оси абсцисс производится путем сокращения рядов данных, по которым строятся графики. Для этого необходимо вызвать диалог «Исходные данные» из всплывающего меню диаграммы и уменьшить (при необходимости) на некоторое число адрес последней ячейки с данными, а также увеличить (при необходимости) адрес начальной ячейки с данными. Указанную операцию по изменению адресов начальных и конечных ячеек с данными надо проделать для всех рядов, изображаемых на данной диаграмме, а также для разметки оси абсцисс (иначе увеличения масштаба изображения, не растягивая диаграмму до огромных размеров, достичь не удастся).
В рассматриваемом примере крайняя правая точка ОДР имеет координаты (5,0), а это значит, что часть диаграммы расположенную правее этой точки можно не рассматривать. Отсечем диаграмму справа, начиная с точки (6,0). Для этого определим адрес ячейки столбца данных Х1, в которой лежит число 6. Это ячейка A24 (см. рис.1), значит 24-я строка должна ограничивать ряд исходных данных для всех графиков. Вызываем диалог «Исходные данные» и в закладке «Ряд» изменяем адреса последних ячеек для всех рядов с $B$32, $C$32, $D$32, $E$32 соответственно на $B$24, $C$24, $D$24, $E$24. Также изменяем адрес последней ячейки в поле «Подписи по оси Х» с $A$32 на $A$24 (см. рис. 6)
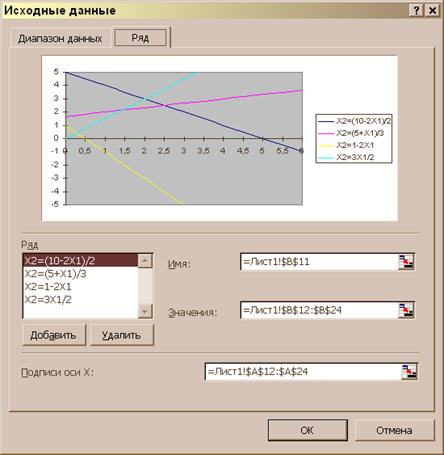
Рис. 6.
Нажимаем ОК. После масштабирования диаграмма выглядит как показано на рисунке 7.
Примечание: масштабирование следует проводить так, чтобы фрагменты всех прямых, включая прямую целевой функции, были видны.
|
|
|
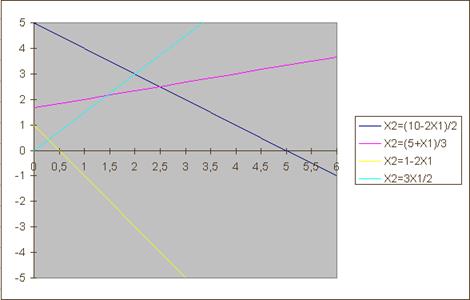
Рис. 7.
8. На построенной диаграмме выделить ОДР жирными линиями или обвести полилинией, для чего воспользоваться соответствующим инструментом Excel для рисования.
|

|
|
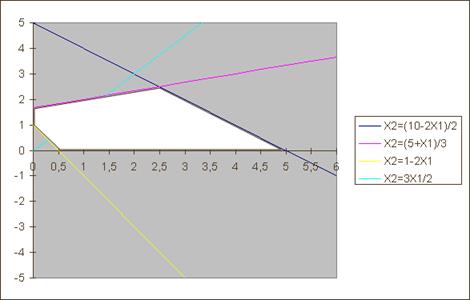
Рис. 8.
9. Найти на графике прямую целевой функции. На рис.8 фрагмент этой прямой обозначен отрезком AB. Найти градиент целевой функции в точке (0,0) и обозначить его направление стрелкой. В данном случае градиент имеет координаты {(0,0), (3,-2)}. Поскольку требуется найти максимум целевой функции, то начинаем мысленно сдвигать прямую целевой функции в направлении градиента (в случае поиска минимума сдвигать следует в направлении антиградиента), и определяем, что последняя точка ОДР, которая лежит на пути прямой, имеет координаты (5,0) (выделяем точку на графике), а максимум функции равен 15 (подставляем координаты точки в целевую функцию).
10. В случае, если точку оптимума по графику точно определить нельзя, то ее координаты следует находить путем решения уравнения, составленного из уравнений 2-х прямых, пересекающихся в ней.
Для решения уравнения также можно воспользоваться возможностями Excel. Например, найдем точку пересечения прямых X2=3X1/2 и X2=1-2X1. Для этого приравняем правые части этих уравнений 3X1/2 = 1-2X1 и преобразуем данное уравнение так, чтобы оно было равным, например, нулю: 3X1/2 + 2X1 – 1=0. Далее в какой либо свободной ячейке (допустим это B50) записываем формулу: =3*A50/2 + 2*A50 – 1. Здесь ячейка А50 нужна нам для хранения значения искомой переменной X1. Предположим, что эта переменная равна 0 и занесем 0 в ячейку А50.
Для решения уравнений, а также для аналитического решения задач ЛП, в Excel используется компонент «Поиск решения». Данный компонент вызывается из меню «Сервис» и может быть недоступен по умолчанию. Если так, то его необходимо подключить, выбрав пункт «Надстройки» из меню «Сервис». В появившемся диалоге необходимо поставить галочку напротив компонента «Поиск решения» и нажать «ОК».
Вызываем компонент «Поиск решения» и в появившемся диалоге в качестве целевой ячейки устанавливаем ячейку, содержащую решаемое уравнение (в нашем примере это $B$50), а ячейку $A$50 устанавливаем в качестве изменяемой. ($ обозначает абсолютную адресацию ячеек) В разделе «Параметры» рассматриваемого диалога выбираем тип модели «Линейная модель», нажимаем «ОК» и «Выполнить». Excel решит заданное уравнение с определенной точностью и сформирует решение в ячейке А50. В нашем случае Х1 искомой точки равен 0,285714285714227. Чтобы узнать теперь чему равна координата X2 точки пересечения просто корректируем формулу в ячейке B50, приводя ее к виду одного из уравнений пересекающихся прямых. В нашем случае получаем, что искомая точка имеет точные координаты (0,285714285714227; 0,428571429)
11. Выполненную лабораторную работу следует сохранить на рабочем диске, в папке с именем своей группы, в индивидуальном каталоге.
12. Распечатанный отчет о выполнении лабораторной работы должен содержать:
- титульный лист;
- постановку задачи;
- расчетную таблицу (рис. 3);
- график с выделенной ОДР, искомой точкой оптимума и направлением градиента;
- расчет координат точки оптимума и значения целевой функции в этой точке.






