Зертханалық жұмыс №2
Фурье түрлендірулері. Сигналдарды спектрлік талдау.
Жұмыс мақсаты.
Фурье түрлендіруін менгеру. Сигналдардың АЖС және ФЖС алып үйрену. Сигналдардың спектрлерін табу үшін MATLAB ортасында Фурье түрлендірулерін қолдану дағдысын қалыптастыру.
ысқаша теориялық кіріспе
Фурье қатары - [а,b] кесіндісінде ортонормаланған φ1(х), φ2(х),...,φn(х),... функциялар жүйесі бойынша f(x) функциясының Фурье қатары деп 
қатарын айтады. Мұндағы сk Фурье коэффициенттері:
1, cosnx, sinnx, n=1,2,..., тригонометриялық жүйесіндегі Фурье қатары:
мұндағы a0, ak, bk - Фурье коэффициенттері.
Фурье түрлендіру - f(x) функциясының фурье түрлендіру деп f(x)-пен төмендегі формула арқылы байланысатын F(z) функциясын айтады: 
Осымен қатар Фурье формуласы:
аралығындағы барлық (мүмкін, саны ақырлы нүктелерінен басқа) х нүктелерінде орындалады деп есептеледі.
Сигналдың уақыттық көрінісі ретінде s (t) уақыт функциясы алынады.Сигналдың жиіліктік көрінісі ретінде S (f) жиілікті функция қолданылады. s (t) және S (f) функциялары Фурье турлендірулері арқылы байланысқан.
(1)
Бірінші қатар тура Фурье турлендіруі,ал екіншісі кері Фурье турлендіруі деп аталады. S (f) функциясы s (t)функцясының спектрлік функциясы деп аталады.
S (f)функциясы комплексті функция және ол алгебралық және көрсетілген формада қарастырылған.
S (f) спектрімен АЖС A (f) және ФЖС j (f) сигналдарын мына байланыс арқылы алуға болады.
(2)
Фурье турлендіруінің құрылысынан мынаны атап өтуге болады. Біріншіден, егер 
сигнал заттық функция болса, S (f) спектрі үшін жұптылық байланыстың мына түрі орындалады.
Бұл байланыстан заттық сигнал үшін АЖС –жұп функция, ал ФЖС– тақ функция.
Екіншіден, сигнал уақыттың заттық жұп функциясы
,
болса, спектр үшін мына байланыс орындалады
Бұл жерде спектрдің жалған бөлігі нөлге тең
Үшіншіден егер сигнал уақыттық заттың тақ функциясы болса,
,
онда спектр үшін мына байланыс орындалады
Бұл жерде спектрдің шын бөлігі нөлге тең
Бірінші мысал ретінде t ұзақтылыққа және уақыттың бастапқы есебіне байланысты центрленген тікбұрышты импульсті қарастырамыз.
Тура Фурье түрлендіруі арқылы S (w) спектрін есептейміз
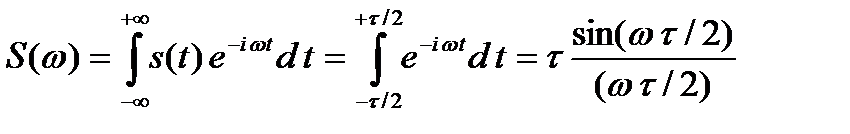
Циклдік жиілік w = 2 p f. АЖС және ФЖС болуына байланысты қаралып жатқан тікбұрышты импульс уақыттың шын жұп функциясы болып табылады.
Келесі суреттер оның импульсімен АЖС және ФЖС көрсетеді.
Сигнал жұп функция болғандықтан АЖС жұп, ФЖС тақ функция.
Берілген сигналдың спектрі шексіздікке қарай кетеді, біртіндеп өшеді. Сондықтан спектрдің эффектифті ені деген түсінік енгіземіз. Графиктен көрсетілгендей спектр жапырақты сипаттамаға ие және басты жапырақтың ені мынаған тең
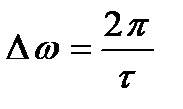
Ал тікбұрышты импульстің ұзақтығы мынаған тең
Спектрлік сигналдың эффективті ені мен сигнал ұзақтығының көбейтіндісі базалық сигнал деп аталады (processing gain).
Бұл қатынастан мынаны көруге болады: сигнал қысқа болған сайын оның спектрі ендірек болады немесе керісінше.Бұл жагдай анықталмағандық қатынас деп аталады.
Тік бұрышты импульс жағдайында:
Екінші мысал. Бір жақты экспоненциалданған импульсті қарастырамыз.
a >0 оң сан.
Тура Фурье түрлендіру арқылы S (w) спектрін есептейміз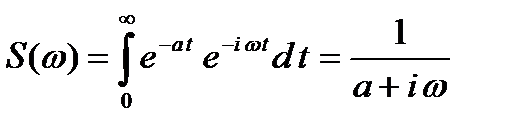 
Келесі сурет экспоненциальды импульс және АЖС және ФЖС көрсетеді
Экспоненциальданған сигналдар үшін сигнал ұзақтығы ретіне уақыт алынады
Спектрдің эффективті енін максимумнан 0.1 деңгейі бойынша аныұтаймыз. Графиктен көрініп тұрғандай бұл ені шамамен мынаған тең
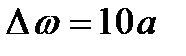
Осылай экспоненциалданған сигналмынаған тең
Үшінші мысал. Периодты сигнал спектрін қарастырамыз. f 1 жиілікке ие гармоникалық сигнал болсын
Эйлер формуласын қолдана отырып осы сигналдың спектрін аламыз
Кейін дельта-функция түріндегі интегралдауда қолданамыз.
Сондықтан сигнал спектрі дельта-функцияның суперпозициясы болады.
Қаралып отырған сигнал шын жұп функция, сондықтан спектрдің жалған бөлігі нөлге тең.
Гармоникалық сигнал ретінде тақ функцияны алайық.
Бұл жағдайда сигнал спектрі мынаған тең.
Қаралып отырған сигнал шын тақ функция, сондықтан спектрдің шын бөлігі нөлге тең. Спектрдің жалған бөлігі суретте келтірілген
Осы сигналдың программасы:
a = 2; %импульстің ұзақтығы(с)
T = 20; %графиктің уақыттық интервалы (c)
dt = 0.1; %уақыттың осі бойынша графиктің қадамы (с)
t = -T/2:dt:T/2; %уақыттың дискреттік моменті(c)
s = rectpuls(t/a); %сигналдың отсеты
figure;
plot(t, s);
axis([-T/2 T/2 0 1.5]);
xlabel('t (c)');
title('Signal s(t)');
grid on;
fb = 2; %графиктің жиіліктік интервалы (Hz)
df = 0.01; %жиіліктің осі бойынша графиктің қадамы (Hz)
f = -fb:df:fb; %жиіліктің дискреттік мағынасы (Hz)
S = i*(-1/2*δ*f+1/2*δ*f)
Ampl = abs(S); %АЖС алу
Re = real(S); %спектрдің шынайы бөлігін алу
Im = imag(S); %спектрдің минимум бөлігін алу
MaxSpectr = max(Ampl); %спектрдің графигі үшін максимумы
figure;
plot(f, Ampl);
axis([-fb fb -1.2*MaxSpectr 1.2*MaxSpectr]);
xlabel('f (Hz)');
title('Spectrum A(f)');
grid on;
figure;
plot(f, Re);
axis([-fb fb -1.2*MaxSpectr 1.2*MaxSpectr]);
xlabel('f (Hz)');
title('Spectrum Re(S(f))');
grid on;
figure;
plot(f, Im);
axis([-fb fb -1.2*MaxSpectr 1.2*MaxSpectr]);
xlabel('f (Hz)');
title('Spectrum Im(S(f))');
grid on;
