”словные законы распределени€
ƒл€ дискретных величин были введены условные веро€тности по формулам
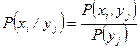 и
и 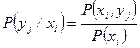 .
.
ƒл€ непрерывных величин аналогично ввод€тс€ плотности дл€ условных законов распределени€
 и
и 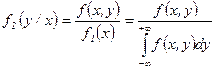 .
.
„исловые характеристики составл€ющих  и
и  двумерной случайной величины
двумерной случайной величины 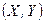 можно найти по формулам
можно найти по формулам
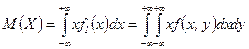 ,
,
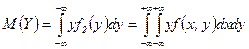 ,
,
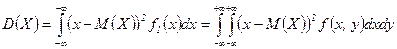 ,
,
 .
.
јналогичные характеристики можно ввести и дл€ условных распределений, например, условные математические ожидани€
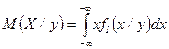 ,
, 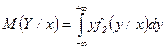 .
.
”словное математическое ожидание 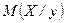 будет функцией от
будет функцией от 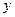 :
:
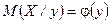 , (1)
, (1)
и наоборот, условное математическое ожидание 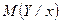 будет функцией от
будет функцией от 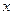 :
:
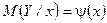 . (2)
. (2)
‘ункции (1) и (2) называютс€ функци€ми регрессии: (1) −  на
на  , а (2) −
, а (2) −  на
на  . √рафики этих функций называютс€ лини€ми регрессии или кривыми регрессии.
. √рафики этих функций называютс€ лини€ми регрессии или кривыми регрессии.
«ависимые и независимые случайные величины
ќпределение. —лучайные величины  и
и  называютс€ независимыми, если условные законы любой из них совпадают с безусловными:
называютс€ независимыми, если условные законы любой из них совпадают с безусловными:
дл€ дискретных случайных величин
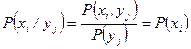 , т.е.
, т.е.  ,
,
дл€ непрерывных
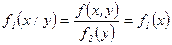 , т.е.
, т.е. 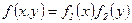 .
.
“аким образом, плотность веро€тности совместного распределени€ системы 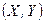 равна произведению плотностей распределени€ составл€ющих. Ёто условие €вл€етс€ не только необходимым, но и достаточным дл€ непрерывных случайных величин. “очнее, имеет место следующа€ теорема.
равна произведению плотностей распределени€ составл€ющих. Ёто условие €вл€етс€ не только необходимым, но и достаточным дл€ непрерывных случайных величин. “очнее, имеет место следующа€ теорема.
“еорема (критерий независимости случайных величин). ƒл€ того, чтобы случайные величины  и
и  были независимыми необходимо и достаточно, чтобы функци€ распределени€ системы
были независимыми необходимо и достаточно, чтобы функци€ распределени€ системы 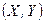 была равна произведению функций распределени€ составл€ющих:
была равна произведению функций распределени€ составл€ющих:
 .
.
роме того, дл€ непрерывных величин это условие равносильно следующему
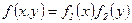 .
.
(ƒоказательство см. в [1].)
ƒл€ независимых случайных величин 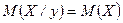 , т.е. функци€ регрессии
, т.е. функци€ регрессии 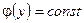 ,
, 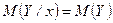 , т.е. функци€ регрессии
, т.е. функци€ регрессии 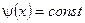 , а значит, линии регрессии −пр€мые, параллельные координатным ос€м.
, а значит, линии регрессии −пр€мые, параллельные координатным ос€м.
ѕример. «адана плотность веро€тности совместного распределени€ системы 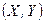
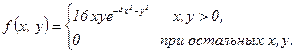
Ќайдем
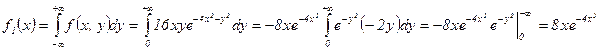 .
.
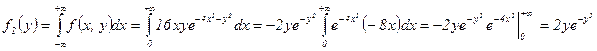 .
.
ћы видим, что 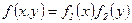 , т.е. случайные величины
, т.е. случайные величины  и
и  €вл€ютс€ независимыми.
€вл€ютс€ независимыми.
овариаци€ (коррел€ционный момент) и коэффициент коррел€ции
ƒл€ двумерной случайной величины 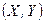 характеристики ее составл€ющих
характеристики ее составл€ющих  и
и 
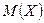 ,
, 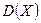 ,
, 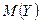 ,
, 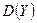 никак не отражают зависимости между
никак не отражают зависимости между  и
и  или ее отсутстви€. ѕоэтому вводитс€ еще одна числова€ характеристика − коррел€ционный момент или ковариаци€.
или ее отсутстви€. ѕоэтому вводитс€ еще одна числова€ характеристика − коррел€ционный момент или ковариаци€.
ќпределение. овариацией или коррел€ционным моментом 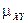 случайных величин
случайных величин  и
и  называетс€ математическое ожидание произведени€ отклонений этих величин от их математических ожиданий:
называетс€ математическое ожидание произведени€ отклонений этих величин от их математических ожиданий:
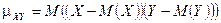 .
.
»спользу€ формулы дл€ математических ожиданий, получаем
дл€ дискретных величин 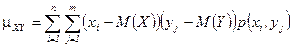 ,
,
дл€ непрерывных величин 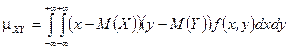 .
.
овариаци€ характеризует зависимость величин.
—войства коррел€ционного момента
1. ƒл€ независимых случайных величин  и
и 
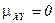 .
.
2. ≈сли 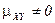 , то случайные величины
, то случайные величины  и
и  зависимы.
зависимы.
3. 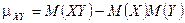 . (ƒл€ доказательства достаточно раскрыть скобки под знаком математического ожидани€ в определении.) ¬ частности
. (ƒл€ доказательства достаточно раскрыть скобки под знаком математического ожидани€ в определении.) ¬ частности
дл€ дискретных величин 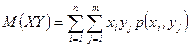 ,
,
дл€ непрерывных величин 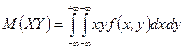 .
.
4. 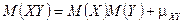 . (—войство сразу вытекает из 3.)
. (—войство сразу вытекает из 3.)
5. 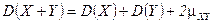 . (¬ыразите дисперсию через математические ожидани€.)
. (¬ыразите дисперсию через математические ожидани€.)
|
|
|
6. 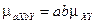 .
.
7. 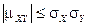 . (ƒоказательство этого свойства можно найти в [1, гл.14, І 17].)
. (ƒоказательство этого свойства можно найти в [1, гл.14, І 17].)
овариаци€ имеет размерность произведени€ размерностей случайных величин  и
и  и зависит от того, в каких единицах измер€лись величины. ƒл€ получени€ безразмерной характеристики вводитс€ пон€тие коэффициента коррел€ции.
и зависит от того, в каких единицах измер€лись величины. ƒл€ получени€ безразмерной характеристики вводитс€ пон€тие коэффициента коррел€ции.
ќпределение. оэффициентом коррел€ции 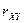 случайных величин
случайных величин  и
и  называетс€ отношение коррел€ционного момента к произведению средних квадратических отклонений этих случайных величин:
называетс€ отношение коррел€ционного момента к произведению средних квадратических отклонений этих случайных величин:
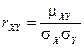 .
.
—войства коэффициента коррел€ции
1. ƒл€ независимых случайных величин  и
и 
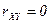 .
.
2. 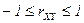 . оэффициент коррел€ции по абсолютной величине не превосходит единицы.
. оэффициент коррел€ции по абсолютной величине не превосходит единицы.
3. ≈сли  , то случайные величины
, то случайные величины  и
и  св€заны линейной зависимостью, т.е.
св€заны линейной зависимостью, т.е. 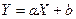 .
.
ќпределение. —лучайные величины  и
и  называютс€ некоррелированными, если
называютс€ некоррелированными, если 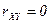 , и коррелированными, если
, и коррелированными, если 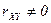 .
.
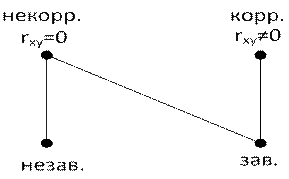
—ледует помнить, что пон€ти€ некоррелированности и независимости не совпадают, несмотр€ на внешнее сходство. Ќезависимые величины − некоррелированные, но обратное неверно. оррелированные величины − зависимые, но обратное неверно. Ћюбые коррелированные величины всегда зависимые, любые независимые величины всегда некоррелированные. Ёто можно отразить на двудольном графе.
ѕример. ” случайных величин  и
и 
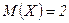 ,
, 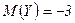 ,
, 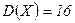 ,
, 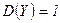 ,
, 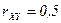 . Ќайдите
. Ќайдите 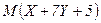 и
и  .
.
–ешение. 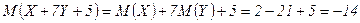 .
.
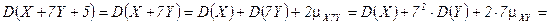
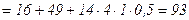 .
.
ќтвет. 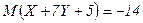 ,
, 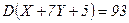 .
.
¬ заключение рассмотрим пример на вычисление всех характеристик системы случайных величин.
ѕример. «адан закон распределени€ системы случайных величин 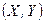 :
:
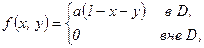

Ќайдите значение параметра 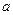 . Ќайдите законы распределени€ составл€ющих
. Ќайдите законы распределени€ составл€ющих  и
и  . Ќайдите условные законы распределени€ составл€ющих. Ќайдите
. Ќайдите условные законы распределени€ составл€ющих. Ќайдите 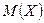 ,
, 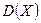 ,
, 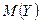 ,
, 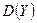 ,
, 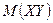 ,
, 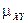 ,
, 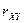 .
.
–ешение. а) —огласно свойству 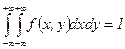 совместной плотности веро€тности
совместной плотности веро€тности 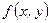 системы случайных величин
системы случайных величин 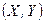 (свойство 4 из І10) дл€ заданной плотности также
(свойство 4 из І10) дл€ заданной плотности также
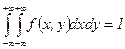 , т.е.
, т.е. 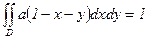 . ¬ычислим интеграл:
. ¬ычислим интеграл:
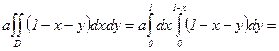
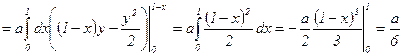 . —ледовательно,
. —ледовательно,  .
.
»так, плотность веро€тности имеет вид
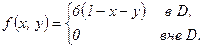
б) «аконы распределени€ составл€ющих  и
и  найдем по формулам:
найдем по формулам:
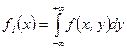 − плотность веро€тности составл€ющей
− плотность веро€тности составл€ющей  и
и
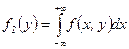 − плотность веро€тности составл€ющей
− плотность веро€тности составл€ющей  .
.
≈сли 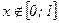 , то
, то 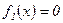 , а при
, а при 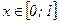
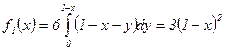 , поэтому
, поэтому
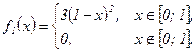
јналогично, если  , то
, то 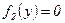 , а при
, а при 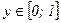
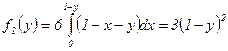 , поэтому
, поэтому
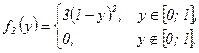
в) ”словные законы распределени€ составл€ющих  и
и  найдем по формулам:
найдем по формулам:
 и
и 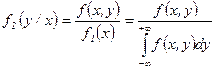 .
.
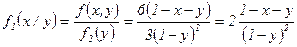 при
при 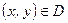 , т.е.
, т.е.
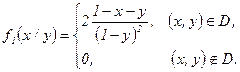
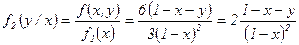 при
при 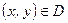 , т.е.
, т.е.
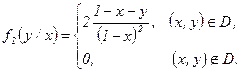
г) ћатематическое ожидание 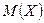 найдем по формуле
найдем по формуле
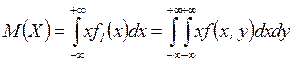 , а т.к.
, а т.к. 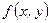 отлична от 0 только в области
отлична от 0 только в области 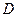 , то
, то
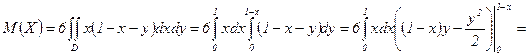
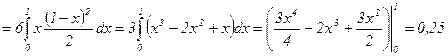 .
.
јналогично, 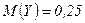 .
.
ƒл€ вычислени€ дисперсии найдем 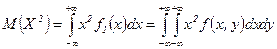 . ј т.к.
. ј т.к. 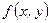 отлична от 0 только в области
отлична от 0 только в области 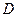 , то
, то
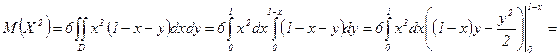
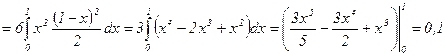 .
.
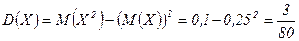 .
.
јналогичные вычислени€ дл€  дают
дают 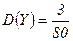 .
.
—редние квадратические отклонени€ 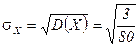 и
и 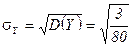 .
.
д) ћатематическое ожидание 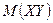 найдем по формуле
найдем по формуле
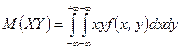 . ј т.к.
. ј т.к. 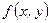 отлична от 0 только в области
отлична от 0 только в области 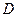 , то
, то
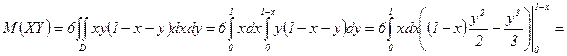
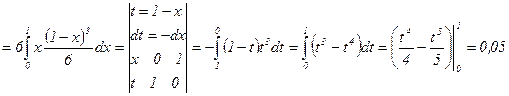 .
.
е) оррел€ционный момент 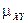 найдем по формуле
найдем по формуле 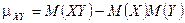 .
.
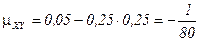 .
.
оэффициент коррел€ции 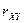 вычисл€етс€ по формуле
вычисл€етс€ по формуле 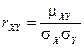 .
.
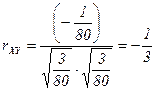 .
.
“ак как коэффициент коррел€ции отличен от 0, случайные величины  и
и  коррелированные, а значит, зависимые.
коррелированные, а значит, зависимые.
ќтвет.  ,
,
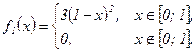 ,
,
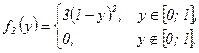
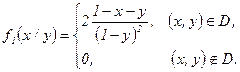
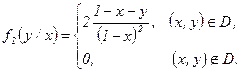
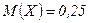 ,
, 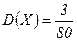 ,
, 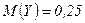 ,
, 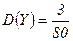 ,
,
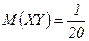 ,
, 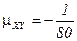 ,
,  .
.
«амечание. —имметричные значени€ дл€ составл€ющих в данном примере получились благодар€ симметричности плотности совместного распределени€ и области 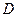 . ¬ общем случае таких совпадений не будет.
. ¬ общем случае таких совпадений не будет.
«акон больших чисел
¬ 1913 г. ¬ –оссии был отмечен необычный юбилей − двухсотлетие закона больших чисел. ¬ 1913 г. Ѕыла переведена на русский €зык Ђ„асть четверта€ сочинени€ я. Ѕернуллиї, опубликованного в 1713 г. через 8 лет после его смерти. —амо название Ђзакон больших чиселї принадлежит ѕуассону (1781 − 1840).
|
|
|
„то такое Ђзакон больших чиселї?
ѕод Ђзаконом больших чиселї в широком смысле слова понимаетс€ общий принцип, согласно которому (по словам ј.Ќ. олмогорова) совокупное действие большого числа случайных факторов приводит к результату, почти не завис€щему от случа€.
¬ узком (математическом) смысле слова закон больших чисел Ц это р€д теорем, в которых при тех или иных услови€х устанавливаетс€ факт приближени€ средних характеристик большого числа испытаний к некоторым определенным посто€нным.
ƒл€ каждой случайной величины нельз€ предвидеть, какое она примет значение в итоге испытани€. Ќо поведение суммы большого числа случайных величин почти утрачивает случайный характер и становитс€ закономерным, здесь необходимое прокладывает себе дорогу сквозь множество случайностей.
»сторически первой формулировкой больших чисел считаетс€ теорема Ѕернулли, опубликованна€ в 1713 г. ¬ дальнейшем были получены более простые еЄ доказательства, основанные на неравенстве „ебышева[1].
“еорема Ѕернулли (современна€ формулировка).
ѕри неограниченном числе испытаний 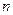 в схеме Ѕернулли относительна€ частота (частость) по€влени€ событи€
в схеме Ѕернулли относительна€ частота (частость) по€влени€ событи€ 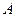 стремитс€ по веро€тности к веро€тности
стремитс€ по веро€тности к веро€тности 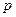 событи€
событи€ 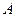 :
:
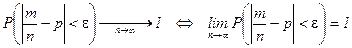 .
.
“еорема (неравенство „ебышева). ƒл€ любого 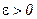 и любой случайной величины
и любой случайной величины  , имеющей математическое ожидание
, имеющей математическое ожидание 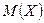 и дисперсию
и дисперсию 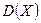 , веро€тность того, что случайна€ величина отклонитс€ от
, веро€тность того, что случайна€ величина отклонитс€ от 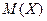 не меньше чем на
не меньше чем на 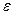 меньше либо равна
меньше либо равна 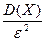 :
:
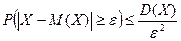 . (1)
. (1)
ƒоказательство (дл€ непрерывной случайной величины): ○
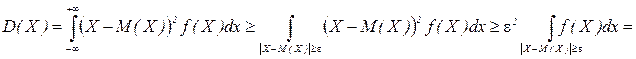
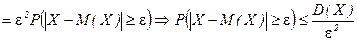 . ●
. ●
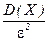 − это верхн€€ граница веро€тности, она может быть достаточно большой, существенно больше 1.
− это верхн€€ граница веро€тности, она может быть достаточно большой, существенно больше 1.
“ак как событи€ 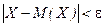 и
и 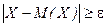 противоположные, то друга€ форма неравенства „ебышева
противоположные, то друга€ форма неравенства „ебышева
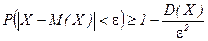 . (2)
. (2)
«десь даетс€ нижн€€ оценка веро€тности рассматриваемого событи€.
ѕример. ƒл€ любой случайной величины  по неравенству „ебышева получаем
по неравенству „ебышева получаем
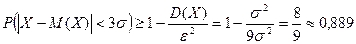 , в то врем€ как дл€ нормально распределЄнной величины
, в то врем€ как дл€ нормально распределЄнной величины 
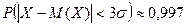 , т. е. оценка по неравенству „ебышева менее точна€, но применима€ дл€ всех без исключени€ случайных величин.
, т. е. оценка по неравенству „ебышева менее точна€, но применима€ дл€ всех без исключени€ случайных величин.
“еорема „ебышева. ≈сли 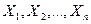 − попарно независимые случайные величины с равномерно ограниченными дисперси€ми, т.е.
− попарно независимые случайные величины с равномерно ограниченными дисперси€ми, т.е. 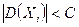 , то при неограниченном увеличении
, то при неограниченном увеличении 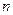 их среднее арифметическое
их среднее арифметическое 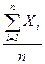 стремитс€ по веро€тности к среднему арифметическому их математических ожиданий:
стремитс€ по веро€тности к среднему арифметическому их математических ожиданий: 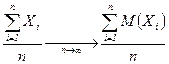 ,
,
т.е. дл€ любого 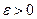
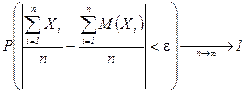 .
.
ƒоказательство. ○ ѕо неравенству „ебышева 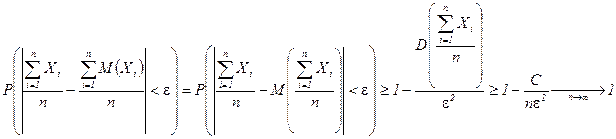 , т.к.
, т.к. 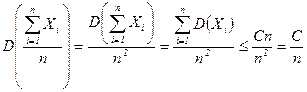 . ●
. ●
“аким образом, при большом числе случайных величин 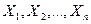 их среднее арифметическое
их среднее арифметическое 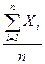 − случайна€ величина, сколь угодно мало отличающа€с€ от посто€нной величины
− случайна€ величина, сколь угодно мало отличающа€с€ от посто€нной величины 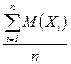 , т.е. практически перестает быть случайной. ¬ частности, если величины
, т.е. практически перестает быть случайной. ¬ частности, если величины 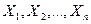 одинаково распределены
одинаково распределены 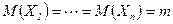 , то
, то 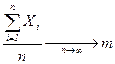 .
.
“еорема „ебышева имеет важное практическое значение: при измерении некоторой величины 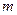 , истинное значение которой неизвестно, провод€т
, истинное значение которой неизвестно, провод€т 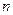 независимых измерений
независимых измерений 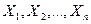 . “огда
. “огда 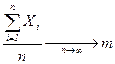 . Ётим обосновываетс€ выбор среднего арифметического в качестве меры истинного значени€
. Ётим обосновываетс€ выбор среднего арифметического в качестве меры истинного значени€ 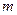 .
.
—мысл теоремы „ебышева заключаетс€ в том, что хот€ отдельные независимые величины могут принимать значени€, далекие от своих математических ожиданий среднее арифметическое большого числа случайных величин с большой веро€тностью принимает значение, близкое к некоторой константе, а именно к 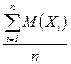 . Ќапример, при измерении физической величины провод€т несколько независимых измерений и их среднее арифметическое принимают в качестве истинного размера.
. Ќапример, при измерении физической величины провод€т несколько независимых измерений и их среднее арифметическое принимают в качестве истинного размера.
числу теорем закона больших чисел относитс€ и центральна€ предельна€ теорема Ћ€пунова[2]
“еорема (центральна€ предельна€ теорема Ћ€пунова). –аспределение суммы 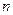 попарно независимых случайных величин
попарно независимых случайных величин 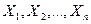 приближаетс€ к нормальному, если:
приближаетс€ к нормальному, если:
1. все эти величины имеют конечные математические ожидани€ и дисперсии
2. ни одна из величин по своим значени€м резко не отличаетс€ от остальных.
ѕример. ¬ университете, куда ежедневно приход€т 6400 студентов, имеетс€ 2 входа. аждый студент с веро€тностью 0,5 заходит в любой из них и сдает пальто в соответствующий гардероб. —колько вешалок должно быть в каждом гардеробе, чтобы с веро€тностью, большей 0,997 их хватило?
|
|
|
–ешение. — каждым студентом св€жем случайную величину 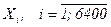 , котора€ примет значение 1, если студент заходит с первого входа и 0 в противном случае. “огда количество студентов, зашедших с первого входа и сдающих пальто в соответствующий гардероб, равно
, котора€ примет значение 1, если студент заходит с первого входа и 0 в противном случае. “огда количество студентов, зашедших с первого входа и сдающих пальто в соответствующий гардероб, равно 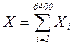 . «аконы распределени€ составл€ющих, очевидно, таковы
. «аконы распределени€ составл€ющих, очевидно, таковы
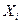
| ||
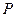
| 0,5 | 0,5 |
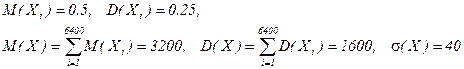
“ак как сумма большого числа одинаково распределенных величин по теореме Ћ€пунова подчин€етс€ нормальному закону распределени€, то 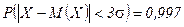 , поэтому достаточно вешалок в промежутке
, поэтому достаточно вешалок в промежутке 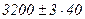 , т.е.
, т.е. 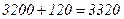 .
.
ќтвет. 3320 вешалок.
[1] ѕафнутий Ћьвович „ебышЄв (1821 −1894) − русский математик и механик, его работы по теории веро€тностей имели огромное значение дл€ развити€ математики.
[2] јлександр ћихайлович Ћ€пунов (1857 − 1918) − русский математик и механик, выдающийс€ представитель петербургской математической школы, созданной ѕ.Ћ. „ебышевым.






