Перенос массы
Вывод уравнения неразрывности для многокомпонентной среды.
Уравнение выводится из закона сохранения массы i компонента.Если процесс идет с химическим превращением, то появляется удельный источник (сток) массы i компонента 
 :
:
 [
[  dV]=
dV]=  dV
dV
 +div(
+div(  )=
)= 
Пусть имеем n-компонентов:
 +div(Σ
+div(Σ  )] =
)] =  = >
= >  – т.е. переходит в уравнение неразрывности для однокомпонентной среды.
– т.е. переходит в уравнение неразрывности для однокомпонентной среды.
 =0- по закону сохранения массы при химических превращениях.
=0- по закону сохранения массы при химических превращениях.
Введем скорость центра масс:
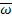 ==
==  =
=  =>
=>  =
=  =
= 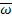 ρ
ρ
 =
=  - поток массы i компонента
- поток массы i компонента
 +div(
+div(  )-div(
)-div(  )+ div(
)+ div(  )=
)=  +div[
+div[  (
(  + div(
+ div(  )=
)=  + div(
+ div(  )+div
)+div  =
=  - уравнение неразрывности для i компонента.
- уравнение неразрывности для i компонента.
Суммируем уравнения неразрывности для всех компонентов:
 + div(
+ div(  )+divΣ
)+divΣ  =Σ
=Σ 
𝛴  =
= 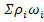 -
-  =0; Σ
=0; Σ 
Получим:
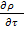 + div
+ div  =0 –уравнение неразрывности для однокомпонентной среды
=0 –уравнение неразрывности для однокомпонентной среды

 +div(
+div( 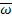 ρ)=0 - уравнение неразрывности для многокомпонентной среды
ρ)=0 - уравнение неразрывности для многокомпонентной среды
 + div(
+ div(  )=
)=  - div
- div 
Вывод уравнения концентрации
 =
=  =>
=>  =
=  – концентрация (массовая или мольная). Тогда из уравнения неразрывности для многокомпонентной среды получаем:
– концентрация (массовая или мольная). Тогда из уравнения неразрывности для многокомпонентной среды получаем:
ρ[  +
+ 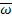 grad
grad  ]+
]+ 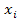 [
[  +div
+div  ]=- div
]=- div  =
= 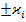 -div
-div 
 =[
=[ 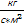 ]=
]= 
µ=f(T,P,U, 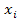 )-химический потенциал. Это работа образования одного моля i-компонента.
)-химический потенциал. Это работа образования одного моля i-компонента.
 - поток химического потенциала i-компонента.
- поток химического потенциала i-компонента.
 =ρ[
=ρ[  (
(  )∇
)∇ 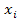 +
+  (
(  ) ∇
) ∇  +
+  (
(  ) ∇
) ∇  +
+  ∇U+…]
∇U+…]
=ρ[  ∇
∇ 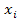 +
+  ∇T+
∇T+  ∇P+
∇P+  ∇U]=ρ[∇
∇U]=ρ[∇ 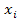 +
+ 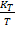 ∇T+
∇T+  ∇P+
∇P+  ∇U], где
∇U], где  - коэффициенты диффузии, термодиффузии, бародиффузии, электродиффузии;
- коэффициенты диффузии, термодиффузии, бародиффузии, электродиффузии; 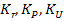 - термо, баро, электродифузиозные коэффициенты- результат нормирования соответствующих коэффициентов различных видов диффузии i компонента
- термо, баро, электродифузиозные коэффициенты- результат нормирования соответствующих коэффициентов различных видов диффузии i компонента 
 =
=  ;
;  =
= 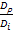 ;
;  =
= 
Выражение учитывает сумму потоков массы i компонента, вызванных изменением концентраций температур, давлений, электрических потенциалов и т.д.
ρ[ 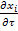 +
+ 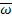 grad
grad  ]= -ρdiv[
]= -ρdiv[  ∇
∇ 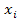 +
+  ∇T+
∇T+  ∇P+
∇P+ 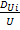 ∇U]
∇U] 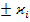 -уравнение концентрации для i компонента
-уравнение концентрации для i компонента
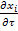 +
+  +
+  +
+  = -
= -  [
[ 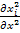 +
+  +
+ 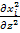 ]
]  - частный случай уравнения концентрации i компонента для изотропных условий и в пренебрежении другими видами диффузии в декартовой системе координат (уравнение Фика).
- частный случай уравнения концентрации i компонента для изотропных условий и в пренебрежении другими видами диффузии в декартовой системе координат (уравнение Фика).
В частном случае для стационарного диффузиозного (молекулярного) переноса массы имеем:
div(-  grad
grad  )=0
)=0
-  grad
grad  =const-закон Фика
=const-закон Фика
 =-
=-  grad
grad  -удельный объемный поток i компонента
-удельный объемный поток i компонента
 =-
=-  grad
grad  - удельный массовый поток i компонента
- удельный массовый поток i компонента
 =𝛽△
=𝛽△  = -
= -  grad
grad  =-
=-  => 𝛽 =
=> 𝛽 =  - коэффициент массоотдачи. Получен по аналогии с коэффициентом теплоотдачи. Удельный объемный поток i-го компонента.
- коэффициент массоотдачи. Получен по аналогии с коэффициентом теплоотдачи. Удельный объемный поток i-го компонента.
Теория подобия в процессах переноса массы.
 +
+ 
Введем безразмерные параметры:  , где xi0, ω0, z0-характерные параметры.
, где xi0, ω0, z0-характерные параметры.
 +
+ 
Нормируем комплексы характерных параметров при всех членах уравнения по комплексу параметров при диффузионном члене:
 +
+ 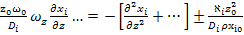
Fo д=  - диффузионный критерий Фурье (мера нестационарности процесса);
- диффузионный критерий Фурье (мера нестационарности процесса);
Peд=  - диффузионный критерий Пекле (соотношение конвективного и диффузионного переноса массы) Peд=
- диффузионный критерий Пекле (соотношение конвективного и диффузионного переноса массы) Peд= 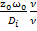 =Re Prд, где Prд=
=Re Prд, где Prд= 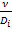 - диффузионный критерий Прандтля.
- диффузионный критерий Прандтля.
Po=  - соотношение источника (стока) массы к диффузионному переносу. Дефузионный критерий Померанцева.
- соотношение источника (стока) массы к диффузионному переносу. Дефузионный критерий Померанцева.
 +…=-
+…=- 
Из граничного условия аналогичного условию III рода в теплообмене получаем диффузионный критерий Био: Biд= 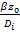 .
.
β[xi(τ,0)-xi]=  ; β
; β  [xi(τ,0)-xi]=
[xi(τ,0)-xi]=  ; Biд[xi(τ,0)-xi]=
; Biд[xi(τ,0)-xi]= 






