Конвективный перенос тепла.
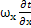 =0, для Pe →
=0, для Pe → 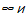 Re→
Re→  .Возникающий парадокс разрешим в приближении пограничного слоя.
.Возникающий парадокс разрешим в приближении пограничного слоя.
Уравнение Фурье-Кирхгофа в безразмерной форме имеет вид:
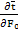 +Pe
+Pe 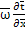 =
= 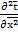 +Po
+Po
-λ 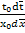 =α
=α 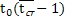 - граничное условие 3 рода в безразмерной форме для пограничного слоя(
- граничное условие 3 рода в безразмерной форме для пограничного слоя( -характерная температура в потоке):
-характерная температура в потоке):
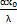 (
(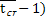 =-
=-  -=>Nu(
-=>Nu(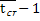 )=-
)=- 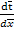
ρ[ 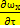 +
+  …]=-
…]=- 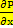 – ρg+µ[
– ρg+µ[  +….] - уравнение Навье-Стокс
+….] - уравнение Навье-Стокс
β=-1 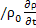 - коэффицент объемного расширения 1/[град].
- коэффицент объемного расширения 1/[град].
Если ρ лишь функция t,то:
β=-1 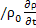
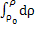 =-β
=-β 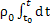 =>ρ=
=>ρ= 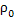 - β
- β 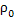 (t-
(t-  )
)
ρ[ 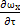 +
+ 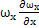 …]=-
…]=- 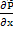 + β
+ β 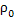 (t-
(t-  )g+μ[
)g+μ[ 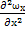 +
+ 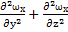 ],где
],где 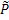 =Р+
=Р+ 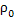 gx-приведенное давление.
gx-приведенное давление.
ρ[ 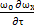 +
+ 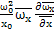 ]=-
]=- 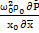 +
+  g+ µ
g+ µ 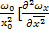 +…]
+…]
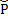 =
= 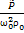 - безразмерное приведенное давление
- безразмерное приведенное давление
Нормируем все члены уравнения по характерным параметрам при конвективном члене:
 ρ[
ρ[ 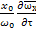 +
+ 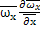 +…]=-
+…]=- 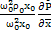 +
+ 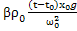 +µ
+µ 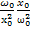 [
[ 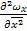 +….]
+….]
Полагая в приближении Буссинеска ρ= 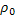 ,имеем:
,имеем:
 [
[ 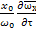 +
+ 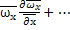 ]=-
]=-  +
+ 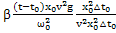 +µ
+µ 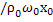 [
[ 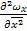 +….]
+….]
1/Pe  +
+ 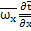 =
= 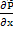 +
+ 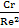 +
+  [
[ 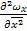 ….], где Gr=
….], где Gr= 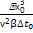 - критерий Грасгофа(соотношение сил веса и подъемной силы за счет зависимости плотности от температуры в неизотермических условиях к силе трения),
- критерий Грасгофа(соотношение сил веса и подъемной силы за счет зависимости плотности от температуры в неизотермических условиях к силе трения), 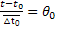 - безразмерный перепад температур.
- безразмерный перепад температур.
Система уравнений гидродинамики и переноса тепла в приближении температурного пограничного слоя в безразмерном (критериальном виде)
Nu=f(Re,Gr,Pe,Fo)
Уравнение стационарного конвективного переноса в критериальном виде, памятуя о том, чтоPe=Re*Pr
Nu=f(Re,Pr,Gr)-оно используется для определения коэффициента теплопередачи, т.к. Nu= 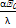
Возможно 2 вида конвекции: вынужденная(за счет действия внешних сил) и естественная (за счет действия внутренних сил, возникающих в неизотермической системе за счет зависимости плотности от температуры).Естественная конвекция возможна при определенных условиях:
Толщина теплового пограничного слоя. Закон ее изменения по длине.
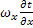 +
+ 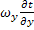 =
=  - уравнение переноса тепла в плоском стационарном погрпничном слое.
- уравнение переноса тепла в плоском стационарном погрпничном слое.
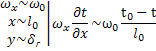

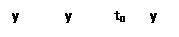
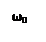



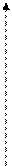

 +
+  =0
=0
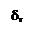




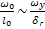

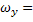





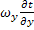 =
= 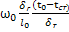 =0; т.к.
=0; т.к. 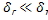

 =
= 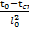 <
< 
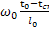 = a
= a  =>
=>
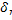 =
= 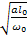 =>
=>  =
= 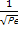 =
= 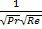 =
=  =>
=>  =
= 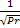 , т.к.
, т.к. 
Из полученного выражения  =
= 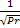 можно сделать выводы:
можно сделать выводы:
1)По одному и тому же закону изменяются  и
и 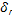 , т.е.
, т.е. 
2)Pr<1,т.е. v<a, что характерно для расплавов металлов.
Решение задачи о переносе тепла в температурном пограничном слое дает зависимость для расчета коэффициента теплоотдачи:
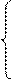
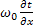 =a
=a 
Y=0, t= 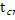 , y=
, y= 
U= 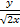
Nu=0,377 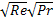 =C
=C  , при m=n=1/2.
, при m=n=1/2.



 Y y
Y y 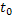 y
y 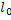
 | |||
 | |||

 δг
δг
 δт
δт

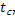 t
t 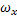 x
x
Из подобия треугольников:
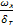 =
= 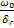 =>
=> 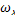 =
= 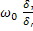
Текущее значение 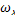 также из подобия треугольников равно:
также из подобия треугольников равно:
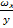 =
= 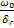 =>
=> 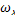 =f(y)=
=f(y)= 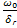 y=
y= 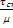 y=
y=  , т.к. поле скоростей в вязком слое вблизи стенки равно:
, т.к. поле скоростей в вязком слое вблизи стенки равно:
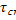 =μ
=μ 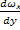 =>
=> 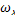 =
= 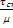 y;
y;  ωх=f(y). Значит
ωх=f(y). Значит 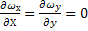 , т.е. ωy=const=0 из условий непроницаемости пластины, которую обтекает жидкость
, т.е. ωy=const=0 из условий непроницаемости пластины, которую обтекает жидкость
Подставляя полученное выражение для 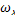 в уравнение переноса тепла в пограничном слое, получаем:
в уравнение переноса тепла в пограничном слое, получаем:
 = a
= a  =>
=>
 =
= 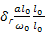 =
=  =
= 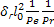 =
= 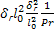 =>
=> 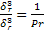 , т.к.
, т.к. 
 =
= 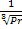 .
.
Полученная зависимость подтверждает ранее сделанный вывод:
1)зависимость 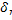 =f(x) следует тому же закону, что и
=f(x) следует тому же закону, что и 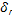 =f(x), т.е.
=f(x), т.е. 
2)Pr>1;v>а, что характерно для вязких неметаллических сред.
Решение задачи о переносе тепла в температурном пограничном слое дает зависимость для расчета коэффициента теплоотдачи:
 y
y  =
= 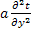
t= 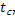 ; у=
; у=  ; t=
; t= 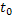 ;
;
Подстановка u= 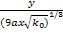
Решение получаем в виде:
Nu=0,2224  = C
= C  , где m=1/2, n =1/3.
, где m=1/2, n =1/3.
Естественная конвекция
Конвективное движение в системе возникает за счет внутреннего побудителя движения (зависимости плотности среды от температуры и изменения температуры по толщине слоя).
Условия возникновения естественной конвекции.
Если вектор силы F возникающей при перемещении объема V в поле температур будет направлен вверх, то система по теореме Ляпунова неустойчива, ибо амплитуда бесконечно малого возмущения, внесенного в систему, будет расти. В противном случае система устойчива. В первом случае возникает естественная конвекция. Во втором не возникает.






Холодная область
Уст.

 Неуст.
Неуст.
Горячая область
 t
t
dF=Vgdρ=Vg  dz=-Vgβ
dz=-Vgβ 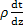 dz
dz
т.к. β=-  ; ρ0 –характерная плотность.
; ρ0 –характерная плотность.
dt/dz>0,dF<0-система устойчива
 <0,dF>0 – система неустойчива
<0,dF>0 – система неустойчива
 Оценка скорости естественной конвекции.
Оценка скорости естественной конвекции.
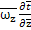 =-
=- 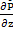 +
+ 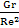 △
△ 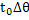 +1/Re
+1/Re 
1. Гравитационно-инертный режим (первый предельный режим естественной конвекции):
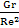 =0=>Gr=
=0=>Gr= 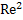 =>Re
=>Re  =>
=> 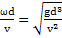 β△
β△  =>ω=
=>ω= 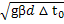 т.е. ω
т.е. ω 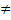 f(ν)
f(ν)
2. Гравитационно-вязкостной режим (второй предельный режим):
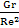 =1=>Gr=Re
=1=>Gr=Re  =
=  β△
β△ 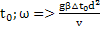 , т.е. ω=f(ν)
, т.е. ω=f(ν)
Оценка коэффициента теплоотдачи при естественной конвекции:
Ранее было показано, что для конвективного переноса тепла характерно:
Nu= C  выражаем критерий Re через критерий Gr.
выражаем критерий Re через критерий Gr.
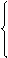
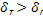 c
c 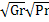 -гравитационно-вязкостной режим
-гравитационно-вязкостной режим
Nu= 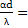 c
c 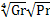 -гравитационно-инерционный режим
-гравитационно-инерционный режим

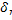 <
< 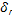 c
c 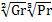 - гравитационно-вязкостной режим
- гравитационно-вязкостной режим
c  - гравитационно-инерционный режим
- гравитационно-инерционный режим
Экспериментальные данные принято обрабатывать зависимостью Nu =c  , где n=1/4 в большинстве случаев.
, где n=1/4 в большинстве случаев.
Для вертикальной пластины:
Nu=0,55 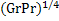 , при 2*
, при 2*  <GrPr<
<GrPr< 
Для горизонтальной трубы:
Nu=0,41 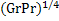 , при GrPr>
, при GrPr> 
Неизотермичность 









 течения может сказаться на профиле скоростей в потоке:
течения может сказаться на профиле скоростей в потоке:
Изотермическое течение неизотермическое течение



 r r
r r
t
 t
t






