Задача №1. Изобразить проектными горизонталями поверхность.
h=0,2м
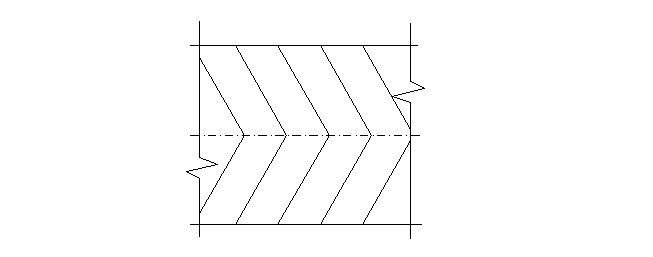
Задача №2. Нахождение проектной отметки точки на прямой.
Исходные данные:
 =100,4
=100,4
 =100,7
=100,7
 =100,51
=100,51
 ;
;
 =16,87
=16,87

Можно найти место положение точки графически для этого в точках А и В в противоположных направлениях строят перпендикуляры к отрезку AB на которых в произвольном масштабе откладывают превышение точек А и В относительно С и искомая точка С получится на пересечении с отрезком АВ линии проходящей через окончание перпендикуляров.
Задача №3. Градуирование прямой.
a) Исходные данные: известны отметки начала и окончания отрезка А и В и расстояние между ними.
 =110,81
=110,81
 =112
=112
l =145
h=0,2м

Находим уклон АВ
 ;
;
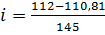 =0,0082
=0,0082
Ближайшая к точки А горизонталь имеет отметку 111. Чтобы найти ее местоположение необходимо найти превышение между точкой А и горизонталью 111
 =111-110,81=0,19 м
=111-110,81=0,19 м
Зная превышение  и уклон
и уклон  находим величину заложения проектной горизонтали
находим величину заложения проектной горизонтали  .
.
 =
= 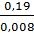 =23,75 м
=23,75 м
Аналогично ищем заложение горизонтали ближайшей к точке В, то есть  .
.
 =
= 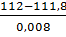 =25 м
=25 м
Заложение между остальными проектными горизонталями 
 =
=  =25м
=25м
Остальные проектные горизонтали будут повторятся.
б) Исходные данные: известны уклон и отметка одной точки. Ближайшей точки А проектной горизонтали.

 =112
=112
h=0,1
Находим местоположение ближайшей к точке проектной горизонтали 111,9
 =
= 
 2,08
2,08
Далее находим заложение горизонталей.
Остальные проектные горизонтали откладываем на таком же расстоянии.

Задача №4. Найти отметку точки, лежащей на красной линии квартала.
Исходные данные:
 =15
=15 
 =20
=20 
 =10
=10 
 м
м
 =3,0 м
=3,0 м
 =6,0 м
=6,0 м
l =110 м
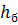 =0,1 м
=0,1 м

В проектах застройки M 1:500 должны быть указаны отметки всех характерных точек поверхности, а именно в местах резкого изменения продольных уклонов улиц, в местах пересечения осей улиц и углов кварталов по красной линии. Отметки точек по красной линии улиц легко найти последовательно определяя отметки характерных точек поперечного профиля улицы (1, 2, 3) в сечении проходящем через точку отметку которой необходимо найти (А).
 =H+
=H+  =122,68+1,1=123,78 м
=122,68+1,1=123,78 м
 >H
>H
 =
=  -
- 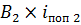 =123,78
=123,78  6
6  0,015=123,69
0,015=123,69

 =
=  +
+ 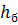 =123,69+0,1=123,79
=123,69+0,1=123,79
 =
=  =123,79+3
=123,79+3  0,02=123,85
0,02=123,85
С такой задачей встречаются при частичном преобразовании рельефа, то есть при строительстве отдельных объектов. Отметки точек красных линий являются опорными при определении отметок планируемого участка, примыкающего к красной линии.
Задача №5. Уравновешивание отметки угла квартала.
Исходные данные:
H=59,4 м
 =36
=36 
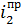 =56
=56 
 =18
=18 
 =16
=16 
 =12 м
=12 м
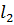 =14 м
=14 м
 =15 м
=15 м
 =17 м
=17 м
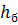 =0,09 м
=0,09 м


Определяем отметку точки А, то есть отметку угла квартала, последовательно. Исходя из поперечных профилей обеих улиц. Но в этом случае получим два значения отметки точки А: -по профилю улицы I; -по профилю улицы I I;. Сопоставляя полученные два значения находим третье обеспечивающее допустимые уклоны тротуарных полос обеих улиц. Проводим линии сечений через точку А. Отметки на оси улицы I в створе красных линий (т.е. по линии соединяющей углы кварталов).
 =H-(
=H-( +
+  =59,4-(15+17
=59,4-(15+17  0,036=58,248
0,036=58,248
Выполняем аналогичные вычисления на улицы II:
 =H-(
=H-(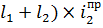 =59,4-(12+14
=59,4-(12+14  0,056=57,944
0,056=57,944
Отметки обозначенных на рисунке точек (3-6) определяем с учетом их превышений относительно осей улиц.
Считаем отметки по профилю улицы I:
 =
=  =58,248
=58,248  14
14  0,016=58,024
0,016=58,024
 =
= 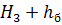 =58,024+0,09=58,033
=58,024+0,09=58,033
 =
= 
Определяем отметки по поперечному профилю II улицы:
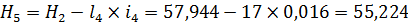


Предварительно примем за проектную наибольшую из полученных высот точек А, тогда поперечный уклон тротуара улиц в сечение улицы II будет равен:


Принимаем полученную отметку точки А за проектную то есть  =193
=193  Поперечный уклон тротуара получился допустимым по нормативным требованиям.
Поперечный уклон тротуара получился допустимым по нормативным требованиям.






