Звук может использоваться в качестве термометра, так как его скорость пропорциональна квадратному корню температуры. Этот метод без инерционен, позволяет отмечать колебания температуры 0.05 К, что недоступно жидкостным и ртутным термометрам. Помещенный на метеорологический зонд, поднимающийся с большой скоростью, термометр успевает фиксировать изменения температуры с точностью 0.05К.К примеру, скорость звука в воздухе при 0ºС составляет 331 м/с, при 20ºС – 343м/с.
2.4. Уравнение любой волны является решением волнового уравнения. Пусть в положительном направлении оси X распространяется плоская монохроматическая волна.
Тогда  (
( ) = Acos (
) = Acos ( t-kx+j), следовательно
t-kx+j), следовательно
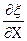 = -A ksin (
= -A ksin ( t-kx+j),
t-kx+j), 
 =-k
=-k  Acos (
Acos ( t-kx+j),
t-kx+j),  = -A w sin(ωt+φ)
= -A w sin(ωt+φ)
 -
-  A cos (
A cos ( t-kx+j). Из сопоставления вторых производных получим
t-kx+j). Из сопоставления вторых производных получим
 =
=  ,
,  =
= 
 , т.е. множитель перед
, т.е. множитель перед 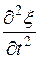 определяет квадрат скорости волны.
определяет квадрат скорости волны.
Уравнение любой волны является решением соответствующего волнового уравнения, получающегося из ньютоновского рассмотрения движения малого элемента среды. Так, плоская волна, распространяющаяся в газе в направлении оси Х, является решением уравнения  =
= 
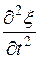 .
.
Для волны, распространяющейся в произвольном направлении, волновое уравнение должно связывать производные по Х,Y,Z,t соответствующим образом.  +
+  +
+  =
= 
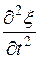 , или
, или  =
= 
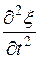 , где
, где
 =
=  +
+  +
+  - оператор Лапласа. Если такое уравнение в некоторой системе связывает пространственные и временные производные, то
- оператор Лапласа. Если такое уравнение в некоторой системе связывает пространственные и временные производные, то
это однозначно указывает на то, что в среде распространяется волна  (
( ) = Acos (
) = Acos ( t-kx+j). Так, волновое уравнение для электромагнитной волны, распространяющейся в вакууме имеет вид
t-kx+j). Так, волновое уравнение для электромагнитной волны, распространяющейся в вакууме имеет вид  E =
E = 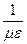
 ,
,  H =
H = 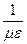
 .
.
2.5. Энергия упругой (механической) волны.
Пусть в некоторой среде в направлении оси Х распространяется плоская продольная волна  (x,t) = Asin (
(x,t) = Asin ( t-kx+j). Выделим в среде малый элемент объема
t-kx+j). Выделим в среде малый элемент объема  , настолько малый, чтобы деформацию и скорость движения во всех точках этого объема можно было считать одинаковыми и равными соответственно
, настолько малый, чтобы деформацию и скорость движения во всех точках этого объема можно было считать одинаковыми и равными соответственно 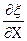 и
и  . Выделенный объем обладает кинетической энергией
. Выделенный объем обладает кинетической энергией 


 =
=  (
( )
)  , аналогично
, аналогично 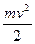
( -масса объема,
-масса объема,  - его скорость). Потенциальная энергия упругой деформации этого объема
- его скорость). Потенциальная энергия упругой деформации этого объема


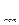 =
= 
 =
=  (
(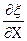 )2∆V
)2∆V
где Е – модуль Юнга, e = 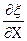 - относительная деформация.
- относительная деформация.
Полная энергия этого объема равна

 полная =
полная = 

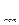 +
+ 

 =
=  A
A 
 cos
cos  (
( t-kx+j) +
t-kx+j) + 
 A
A  cos
cos  (
( t-kx+j) = A
t-kx+j) = A 
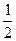 cos
cos  (
( t-kx+j)
t-kx+j)  (rw
(rw  +Ek
+Ek 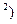 = A
= A  cos
cos  (
( t-kx+j)
t-kx+j)  rw
rw  .
.
Разделив это значение на  , получим объемную плотность энергии волны
, получим объемную плотность энергии волны
 = w
= w 
 = A
= A  cos
cos  (
( t-kx+j)rw
t-kx+j)rw  = A
= A  rw
rw 
 .
.
Плотность энергии в каждый момент времени в разных точках пространства различна. Среднее значение плотности энергии в точке пространства получим, усреднив данное выражение по времени с учетом того, что среднее значение от cos  равно нулю.
равно нулю.
<w>  = A
= A  rw
rw 
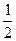 =2π2A2rf
=2π2A2rf  .
.
Среднее значение плотности энергии в данной точке среды пропорционально квадрату амплитуды, частоты и пропорциональна плотности среды ρ.Такая зависимость характерна для всех видов волн (плоских, сферических, затухающих…).

Итак, среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется в разные точки среды самой волной. Для характеристики этого процесса вводят понятие потока энергии.
Поток энергии Ф ( ) через некоторую поверхность S определяется как энергия, переносимая за единицу времени через эту поверхность. Поток- величина скалярная и измеряется в ваттах (Вт = 1Дж/с). Поток энергии может быть различен через разные элементы поверхности, поэтому для характеристики распределения потока через поверхность вводят понятие плотности потока энергии
) через некоторую поверхность S определяется как энергия, переносимая за единицу времени через эту поверхность. Поток- величина скалярная и измеряется в ваттах (Вт = 1Дж/с). Поток энергии может быть различен через разные элементы поверхности, поэтому для характеристики распределения потока через поверхность вводят понятие плотности потока энергии  . Плотность потока – величина векторная. Вектор
. Плотность потока – величина векторная. Вектор  сонаправлен вектору скорости волны. Тогда поток через малую поверхность dS определяется как d Ф =
сонаправлен вектору скорости волны. Тогда поток через малую поверхность dS определяется как d Ф = 
 = J dS cos (
= J dS cos ( ,
,  ), где
), где  параллелен нормали к поверхности
параллелен нормали к поверхности  . Плотность потока численно равна энергии, переносимой через единицу поверхности, расположенной перпендикулярно направлению переноса энергии, за единицу времени и измеряется в Вт/м
. Плотность потока численно равна энергии, переносимой через единицу поверхности, расположенной перпендикулярно направлению переноса энергии, за единицу времени и измеряется в Вт/м  . Плотность потока может быть разной в разных точках пространства, через которое волна проходит. Тогда поток через поверхность S равен Ф=∫ j d S.
. Плотность потока может быть разной в разных точках пространства, через которое волна проходит. Тогда поток через поверхность S равен Ф=∫ j d S.


Рис.
В оптике, акустике часто используют величину интенсивност и волны I. Она определяется как средняя по времени мощность, переносимая через единицу площади поверхности, перпендикулярной направлению потока.
I = 
 v =
v = 

 =
= 

<w> =2π2A2f2
Интенсивность волны пропорциональна квадрату амплитуды волны
I = <w>v = 2π2  A
A 
 f
f  v. Если источник точечный, то энергию, переносимую через поверхности разных радиусов можно считать постоянной, а интенсивность будет убывать с расстоянием обратно пропорционально r
v. Если источник точечный, то энергию, переносимую через поверхности разных радиусов можно считать постоянной, а интенсивность будет убывать с расстоянием обратно пропорционально r  , так как I
, так как I  S
S  = I1S1, где S
= I1S1, где S  = 4πR
= 4πR 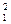 = 4πR
= 4πR  и I
и I  = I
= I 

 .
.
2.7. Волны любой природы (механические, электромагнитные) могут
1) поглощаться в среде
2) отражаться и преломляться на границе двух сред,
3) накладываться друг на друга (принцип суперпозиции), проявляясь в явлениях дифракции и интерференции.
2.7.1. Поглощение волн в среде.
При распространении волны в среде энергия колебательного движения частично переходит во внутреннюю энергию частиц среды – в «тепло». Колебания частиц являются затухающими и плотность потока энергии w, переносимая волной, уменьшается по экспоненциальному закону
w = w0 e -αx,
где α - коэффициент поглощения (см. таб. 1), x -расстояние от границы среды до точки, где определяется поток.
Таблица 1. Значения коэффициентов поглощения звука для различных материалов.
Материал коэффициент поглощения
Бетон 0.015
Оштукатуренная кирпичная стена 0.025
Ковер 0.2
Войлок (2.5 см) 0.78






