Порядок выполнения работы. Негосударственное образовательное учреждение

Негосударственное образовательное учреждение

Высшего профессионального образования

Русско-Британский Институт Управления

(НОУВПО РБИУ)

Кафедра менеджмента

Факультет заочного обучения

Т.А. Шмонова

КОНТРОЛЬНАЯ РАБОТА

По дисциплине «Управление качеством»

1. Описать вид деятельности организации в которой Вы работаете. Как отслеживается или контролируется качество продукции или услуг этой организации. Оценить уровень качества. Обосновать оценку. Какие проблемы в области качества существуют в исследуемой организации? Предложить возможные пути их решения.

Существует ли система менеджмента качества на Вашем предприятии? Если есть, то как ее внедрение повлияло на качество продукции или услуг и на статус организации в целом: появились ли новые выгодные заказы? Если нет, то каковы перспективы ее создания.

Исследование качества продукции методами статистического анализа

Цель работы.

Ознакомление с теоретическими предпосылками, положенными в основу методов статистического анализа и их практического при­менения для исследования качества деталей.

Порядок выполнения работы.

1. Исходные данные для исследования партии деталей по вариантам находятся в таблице 7 и Приложении 1.

2. Определить объем выборки (формула 1).

3. Взять из данных по партии выборку требуемого объема.

4. Обработать статистические данные и вычислить характеристи­ки распределения (табл. 2-6).

6. Вычертить эмпирическую кривую распределения.

7. Определить критерий согласия, построить график теоретичес­кого распределения и сравнить его с экспериментальной кривой распределения (формулы 8,9).

8. Определить вероятный процент брака и годных деталей в партии исследуемых деталей (формулы 10 - 12).

9. Сформулировать выводы и предложения по результатам исследования.

Взяв выборку из генеральной совокупности и вычисляя статисти­ческие характеристики этой выборки — и S, можно с некоторой приближенностью считать, что эти характеристики по своим величи­нам будут близки к соответствующим параметрам генеральной сово­купности — и , то есть это их оценки.

Если

, ,

где ,Х — среднеарифметические значения случайной величи­ны соответственно в генеральной совокупности и в выборке объема п;

, S — среднеквадратичные отклонения изучаемой величины соответственно генеральной совокупности и в выборке из нее n,

то по заданной точности е и вероятности а приближенного равенства 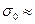S можно определить необходимый объем выборки

(1)

где t определяется в зависимости от вероятности , .

Значения t,a и q определяются номером варианта по табл. 7. По этим величинам опре­деляется объем выборки.

Затем студенты должны измерять параметр X, но результаты измерений этого параметра уже готовы и даны в приложении 1 по вариантам. В каждой выборке 65 измерений, но обработке подлежит выборка, т.е. количество измерений рассчитанное по формуле (1)

Далее необходимо обработать статистические данные (т.е. результаты измерений). Находим наибольшее Х_max и наименьшее Х_min значения наблюдаемого пара­метра X.

Размах варьирования или широта распределения при этом со­ставляет

X_max- X_min (2)

Задав число интервалов п (т= 7 при n = 5 – 100, m=9 – 15 при n > 100), (в нашем случае m=7) определяем цену интервала:

(3)

Цена интервала должна быть больше (или равна) цены деления шкалы измерительного инструмента или прибора, что компенсирует погрешность измерения. Подсчет частот по каждому интервалу удобно производить следующими способами. Слева выписывают ин­тервалы от X_min до

X_min + C; от X_min + C до X_min + 2Cи тд. В каждый ин­тервал включают размеры, лежащие в пределах от наименьшего зна­чения интервала включительно, до наибольшего значения интервала, исключая его. Справа при помощи черточек подсчитывают число размеров по интервалам (табл. 1).,

 

Таблица 1