объёма 
:
частичный интервал 3-5 5-7 7-9 9-11 11-13
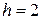
сумма частот вариант 
3 9 22 9 7
частичного интервала
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 
=1. Найти доверительный интервал для оценки неизвестного математического ожидания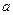 
, если выборочная средняя 
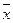=8,6, объём выборки 
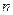=64, а надёжность оценки 
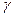=0,99.
Вариант 6
1. Вероятность выигрыша в лотерее 0,08. Некто покупает 4 билета. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Среднее число вызовов, поступающих на АТС в одну минуту, равно одному. Дискретная случайная величина Х – число вызовов за четыре минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
Среднее число вызовов, поступающих на АТС в одну минуту, равно трём. Составить закон распределения дискретной случайной величины Х – числа вызовов за две минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона). Возможные значения Х принять в интервале 0…6.
3. Вероятность появления события в каждом испытании равна 0,5. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 230 до 270, если было произведено 500 испытаний.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
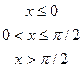Найти параметр 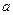, вероятность попадания случайной величины Х в интервал
(0,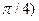 
, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,8 6мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,85 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма :
частичный интервал 3-5 5-7 7-9 9-11 11-13
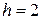
сумма частот вариант 5 10 13 12 10
частичного интервала
.
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =2. Найти доверительный интервал для оценки неизвестного математического ожидания 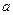, если выборочная средняя 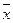=9,7, объём выборки 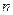=81, а надёжность оценки 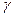=0,95.
Вариант 7
Вариант 7
1. Вероятность выигрыша в лотерее 0,09. Некто покупает 5 билетов. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Дискретная случайная величина Х – число вызовов за три минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Составить закон распределения дискретной случайной величины Х – числа вызовов за три минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона). Возможные значения Х принять в интервале 0…6.
3. Вероятность появления события в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 150 до 210, если было произведено 600 испытаний.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
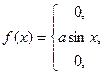
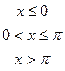Найти параметр 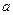, вероятность попадания случайной величины Х в интервал
(
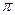/3,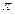 
), математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,89 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,95 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма :
частичный интервал 3-5 5-7 7-9 9-11 11-13
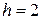
сумма частот вариант 6 12 13 11 8
частичного интервала
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =3. Найти доверительный интервал для оценки неизвестного математического ожидания 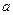, если выборочная средняя 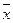=10,8, объём выборки 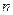=100, а надёжность оценки 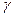=0,999.
Вариант 8
1. Вероятность выигрыша в лотерее 0,05. Некто покупает 3 билета. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
.
2. Среднее число вызовов, поступающих на АТС в одну минуту, равно полутора. Дискретная случайная величина Х – число вызовов за 3 минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики- математическое ожидание, дисперсию, среднее квадратическое отклонение.
Среднее число вызовов, поступающих на АТС в одну минуту, равно полутора.
Составить закон распределения дискретной случайной величины Х – числа вызовов за три минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона).Возможные значения Х принять в интервале 0…5.
3. Вероятность появления события в каждом испытании равна 0,25. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 140 до 210, если было произведено 700 испытаний.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
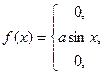
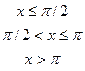Найти параметр 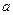, вероятность попадания случайной величины Х в интервал
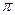( /2,2 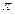/3), математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 1,2 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением
0,8 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма :
частичный интервал 3-5 5-7 7-9 9-11 11-13
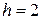
сумма частот вариант 4 7 26 8 5
частичного интервала
5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,9мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 1,2мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =4. Найти доверительный интервал для оценки неизвестного математического ожидания 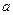, если выборочная средняя 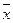=11,9, объём выборки 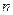=144, а надёжность оценки 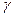=0,99.
Вариант 9
1. Вероятность выигрыша в лотерее 0,04. Некто покупает 4 билета. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Среднее число вызовов, поступающих на АТС в одну минуту, равно полутора. Дискретная случайная величина Х – число вызовов за четыре минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
Среднее число вызовов, поступающих на АТС в одну минуту, равно полутора. Составить закон распределения дискретной случайной величины Х – числа вызовов за четыре минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона).. Возможные значения Х принять в интервале 0…6.
3. Вероятность появления события в каждом испытании равна 0,2. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 140 до 220, если было произведено 900 испытаний.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
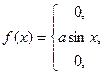
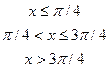Найти параметр 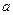, вероятность попадания случайной величины Х в интервал
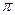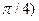( /2,3 , математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,2 мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,1 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных. 5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,2 мм. Считая случай- ную величину Х распределённой нормально со средним квадратическим отклонением
0,1 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма :
частичный интервал 3-5 5-7 7-9 9-11 11-13
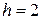
сумма частот вариант 4 7 24 9 6
частичного интервала
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =1. Найти доверительный интервал для оценки неизвестного математического ожидания 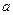, если выборочная средняя 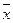=12,1, объём выборки 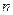=121, а надёжность оценки 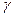=0,95.
Вариант 10
1. Вероятность выигрыша в лотерее 0,03. Некто покупает 5 билетов. Составить закон распределения дискретной случайной величины Х – числа выигрышных билетов среди купленных. Построить полигон распределения, график интегральной функции. Найти числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Среднее число вызовов, поступающих на АТС в одну минуту, равно трём с половиной. Дискретная случайная величина Х – число вызовов за полторы минуты. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
Среднее число вызовов, поступающих на АТС в одну минуту, равно трём с половиной. Составить закон распределения дискретной случайной величины Х – числа вызовов за полторы минуты. Найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение. Поток вызовов предполагается простейшим (применить формулу Пуассона).. Возможные значения Х принять в интервале 0…6.
3. Вероятность появления события в каждом испытании равна 0,5. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события заключено в пределах от 200 до 250, если было произведено 450 испытаний.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
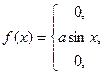
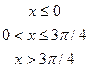Найти параметр 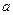, вероятность попадания случайной величины Х в интервал
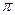( /6,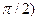 
, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,3мм. Считая случайную величину Х распределённой нормально со средним квадратическим отклонением 0,2мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра
шарика от проектного размера по абсолютной величине меньше 0,5 мм. Считая случай- ную величину Х распределённой нормально со средним квадратическим отклонением
0,3 мм, составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько в среднем будет годных шариков среди ста изготовленных.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма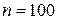 
:
частичный интервал 1-5 5-9 9-13 13-17 17-21
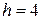
сумма частот вариант 10 20 50 12 8
частичного интервала
7. Случайная величина Х имеет нормальное распределение с известным средним квадрати ческим отклонением =2. Найти доверительный интервал для оценки неизвестного математического ожидания 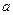, если выборочная средняя 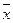=13,2, объём выборки 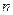=64, а надёжность оценки 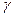=0,999.
Вариант 11
1. 1. Вероятность попадания в цель при стрельбе из орудия 0,6. Составить закон распределе-
ения дискретной случайной величины Х – числа попаданий при трёх выстрелах. Постро- ить полигон распределения, найти интегральную функцию, числовые характеристикихарактеристики - – математическое ожидание, дисперсию, среднее квадратическое отклонение.
. 2. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в
пути изделие повредится, равна 0,0002. Применяя закон распределения Пуассона, составить закон распределения дДискретнойая случайнойая величинаы Х – числао повреждённых изделий после перевозки. Применяя формулу Пуассона, Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики. Возможные значения Х принять в интервале 0…5.
3. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время Т
лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что модуль разности между числом включенных ламп и средним
числом (математическим ожиданием) включенных ламп за время Т окажется меньше трёх.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
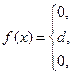
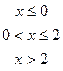Найти параметр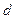 
, вероятность попадания случайной величины Х в интервал (0,3/2), математическое ожидание, дисперсию, среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
. Деталь, изготовленная автоматом, считается годной, если отклонение её контролируемого размера от проектного не превышает 10мм. Случайные отклонения
Контролируемого размера подчинены нормальному закону со средним квадратическим
отклонением 5мм и математическим ожиданием равным нулю. Составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько процентов годных деталей изготавливает автомат. 5. Деталь, изготовленная автоматом, считается годной, если отклонение её контролируемого размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера подчинены нормальному закону со средним квадратическим отклонением 5 мм и математическим ожиданием равным нулю. Составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько процентов годных деталей изготавливает автомат.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма :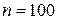
частичный интервал 2-4 4-6 6-8 8-10 10-12
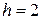
сумма частот вариант 12 22 42 14 10
частичного интервала
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =3. Найти доверительный интервал для оценки неизвестного математического ожидания 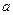, если выборочная средняя 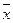=14,3, объём выборки 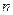=81, а надёжность оценки 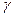=0,99.
Вариант 12
Вариант 12
3. 1. Вероятность попадания в цель при стрельбе из орудия 0,67. Составить закон распределения дискретной случайной величины Х – числа попаданий при трёхчетырёх выстрелах. Построить полигон распределения, найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
.
2. Завод отправил на базу 545000 доброкачественных изделий. Вероятность того, что в
пути изделие повредится, равна 0,0002. Дискретная случайная величина Х – число повреждённых изделий после перевозки. Применяя формулу Пуассона, Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти интегральную функцию, числовые характеристики.
Применяя закон распределения Пуассона, составить закон распределения дискретной случайной величины Х – числа повреждённых изделий после перевозки. Найти интегральную функцию, числовые характеристики. Возможные значения Х принять в интервале 0…5.
3. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время Т
лампа будет включена, равна 0,85. Пользуясь неравенством Чебышева, оценить вероятность того, что модуль разности между числом включенных ламп и средним
числом (математическим ожиданием) включенных ламп за время Т окажется меньше трёх.
4. Дана дифференциальная функция непрерывной случайной величины Х:
.
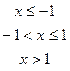Найти параметр 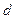, вероятность попадания случайной величины Х в интервал (-0,5;0,7), математическое ожидание, дисперсию, среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.
5. Деталь, изготовленная автоматом, считается годной, если отклонение её контролируемого размера от проектного не превышает 107 мм. Случайные отклонения
Кконтролируемого размера подчинены нормальному закону со средним квадратическим
отклонением 54 мм и математическим ожиданием равным нулю. Составить формулу дифференциальной функции (плотности вероятности) величины Х и найти, сколько процентов годных деталей изготавливает автомат.
6. Построить гистограмму относительных частот по данному распределению выборки
объёма :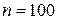
частичный интервал 2-4 4-6 6-8 8-10 10-12
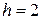
сумма частот вариант 14 24 34 16 12
частичного интервала
7. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =4. Найти доверительный интервал для оценки неизвестного математического ожидания 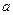, если выборочная средняя 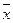=15,4, объём выборки 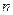=100, а надёжность оценки 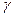=0,95.
Вариант 13
Вариант 13
4.1. Вероятность попадания в цель при стрельбе из орудия 0,68. Составить закон распределения дискретной случайной величины Х – числа попаданий при трёхпяти выстрелах. Построить полигон распределения, найти интегральную функцию, числовые характеристики – математическое ожидание, дисперсию, среднее квадратическое отклонение.
