Статические и динамические характеристики элементов и систем
Уравнения статики и динамики
Для эффективного управления технологическими процессами необхо-
димо иметь адекватное математическое описание процессов в АСР и ее эле-
ментах. Под математическим описанием (математической моделью) пони-
мают совокупность уравнений и ограничивающих условий, в количественной
форме описывающих зависимость выходных величин от входных. Эти зависи-
мости называют характеристиками. Они бывают статическими и динамически-
ми.
Динамическая характеристика (уравнение динамики) описывает изме-
нение во времени выходной величины при изменении входной величины, т.е.
переходной процесс в элементе (системе).
Статическая характеристика (уравнение статики) отражает функцио-
нальную связь между выходной и входной величинами в установившемся
режиме.
Уравнения динамики в общем виде являются дифференциальными или
интегрально-дифференциальными. Уравнения статики можно получить из
уравнений динамики, приравняв все производные по времени к нулю. И те, и
другие могут быть как линейными, так и нелинейными. Для упрощения ана-
лиза и расчетов нелинейные дифференциальные уравнения заменяют на ли-
нейные (линеаризуют) – обычно методом малых отклонений: разлагают в ряд
Тейлора вблизи интересующей точки и отбрасывают члены высшего поряд-
ка.
Статические характеристики обычно изображают в виде графиков, таб-
лиц, алгебраических уравнений, а динамические характеристики – в виде
дифференциальных уравнений или передаточных функций, временных гра-
фиков, частотных характеристик.
Дифферинцеальные уравнения элементов и систем
Преобразование лапласа,передаточная функция

где y, x – выходная и входная величины, зависящие от времени t; aп, bm – по-
стоянные коэффициенты; n ≥ m.
Уравнение, у которого правая часть равна нулю, называется однород-
ным. Если правая часть уравнения не равна нулю, то оно неоднородное. Ре-
шение однородного уравнения называется общим, или свободным.
При известных начальных условиях (функции и ее производных в на-
чальный момент времени, когда начался переходный процесс) получают ча-
стное решение уравнения. Общее решение неоднородного уравнения равно
сумме общего решения соответствующего однородного уравнения и частно-
го решения неоднородного уравнения:

Решение дифференциальных уравнений высокого порядка классиче-
ским методом довольно сложно, поэтому в теории автоматического регули-
рования используют метод интегрального преобразования Лапласа характеристическое уравнение исходного дифференциального уравнения:

Корни характеристического уравнения определяют решение однород-
ного дифференциального уравнения и потому характеризуют свободное (об-
щее) решение системы. Эти корни обращают знаменатель в нуль, а переда-
точную функцию – в бесконечность и называются полюсами передаточной
функции.
Передаточная функция связывает изображения выходной и входной
величин выражением

Применяя обратное преобразование Лапласа к изображению выходной
величины, можно найти решение исходного дифференциального уравнения,
а, значит, определить переходной процесс:

Частотные характеристики
Частотные характеристики описывают вынужденные колебания на вы-
ходе системы, вызванные гармоническими воздействиями на ее входе. При
подаче на вход элемента или системы синусоидального воздействия с ампли-
тудой Авх и частотой ω = 2π/T (где T – период колебаний)

По окончании переходного процесса на выходе устанавливаются гар-
монические колебания y t A t () sin () = вых
[ω − ϕ ω ] той же частоты, но с другой
амплитудой Aвых(ω) и сдвинутые по фазе относительно входных колебаний
на угол ϕ(ω). При изменении частоты от 0 до +∞ получают амплитудную
частотную характеристику (АЧХ) A(ω) = Aвых(ω)/Aвх и фазовую частотную
характеристику (ФЧХ) ϕ(ω) = ϕвых(ω) – ϕвх.
Для исследований и расчетов АСР применяют преобразование Фурье,
которое подобно преобразованию Лапласа, где значение p равно jω. Отно-
шение изображений по Фурье выходной и входной величин, равное

называется амплитудно-фазовой частотной характеристикой (АФЧХ).
Выделяя действительную Re(ω) и мнимую Im(ω) составляющие, можно
АФЧХ представить в алгебраической форме:

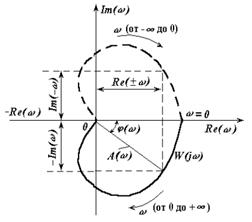
Рис 1.2 Амплитудно частотная характеристика
Зависимость Re(ω) называют действительной частотной характеристикой,
а зависимость Im(ω) − мнимой частотной характеристикой. АФЧХ можно построить на комплексной плоскости при изменении частоты только от 0 до +∞,
так как она симметрична относительно действительной оси (рис. 1.2). АФЧХ
можно представить в виде радиуса-вектора на комплексной плоскости и за-
писать в экспоненциальной форме:

Значения модуля и аргумента вектора определяют по формула


Используя приведенные характеристики можно проводить исследова-
ния АСР. Ряд характеристик удобно получать по экспериментальным дан-
ным, не зная точного математического описания элементов и систем.






