Из одной вершины в другую.
Пусть G – некий ориентированный нагруженный граф. Пусть y и z – какие-то вершины графа G. Требуется найти путь наименьшей длины из y в z.
Замечание. Алгоритм решения данной задачи называется алгоритмом в честь математика Е. Дийкстра, опубликовавший этот алгоритм в 1959 году.
Суть алгоритма заключается в следующем: на каждом шаге алгоритма каждая вершина x графа G имеет метку s(x), которая может быть либо временной меткой, либо постоянной (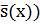
. Значение постоянной метки 
(на каждом шаге алгоритма) равно длин кратчайшего пути из начальной вершины в конечную. Значение временной метки s(x) (на каждом шаге алгоритма) есть длина кратчайшего (y,x)-пути, проходящего только через вершины, имеющие к данному моменты постоянные метки . Кроме временной метки каждой вершине графа (кроме начальной вершины y) присваивается также метка g(x). Ее значение на каждом шаге равно номеру вершины графа, предшествующей вершине x в (y,x)-пути, имеющем наименьшую длину среду всех (y,x)-путей, проходящих через вершины, получившие к данному моменту постоянные метки. В конце алгоритма метки g(x) позволяет выписать кратчайший (y,z)-путь в виде следующей последовательности: (y,…,q(q(z)),q(z),z).
Алгоритм поиска кратчайшего (y,z)-пути
В нагруженном графе.
Шаг 1. Положим 
:=0 и будем считать данную метку постоянной. Всем остальным вершинам графа присваиваем временные метки, равные бесконечности, и индексу p:=y (присваиваем имя начальной вершины).
Шаг 2. Сформируем множество L(p) ={ a ϵ XG: (p, a) ϵ PG }. Для каждой вершины из множества L(p) проверяем выполнение неравенства s(a) > 
+ l (p,a).
Если данное неравенство выполняется, то вершине a присваиваем метку s(a), равную следующему выражению s(a):= + l (p,a), и одновременно метке q(a):=p. Если же неравенство не выполняется, то значение меток s(a) и q(a) не меняются.
Шаг 3. Сформируем множество X´, элементами которого являются все вершины графа G, имеющие к данному моменту временные метки s(x). Среди элементов множества X´ выбираем такой элемент x*, у которого временная метка s(x*) имеет наименьшее значение среди меток s(x), где x ϵ X´. Метку s(x*) считаем постоянной.
Шаг 4. Индексу p:=x*. Если p=z, то переходим к шагу 5. В противном случае переходим в шагу 2 алгоритма.
Шаг 5. По известным меткам q(x) выписываем кратчайший (y,z))-путь:
μ*(y,z) = (y,…,q(q(z)),q(z),z).
Решение:
Сформируем матрицу достижимости T(G).
T(G) =
Будем считать вершину 1 стартовой в алгоритме поиска кратчайших путей в графе G.
Изобразим ориентированный граф G с величинами нагрузок дуг:
Шаг 1. Метки s вершины 1 присваиваем значение 0 и считаем эту метку постоянной. Остальным вершинам присваиваем временные метки s, равные ∞. p:=1 (номер начальной вершины).
Шаг 2. Формируем множество L(1)={3,6,9}. Для каждой вершины L(1) проверяем выполнение неравенства s(x)> 
(1)+l(1,x):
s(3)> (1)+l(1,3)- верно,
s(6)> (1)+l(1,6)- верно,
s(9)> (1)+l(1,9)- верно.
Таким образом, каждой вершине множества L(1) присваиваем новые метки s(x):= (1)+l(1,x); q(x)=1, получаем
s(3):=6, q(3)=1;
s(6):=17, q(6)=1;
s(9):=21, q(9)=1.
Шаг 3. Формируем множество x'={2,3,4,5,6,7,8,9,10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (3)=6, x*=3, считаем ее постоянной, p:=3.
Шаг 4. Формируем множество L(3)=Ø. Следовательно, на данном этапе метки не меняются.
Шаг 5. Формируем множество x'={2,4,5,6,7,8,9,10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (6)=17, x*=6, считаем ее постоянной, p:=6.
Шаг 6. Формируем множество L(6)={7,9}. Для каждой вершины L(6) проверяем выполнение неравенства s(x)> (6)+l(6,x):
s(7)> (6)+l(6,7)- верно,
s(9)> (6)+l(6,9)- неверно.
Таким образом, вершине 7 множества L(6) присваиваем новую метку s(x):= (6)+l(6,x); q(x)=6, получаем
s(7):=34, q(7)=6;
a вершине 9 на данном этапе алгоритма метки не меняем.
Шаг 7. Формируем множество x'={2,4,5,7,8,9,10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (9)=21, x*=9, считаем ее постоянной, p:=9.
Шаг 8. Формируем множество L(9)=Ø. Следовательно, на данном этапе метки не меняются.
Шаг 9. Формируем множество x'={2,4,5,7,8, 10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (7)=34, x*=7, считаем ее постоянной, p:=7.
Шаг 10. Формируем множество L(7)={4,8}. Для каждой вершины L(7) проверяем выполнение неравенства s(x)> (7)+l(7,x):
s(4)> (7)+l(7,4)- верно,
s(8)> (7)+l(7,8)- верно.
Таким образом, каждой вершине множества L(7) присваиваем новые метки s(x):= (7)+l(7,x); q(x)=7, получаем
s(4):=46, q(3)=7;
s(8):=41, q(6)=7.
Шаг 11. Формируем множество x'={2,4,5, 8, 10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (8)=41, x*=8, считаем ее постоянной, p:=8.
Шаг 12. Формируем множество L(8)={2}. Для каждой вершины L(8) проверяем выполнение неравенства s(x)> (8)+l(8,x):
s(2)> (8)+l(8,2)- верно.
Таким образом, каждой вершине множества L(8) присваиваем новые метки s(x):= (8)+l(8,x); q(x)=8, получаем
s(2):=46, q(2)=8.
Шаг 13. Формируем множество x'={2,4,5,10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (2)=46, x*=2, считаем ее постоянной, p:=2.
Шаг 14. Формируем множество L(2)={4}. Для каждой вершины L(2) проверяем выполнение неравенства s(x)> (2)+l(2,x):
s(4)> (2)+l(2,4)- неверно.
Таким образом, на данной этапе алгоритма вершине 2 метки не меняем.
Шаг 15. Формируем множество x'={4,5,10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (4)=46, x*=4, считаем ее постоянной, p:=4.
Шаг 16. Формируем множество L(4)={10}. Для каждой вершины L(4) проверяем выполнение неравенства s(x)> (4)+l(4,x):
s(10)> (4)+l(4,10)- верно.
Таким образом, каждой вершине множества L(4) присваиваем новые метки s(x):= (4)+l(4,x); q(x)=4, получаем
s(10):=61, q(2)=4.
Шаг 17. Формируем множество x'={5,10}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (10)=61, x*=10, считаем ее постоянной, p:=10.
Шаг 18. Формируем множество L(10)=Ø. Следовательно, на данном этапе метки не меняются.
Шаг 19. Формируем множество x'={5}. Выбираем вершину x* из множества x' с наименьшей меткой s, получаем (5)=∞, x*=5, считаем ее постоянной, p:=5.
Так как все вершины получили постоянные метки, алгоритм закончен.
Выпишем кратчайшие пути от вершины 1 до всех вершин ориентированного графа G, достижимых из вершины 1, и найдем их длины (величина, равная сумме нагрузок всех дуг пути μ*):
μ*(1,2)=(1,6,7,8,2);
l (μ*(1,2))=46;
μ*(1,3)=(1,3);
l (μ*(1,3))=6;
μ*(1,4)=(1,6,7,4);
l (μ*(1,4))=46;
μ*(1,6)=(1,6);
l (μ*(1,6))=17;
μ*(1,7)=(1,6,7);
l (μ*(1,7))=34;
μ*(1,8)=(1,6,7,8);
l (μ*(1,8))=41;
μ*(1,9)=(1,9);
l (μ*(1,9))=21;
μ*(1,10)=(1,6,7,4,10);
l (μ*(1,10))=61.
