Алгоритм выделения компонент
Шаг 1. Полагаем p=1, D1(G) = D(G).
Шаг 2. Включаем во множество вершин 
очередной (р -й) компоненты сильной связности Hp графа G вершины, соответствующие единицам первой строки матрицы Dр(G). В качестве матрицы смежности графа Hp – A(Hp) берем подматрицу матрицы A(G), элементы которой находятся на пересечении строк и столбцов, соответствующих вершинам из .
Шаг 3. Вычеркиваем из Dр(G) строки и столбцы, соответствующие вершинам . Если в результате не остаётся ни одной строки (и соответственно ни одного столбца), то р - количество компонент H1, H2,…, Hp сильной связности графа G, соответственно A(H1), A(H2),…, A(Hp) – их матрицы смежности. В противном случае обозначим оставшуюся после вычеркивания из Dр(G) соответствующих строк и столбцов матрицу через Dр+1 (G), положим р=р+1 (увеличим значение индекса р на единицу) и перейдем к шагу 2.
Решение:
Выпишем ранее сформированную матрицу смежности ориентированного графа G.
A(G) =
Построим матрицу сильной связности графа G.
D(G) =
Так как матрица D(G) полностью состоит из единиц, то единственной компонентой связности графа G будет сам ориентированный граф G.
H1
Задание 8.
Найти компоненты связности неориентированного графа G´.
Определение. Компонентами связности неориентированного графа называются все его связные подграфы, не являющиеся собственными подграфами никакого другого связного подграфа графа G´.
Замечание. Неориентированные графы обладают следующим важным свойством: каждый неориентированный граф можно представить в виде объединения его компонент связности. Разложение неориентированного графа на его компоненты связности единственно и однозначно.
Определение. Пусть дан граф G´ - неориентированный. Матрицей связности графа G´ называется матрица D(G´) [n x n], где n – мощность множества вершин, с элементами dij 
, которые определяются следующим условием:
dij = 
Замечание. Отметим, что, после внесения соответствующих изменений в обозначения и терминологию рассмотренного ранее алгоритма выделения компонент сильной связности ориентированного графа G, его можно применять и для нахождения компонент связности неориентированного графа G´.
Решение:
Выпишем ранее сформированную матрицу смежности неориентированного графа G´.
A(G´) =
Построим матрицу связности неориентированного графа D(G´).
D(G´) =
Так как матрица D(G´) полностью состоит из единиц, то единственной компонентой связности графа G´ будет сам неориентированный граф G´.
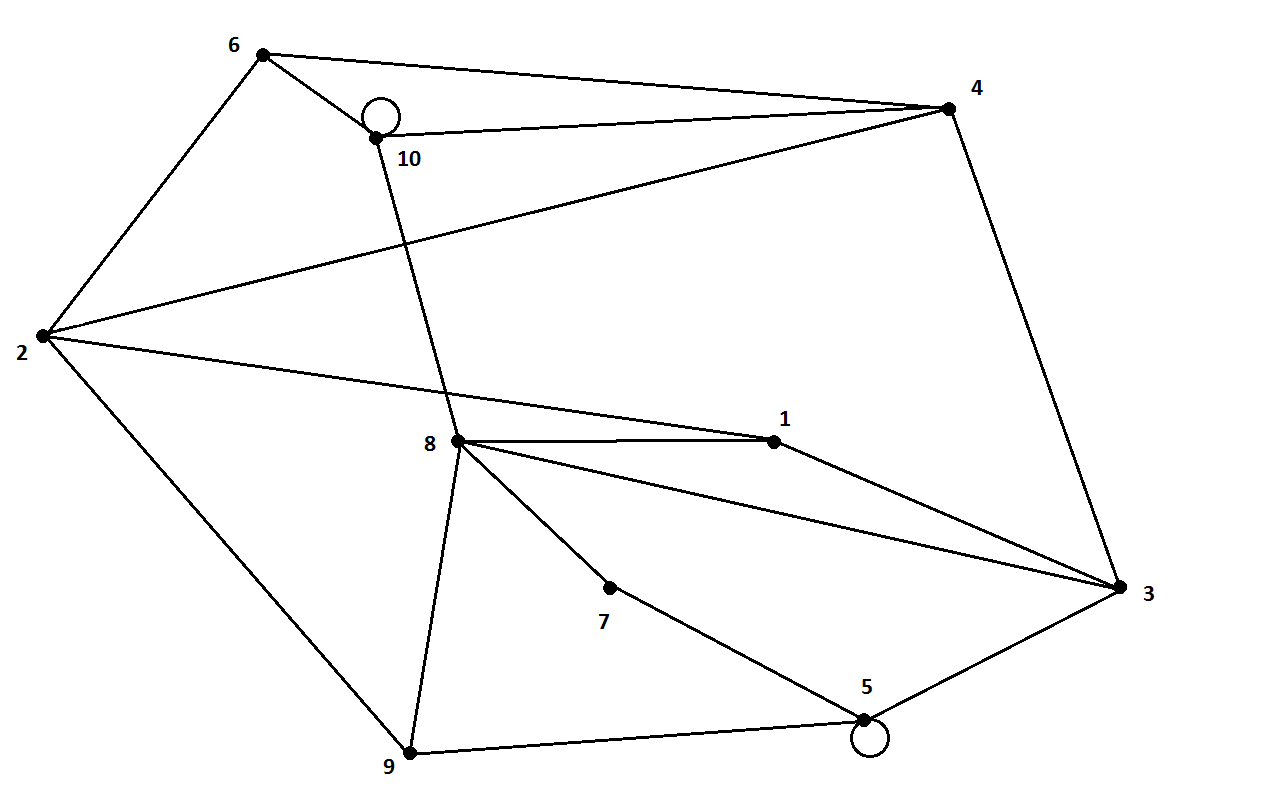
H1
Задание 9.
Перечислить все пути в ориентированном графе G, состоящие из четырех дуг.
Определение. Пусть задан ориентированный граф G = (XG, PG) и пусть xi 1, xin ϵ XG. Kортеж вида (xi1, xi2,…,xin-1,xin) называется путем из вершины xi1 в вершину xin графа G, если для любого k от 1 до n-1 двойка (xik, xik+1)ϵ PG .
