Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а1, а2, …, аn не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико.
26) Теорема Бернулли. Если в каждом из независимых испытаний вероятность появления события постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Теорема Чебышева в 25.
27) Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений случайной величины, является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью. Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это всегда результат ограниченного ряда наблюдений.
Вариационный ряд - последовательность x(1), x(2), x(3),..., x(k),..., x(n), полученная в результате расположения в порядке неубывания исходной последовательности независимых одинаково распределённых случайных величин x1, x2, x3,..., xn.
Полиго́н часто́т (в математической статистике) — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
Гистогра́мма в математической статистике - это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него.
28) ЭМПИРИЧЕСКАЯ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ
(frequency distribution) Функция, описывающая распределение случайных значений переменной. Если переменная х принимает значения на непрерывном отрезке и имеет минимальное значение а и максимальное значение b, эмпирическая плотность распределения обозначается как f(x). Интеграл функции f(x) на отрезке от а до b, ſba f(x)dx должен быть равен 1. Кумулятивная плотность распределения F(c) показывает долю значений, равных или меньших чем с; F(c) = ſca vf(x)dx < 1. В тех случаях, когда переменная может принимать только одно из множества дискретных значений с минимумом ν1 и максимумом νn, плотность распределения записывается в виде f(νi) = fi, где Σi fi (νi)=1
30) 1.1.Генеральная средняя.
Пусть изучается генеральная совокупность относительно количественного признака Х.
Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.
Если все значения признака различны, то

Если значения признака имеют частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то
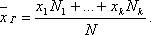
1.2.Выборочная средняя.
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.
Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.
31) 1.3. Генеральная дисперсия.
Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.
Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения.
Если все значения признака генеральной совокупности объема N различны, то

Если же значения признака имеют соответственно частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то

Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.
Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

1.4.Выборочная дисперсия.
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику- выборочную дисперсию.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

32) В качестве описательных характеристик вариационного ряда используется медиана, мода и размах.
Размахом вариации называется число R = xmax – xmin, где
Xmax - наибольший из вариант,
Xmin - наименьший из вариант.
Модой М0* вариационного ряда называется вариант, имеющий наибольшую частоту.
Медианой Ме* вариационного ряда называется значение признака, приходящегося на середину ряда.
Если объем выборки n – четное число, то 
Если объем выборки нечетное число, то 
33) Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d, то чем меньше d, тем оценка точнее.
34) Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100p%[примечание 1], порождённым выборкой (x1,…,xn), называется интервал с границами (x1,…,xn) и (x1,…,xn), которые являются реализациями случайных величин L(X1,…,Xn) и U(X1,…,Xn), таких, что
. 
Граничные точки доверительного интервала и называются доверительными пределами.
Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.
Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.
40) Любую задачу линейного программирования можно свести к стандартной форме, так
называемой «основной задаче линейного программирования» (ОЗЛП), которая
формируется так: найти неотрицательные значения переменные x1
, x2,., xn, которые удовлетворяли бы
условиям – равенствам:
a11 x1 + a12 x2 +. +a1n xn = b1,
a21 x1 + a22 x2 +. +a2n xn = b2,
..............
am1 x1 +am2 x2 +. +amn xn = bm.
и обращали бы в максимум линейную функцию этих переменных: 
42) Множество и элемент множества относятся к числу первичных понятий, для которых не существует определений в строгом смысле слова. Поэтому обычно говорят о множестве как о наборе предметов (элементов множества), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.
Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.
Пустое множество () не содержит ни одного элемента, например, множество крылатых слонов, множество корней уравнения sin x = 2 и т.д.
Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.
Счётное множество – множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке) или бесконечным (множество целых чисел, его элементы можно пронумеровать следующим образом:
элементы множества: …, –5, – 4, –3, –2, –1, 0, 1, 2, 3, 4, 5, …
номера элементов:... 11 9 7 5 3 1 2 4 6 8 10...).
Несчётное множество – множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным (продумайте, почему?).
Выпуклое множество – множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружность не является выпуклым множеством.
Способы задания множеств. Множество может быть задано следующим образом:
– перечислением всех его элементов по их названиям (так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);
– заданием общей характеристики (общих свойств) элементов данного множества (например, множество рациональных чисел, собаки, семейство кошачих и т.д.);
– формальным законом построения элементов множества (например, формула общего члена числовой последовательности, Периодическая система элементов Менделеева и т.д.).
43) 
44) 






