Определение законов сопротивления и значения
Критического числа Рейнольдса при ламинарном
И турбулентном режимах течения жидкости
Цель работы и содержание работы
Исследовать режимы течения жидкости в трубопроводах, определить критическое число Рейнольдса и характеристики сопротивления движению жидкости по трубопроводу.
2.2 Краткие теоретические сведения
Виды режимов течения
В реальном потоке жидкости, как показывают многочисленные опыты, возможны разные течения жидкости.
1. Ламинарное (слоистое) течение, в котором частицы жидкости двигаются в своих слоях не перемешиваясь. При этом сами частицы внутри слоя имеет вращательное движение (рисунок 2.1) за счет градиента скоростей 
.
Рисунок 2.1
При увеличении скорости течения жидкости – скорость V увеличивается, градиент скорости 
, соответственно. Увеличивается вращательное движение частиц, при этом скорость более удаленного от стенки слоя еще более увеличивается (рисунок 2.2), a скорость пристеночных слоев еще более уменьшается.
Рисунок 2.2
Соответственно в пристеночных слоях увеличивается гидромеханическое давление (по уравнению Бернулли). Под действием разности давления вращающаяся частица перемешается в толщу ядра (рисунок 2.3), образуя второй режим течения жидкости – турбулентное течение.
Рисунок 2.3
2. Турбулентное течение жидкости сопровождается интенсивным перемешиванием жидкости и пульсацией скоростей и давлений (рисунок 2.4).
Рисунок 2.4
Немецкий ученый О. Рейнольдс в 1883 г. доказал, что переход от ламинарного течения жидкости к турбулентному зависит от вязкости жидкости, ее скорости и характерного размера (диаметра) трубы.
Критическая скорость, при которой ламинарное течение переходит в турбулентное, равна:
,
где K – универсальный коэффициент пропорциональности (он одинаков для всех жидкостей и диаметров труб); d – диаметр трубопровода.
Этот безразмерный коэффициент был назван критическим числом Рейнольдса:
. (2.1)
Как показывают опыты, для жидкостей 
. Очевидно, число Re может служить критерием, позволяющих судить о режиме течения жидкости в трубах, так
при 
течение ламинарное,
при 
течение турбулентное.
На практике ламинарное течение наблюдается при течении вязких жидкостей (в гидро- и маслосистемах самолета). Турбулентное течение наблюдается в водопроводе, в топливных (керосин, бензин, спирт) системах.
В гидравлических системах наблюдается еще один вид течения жидкости – кавитационный режим течения. Это движение жидкости, связанное с изменением ее агрегатного состояния (превращение в газ, выделение растворенного воздуха и газов). Это явление наблюдается тогда, когда местное статическое давление снижается до давления упругости насыщенных паров жидкости, то есть при 
(рисунок 2.5)
Рисунок 2.5
В этом случае в данной месте потока начинается интенсивное парообразование и выделение воздуха и газов. В потоке образуются газовые полости («кавитас» – полость). Такое течение жидкости называется кавитационным. Кавитация – явление опасное, ибо, во-первых, ведет к резкому уменьшению расхода жидкости (а следовательно, и к возможному выключению двигателя при кавитации в топливной системе), и, во-вторых, пузырьки газа, воздействуя на лопатки насосов, разрушают их.
В топливных системах борются с кавитацией путем повышения давления в баках или системе с помощью подкачивающих насосов и системы наддува баков. Это явление необходимо учитывать при проектировании и конструировании гидросистем летательных аппаратов (особенно топливной). Дело в том, что по ряду причин эти системы соединены с атмосферой (система суфлирования). С подъемом на высоту давление над поверхностью емкостей систем уменьшается, следовательно, уменьшается статическое давление в трубопроводах. В сочетании с потерями давления на местных сопротивлениях и уменьшением статического давления при больших скоростях течения в трубопроводах возникает опасность появления кавитационных давлений.
Основы теория ламинарного течения жидкости
В трубах
Ламинарное течение является строго упорядоченным слоистым течением и подчиняется закону трения Ньютона:
(2.2)
Рассмотрим установившееся ламинарное течение жидкости в круглой прямой трубе (рисунок 2.6), расположенной горизонтально (
). Поскольку труба цилиндрическая, то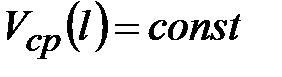 
и в этом случае уравнение Бернулли примет вид:
, (2.3)
Отсюда
. (2.4)
Выделим в жидкости (рисунок 2.6) объем жидкости радиусом r и длиной l. Очевидно, постоянство скорости будет обеспечено, если сумма сил давления и трения, действующая на выделенный объем, будет равна нулю, то есть
,
откуда
. (2.5)
Касательные напряжения в поперечном сечении трубы изменяются по линейному закону пропорционально радиусу (рисунок 2.6).
Рисунок 2.6
Приравнивая (2.4) и (2.5), получим:
,
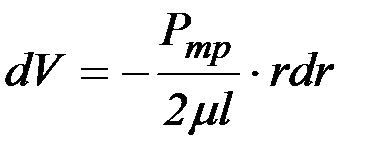или, интегрируя от r = 0 до r = r0, получаем закон распределения скоростей по сечению круглой трубы:
. (2.6)
Расход жидкости определяется как dQ = VdS. Подставляя в последнее выражение (2.6) и учитывая, что dS = 2prdr, после интегрирования получаем:
. (2.7)
Следовательно, расход жидкости при ламинарном течении пропорционален радиусу трубы в четвертой степени.
. (2.8)
Сравнивая (2.6) и (2.8), получаем, что
. (2.9)
Для определения потерь напора на трение – 
, определим 
из (2.7):
. (2.10)
Следовательно,
(2.11)
или, заменяя m через nr и g через qr, получим
(2.12)
Таким образом, при ламинарном течении в круглой трубе потери налога за трение пропорциональны расходу жидкости и вязкости, и обратно пропорциональны диаметру трубы в четвертой степени. Чем меньше диаметр трубы, тем больше потери напора на трение.
Ранее мы условилась, что потери на гидросопротивления всегда пропорциональны квадрату скорости жидкости. Для получения такой зависимости соответственно преобразуем выражение (2.12), учитывая, что
, а 
.
После соответствующих преобразований получим:
, (2.13)
или
, (2.14)
где
(2.15)
– коэффициент сопротивления трения при ламинарном течении.
Осталось определять коэффициент 
, учитывающий неравномерность распределения скоростей в сечении трубы для уравнения Бернулли.
В учебнике Б.Е. Некрасова показано, что
. (2.16)
Поскольку 
, то dS=2prdr, подставляя в (2.16) и (2.8), после сокращения получим:
. (2.17)
В заключение следует отметить, что если жидкость из резервуара входит в трубу, постоянного диаметра и движется в ней ламинарным потоком, то формирование параболического профиля скоростей осуществляется постепенно, на некотором начальном участке 
(рисунок 2.7).
Рисунок 2.7
Полученные выше соотношения справедливы лишь на участке, где 
. Определение потерь напора на участке осуществляется по тем не формулам, но с поправочным коэффициентом 
:
, (2.18)
где 
определяется по графику (рисунок 2.8).
Рисунок 2.8
Следует отметить, что длина начального участка относительно невелика по сравнению с длиной трубопровода, и поэтому в расчетах иногда считают, что характеристика течения та же, что и после переходного участка, то есть считают 
.
