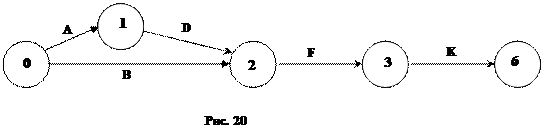Рассматривается строительство животноводческого комплекса. Строительство комплекса предполагает выполнение работ, список которых задан: A, B, C, D, E, F, G, H, K, L, M, N. Последовательность выполнения работ определяется сетевым графиком (рис.6). Для каждой работы задано время её выполнения (табл. 6).
Время выполнения работ Таблица 6
| № работы | Работа | Время выполнения работы дни |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
| G | ||
| H | ||
| K | ||
| L | ||
| M | ||
| N |
Определить: 1) Временные характеристики событий, критическое время выполнения всех работ, а также критические события; 2) Полный резерв времени для каждой работы, критические работы; 3) Построить сетевой график критических работ и путей.

Решение. 1) Определим временные характеристики событий: раннее время наступления события 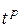 , позднее время наступления события
, позднее время наступления события  и резерв времени события Δ =
и резерв времени события Δ =  –
– 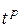 .
.
Сначала найдём значения раннего времени наступления каждого события. Первым определим раннее время начального события (событие 0). Полагаем, что раннее время начального события равно 0:  .
.  Найдём раннее время 1 события
Найдём раннее время 1 события 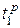 . Рассмотрим работы, входящие в событие 1
. Рассмотрим работы, входящие в событие 1
(рис. 7). Это работа А, которая начинается событием 0. Так как в событие 1 входит одна работа, то  =0+7=7 дней.
=0+7=7 дней.
Определим раннее время 2 события  . Рассмотрим работы, входящие в событие 2 (рис. 8). Это работы B, которая начинается событием 0, и работа D, которая начинается событием 1. Для каждой из работ найдём сумму раннего времени начала работы и её продолжительности. Раннее время 2 события
. Рассмотрим работы, входящие в событие 2 (рис. 8). Это работы B, которая начинается событием 0, и работа D, которая начинается событием 1. Для каждой из работ найдём сумму раннего времени начала работы и её продолжительности. Раннее время 2 события  равно максимуму этих сумм:
равно максимуму этих сумм:  = max{0+11;7+4}=11 дней.
= max{0+11;7+4}=11 дней.

Вычислим раннее время 3 события  . Рассмотрим работы, входящие в событие 3 (рис. 9). Это работы С, которая начинается событием 1, и F, которая начинается событием 2. Аналогично времени
. Рассмотрим работы, входящие в событие 3 (рис. 9). Это работы С, которая начинается событием 1, и F, которая начинается событием 2. Аналогично времени  определяем время
определяем время 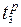 :
:  = max{7+8;11+6}=17 дней.
= max{7+8;11+6}=17 дней.
Найдём раннее время 4 события 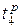 . Рассмотрим работы, входящие в событие 4 (рис. 10). Это работы Е и G. Тогда раннее время 4 события
. Рассмотрим работы, входящие в событие 4 (рис. 10). Это работы Е и G. Тогда раннее время 4 события 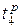 :
:

 = max{7+15;17+9}=26 дней.
= max{7+15;17+9}=26 дней.
Определим раннее время 5 события  . Входящие работы H и L (рис. 11). Тогда
. Входящие работы H и L (рис. 11). Тогда 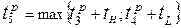 = max{17+13;26+3}=30 дней.
= max{17+13;26+3}=30 дней.
Вычислим время  . Входящие работы K, M и N (рис. 12).
. Входящие работы K, M и N (рис. 12). 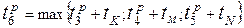 = max{17+16;26+5;30+2}=33 дня.
= max{17+16;26+5;30+2}=33 дня.
Определяем критическое время:  =
=  =33 дня.
=33 дня.

Найдём значения позднего времени наступления каждого события.
Сначала найдём позднее время конечного события (событие 6). Полагаем, что позднее время конечного события равно:  .
.
Найдём позднее время 5 события  . Рассмотрим работы, выходящие из события 5 (рис. 13). Это работа N, которая заканчивается событием 6. Так как выходящая из события 5 работа одна, то позднее время 5 события равно:
. Рассмотрим работы, выходящие из события 5 (рис. 13). Это работа N, которая заканчивается событием 6. Так как выходящая из события 5 работа одна, то позднее время 5 события равно:  33–2=31.
33–2=31.
Определим позднее время 4 события 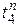 . Рассмотрим работы, выходящие из события 4 (рис. 14). Это работы L, которая заканчивается событием 5, и M, которая заканчивается событием 6. Для каждой из работ найдём разность позднего времени окончания работы и его продолжительности. Позднее время события 4,
. Рассмотрим работы, выходящие из события 4 (рис. 14). Это работы L, которая заканчивается событием 5, и M, которая заканчивается событием 6. Для каждой из работ найдём разность позднего времени окончания работы и его продолжительности. Позднее время события 4, 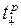 равно минимуму этих разностей:
равно минимуму этих разностей:  = min{31–3;33–5}=28.
= min{31–3;33–5}=28.
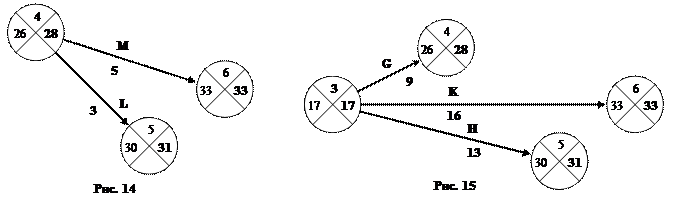
Вычислим позднее время 3 события  . Рассмотрим работы, выходящие из события 3 (рис. 15). Это работа G, которая заканчивается событием 4, работа H, которая заканчивается событием 5, и работа K, которая заканчивается событием 6. Аналогично позднему времени 4 события определяем позднее время 3 события
. Рассмотрим работы, выходящие из события 3 (рис. 15). Это работа G, которая заканчивается событием 4, работа H, которая заканчивается событием 5, и работа K, которая заканчивается событием 6. Аналогично позднему времени 4 события определяем позднее время 3 события  :
:  = min{28–9;31–13;33–16}=17.
= min{28–9;31–13;33–16}=17.
Найдём позднее время 2 события 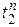 . Рассмотрим работы, выходящие из события 2
. Рассмотрим работы, выходящие из события 2
(рис. 16). Это работа F, которая заканчивается событием 3. Тогда позднее время 2 события равно:  33–2=31.
33–2=31.
Определим позднее время 1 события  . Выходящие из события 1 работы – это работы D, C и E (рис. 17). Позднее время события 1 равно:
. Выходящие из события 1 работы – это работы D, C и E (рис. 17). Позднее время события 1 равно:  = min{11–4;17–8;28–15}=7.
= min{11–4;17–8;28–15}=7.

 Вычислим позднее время начального события
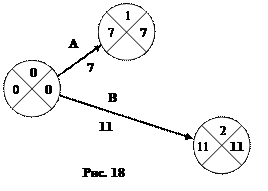
Вычислим позднее время начального события  . Входящие в событие 0 работы – это работы K, M и N (рис. 18). Находим позднее время начального события:
. Входящие в событие 0 работы – это работы K, M и N (рис. 18). Находим позднее время начального события:  =min{7–7;11–11}=0.
=min{7–7;11–11}=0.
В качестве промежуточной проверки сверяется значение  . Оно должно равняться 0. Вычислим резервы времени событий, также определим критические события (резервы времени которых равны 0). Резерв времени события равен:
. Оно должно равняться 0. Вычислим резервы времени событий, также определим критические события (резервы времени которых равны 0). Резерв времени события равен:  ; а также критические события:
; а также критические события:
 = 0 – 0 = 0, 0 событие критическое;
= 0 – 0 = 0, 0 событие критическое;
 = 7 – 7 = 0, 1 событие критическое;
= 7 – 7 = 0, 1 событие критическое;
 |
 = 11 – 11 = 0, 2 событие не критическое;
= 11 – 11 = 0, 2 событие не критическое;  = 17 – 17 = 0, 3 событие критическое;
= 17 – 17 = 0, 3 событие критическое;  = 28 – 26 = 2, 4 событие некритическое;
= 28 – 26 = 2, 4 событие некритическое;  = 31 – 30 = 1, 5 событие некритическое;
= 31 – 30 = 1, 5 событие некритическое;  = 33 – 33 = 0, 6 событие критическое.
= 33 – 33 = 0, 6 событие критическое.
Резервы времени каждого события отметим на сетевом графике (рис. 19).
2) Полный резерв времени работы  равен разности позднего времени её окончания и раннего времени её начала минус продолжительность работы:
равен разности позднего времени её окончания и раннего времени её начала минус продолжительность работы:  , где
, где  – позднее время окончания работы,
– позднее время окончания работы,  – раннее время её начала,
– раннее время её начала,  – продолжительность работы. Вычисления удобнее производить с помощью таблицы (табл. 7).
– продолжительность работы. Вычисления удобнее производить с помощью таблицы (табл. 7).
Полный резерв времени можно вычислять последовательно, по списку работ, а можно порядок вычислений осуществлять по номеру начала работы. Для работ с одним началом порядок очерёдности определяется по номеру окончания работы. Например, сначала вычисляется полный резерв времени для работ 0 – 1, 0 – 2, потом 1 – 2, 1 – 3, 1 – 4, 1 – 5, потом 2 – 3, 2 – 5, 3 – 4, 3 – 5, 3 – 6, 4 – 5, 4 – 6.
Временные характеристики работ Таблица 7
| Начало и окончание работы | Работа | Раннее время начала | Позднее время окончания | Время работы | Полный резерв времени работы |
| 0-1 | A | ||||
| 0-2 | B | ||||
| 1-2 | D | ||||
| 1-3 | C | ||||
| 1-4 | E | ||||
| 2-3 | F | ||||
| 3-4 | G | ||||
| 3-5 | H | ||||
| 3-6 | K | ||||
| 4-5 | L | ||||
| 4-6 | M | ||||
| 5-6 | N |
Примечание: шрифтом выделены критические работы.
3) Строим сетевой график критических работ: сначала располагаем на графике критические события: 0, 1, 2, 3, 6; а потом их соединяем критическими работами: 0–1, 0–2, 1–2, 2–3, 3–6 (рис.20).