Методические указания к заданию № 1

Контрольная работа № 2

Условия заданий

Задание №1

В хозяйстве необходимо за время уборки при заготовке силоса перевезти 4000 т зелёной массы с пяти поля (табл. 1) к четырём силосным траншеям (табл.2).

Количество зелёной массы, перевозимой с полей, т Таблица 1

Предпоследняя цифра шифра	Поле
1-е	2-е	3-е	4-е	5-е

 

Вместимость силосных траншей зелёной массы, т Таблица 2

Последняя цифра шифра	Силосная траншея
1-я	2-я	3-я	4-я

Оплата за тонну зелёной массы, перевозимую с полей к силосным траншеям, приведена в табл. 3.

 

Оплата перевозки тонны зелённой массы от полей до силосных траншей, руб. Таблица 3

Поля	Приёмные пункты
1-ый	2-ой	3-ий	4-ый
1-е
2-е
3-е
4-е
5-е

Составить такой план перевозок, чтобы транспортные затраты на перевозку зелёной массы с полей до силосных траншей были минимальными. Опорный план найти методом наименьшего элемента. Оптимальный план найти методом потенциалов.

 

Задание №2

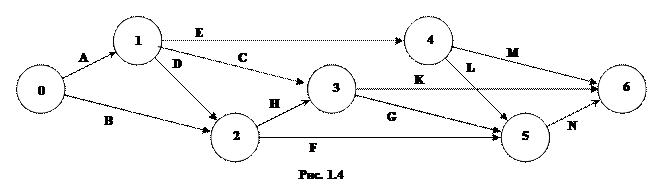
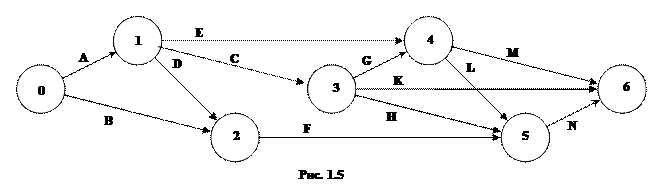
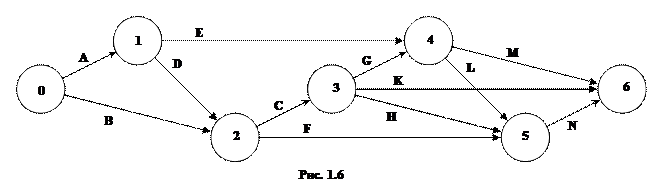
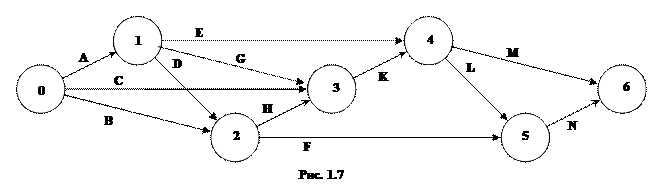
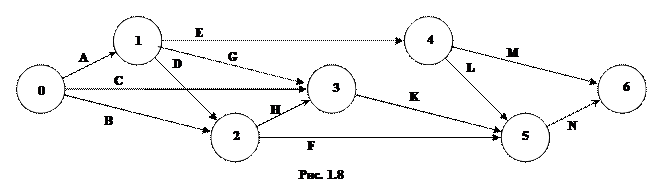
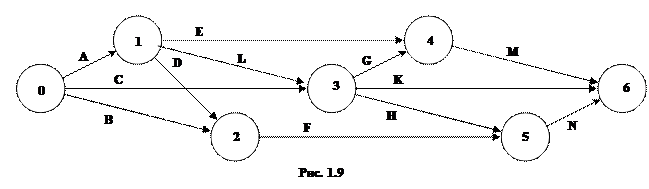
Рассматривается строительство животноводческого комплекса. Строительство комплекса предполагает выполнение работ, список которых задан: A, B, C, D, E, F, G, H, K, L, M, N. Последовательность выполнения работ определяется сетевым графиком (предпоследняя цифра шифра определяет номер рисунка). Для каждой работы задано время её выполнения (табл. 4).

Определить: 1) Временные характеристики событий, критическое время выполнения всех работ, а также критические события; 2) Полный резерв времени для каждой работы, критические работы; 3) Построить сетевой график критических работ и путей.

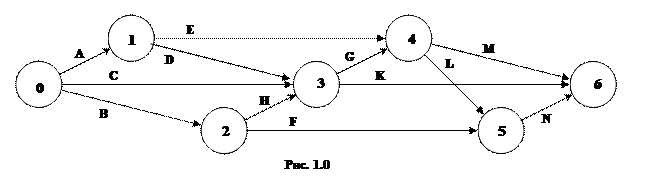
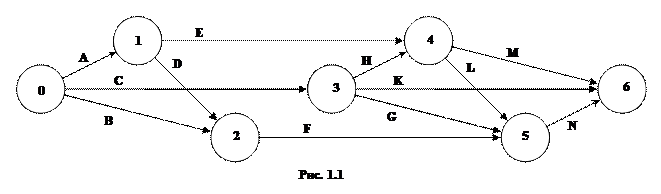
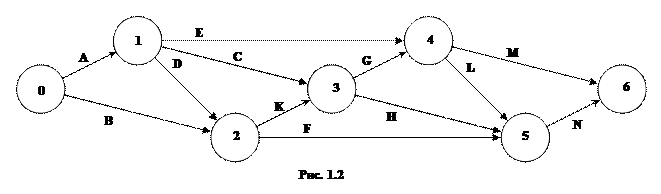
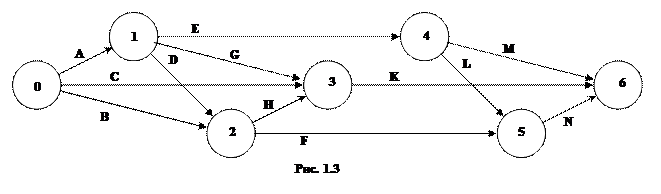
Время выполнения работ Таблица 4

№ работы	Работа	Время выполнения работы, дни (последняя цифра шифра)
	A
	B
	C
	D
	E
	F
	G
	H
	K
	L
	M
	N

 

Методические указания по выполнению контрольной работы № 2

Методические указания к заданию № 1.

В хозяйстве необходимо за время уборки при заготовке силоса перевезти 3600 т зелёной массы с пяти поля к четырём силосным траншеям. Зелёная масса каждого поля равна: А₁ =400, А₂ =500, А₃ =700, А₄ =900, А₅ =1100 т; вместимости силосных траншей равны: В₁ =1200, В₂ = 600, В₃ =800, В₄ =1000 т. Оплата за тонну зелёной массы, перевозимую с полей к силосным траншеям, приведена в табл. 5.

Расстояния между полями и приёмными пунктами Таблица 5

Поля	Приёмные пункты
1-ый	2-ой	3-ий	4-ый
1-е
2-е
3-е
4-е
5-е

 

Составить такой план перевозок, чтобы транспортные затраты были минимальными. Опорный план найти методом наименьшего элемента. Оптимальный план найти методом потенциалов.

Решение. Проверим баланс между общим объёмом А зелёной массы, вывозимой с полей и суммарной вместимостью В силосных траншей. A = a₁+a₂+a₃+a₄+a₅ = 400+500+700+900+1100 = 3600,

В = b₁+b₂+b₃+b₄ = 1200+600+800+1000 =3600. Так как А = В, то задача является закрытой.

1а					Остатки
	5	6 –	2	2
	9	7 –	4	6
	7	1 600	4	5
	5	2 –	2	4
	6	4 –	3	4
Остатки

1б					Остатки
	5 –	6 –	2 –	2 400
	9	7 –	4	6
	7	1 600	4	5
	5	2 –	2	4
	6	4 –	3	4
Остатки

Определим опорный план методом наименьшего элемента. Среди всех оплат за перевозку тонны зелёной массы с полями к силосным траншеям выберем самое наименьшее. Это оплата перевозки между третьим полем и второй силосной траншеей с₃₂=1. Осуществляем поставку в клетку (3;2).

Определим объём поставки в эту клетку как минимум из остатка объёма зелёной массы 3 поля и остатка вместимости 2 силосной траншеи. Так как зелёная масса ещё не распределялась, то остатки равны начальным значениям массы и вместимости: 700 и 600 тонн. Минимальным будет остаток 600 т. Поставляем в клетку (3;2) 600 т. Пересчитываем остатки: с 3-го поля осталось перевезти 700 – 600 = 100 т, а остаток вместимости 2-ой силосной траншеи стал равным 600 – 600 = 0. 2-ую силосную траншею вычёркиваем из дальнейшего рассмотрения. Как и во втором задании, будем нумеровать таблицы в левом верхнем углу. Выполненные действия отметим в таблице 1а.

Среди всех оплат за перевозку тонны зелёной массы с полей к силосным траншеям в оставшейся части таблицы выберем минимальное. Это оплаты перевозки с₁₃=2, с₁₄=2 и с₄₃=2. Выбираем клетку (1;4). Определим объём поставки в эту клетку. Перевозки с 1-го поля к 4-той силосной траншее ещё не планировались, то остатки равны: для поля 400 т, для траншеи 1000 т. Минимальным будет остаток 400 т. Поставляем в клетку (1;4) 400 т. Пересчитываем остатки: для 1-го поля: 400 – 400 = 0 т, для 4-ой траншеи: 1000 – 400 = 600 т (табл. 1б). Вычёркиваем 1-ое поле из дальнейшего рассмотрения.

Опять среди всех оплат за перевозку тонны зелёной массы с полей к силосным траншеям в оставшейся части таблицы находим минимальное. Это оплаты перевозки с₄₃=2. Выбираем клетку (4;3). Остатки равны: для поля – 900 т, для

1в					Остатки
	5 –	6 –	2 –	2 400
	9	7 –	4 –	6
	7	1 600	4 –	5
	5	2 –	2 800	4
	6	4 –	3 –	4
Остатки

траншеи 800 – т. Минимальным будет остаток 800 т. Поставляем в клетку (4;3) 800 т. Пересчитываем остатки: для поля: 900 – 800 = 100 т, для траншеи: 800 – 800 = 0 т

(табл. 1в). 3-ий пункт вычёркиваем из дальнейшего рассмотрения.

1г					Остатки
	5 –	6 –	2 –	2 400
	9	7 –	4 –	6 –
	7	1 600	4 –	5 –
	5	2 –	2 800	4 –
	6	4 –	3 –	4 600
Остатки				600, 0

1д					Остатки
	5 –	6 –	2 –	2 400
	9	7 –	4 –	6 –
	7	1 600	4 –	5 –
	5 100	2 –	2 800	4 –	100, 0
	6	4 –	3 –	4 600
Остатки				600, 0

Наименьшая оплата перевозки с₄₄=4, с₅₄=4. Выбираем клетку (5;4).Остатки равны: для поля 1100 т, для траншеи 600 т. Минимальным будет остаток 600 т. Пересчитываем остатки (табл. 1г): для поля 1100 – 600 = 500 т, для траншеи 600 – 600 = 0 т. Вычёркиваем 4-ый пункт.

Минимальная оплата перевозки с₄₁=5. Выбираем клетку (4;1). Остатки равны: для поля–100 т, для траншеи – 1200 т. Минимальным будет остаток 100 т. Делаем поставку в клетку (4;1) в объёме100 т. Пересчитываем остатки: для поля 100 – 100 = 0 т, для траншеи 1200 – 100 =1100 т (табл. 1д).

4-ое поле вычёркиваем из дальнейшего рассмотрения.

1е					Остатки
	5 –	6 –	2 –	2 400
	9	7 –	4 –	6 –
	7	1 600	4 –	5 –
	5 100	2 –	2 800	4 –	100, 0
	6 500	4 –	3 –	4 600	500, 0
Остатки	1100, 600			600, 0

Оплата перевозки с₅₁=6. Выбираем клетку (5;1). Остатки равны: поле 500 т, траншея – 1100 т. Минимальным будет остаток 500 т. Поставляем в клетку (5;1) 500 т. Остатки: 500 – 500 = 0 т для поля,

1ж					Остатки
	5 –	6 –	2 –	2 400
	9	7 –	4 –	6 –
	7 100	1 600	4 –	5 –	100, 0
	5 100	2 –	2 800	4 –	100, 0
	6 500	4 –	3 –	4 600	500, 0
Остатки	1100, 600,500			600, 0

1100–500=600 т для траншеи

(табл. 1е). 5-ое поле вычёркиваем.

Оплата перевозки с₃₁=7. Выбираем клетку (3;1). Остатки: поле – 100, траншея – 600 т. Минимальный остаток 100 т. Поставка в клетку (3;1) в объёме 100 т. Пересчитываем

1з					Остатки
	5 –	6 –	2 –	2 400
	9 500	7 –	4 –	6 –
	7 100	1 600	4 –	5 –	100, 0
	5 100	2 –	2 800	4 –	100, 0
	6 500	4 –	3 –	4 600	500, 0
Остатки	1100, 600,500, 0			600, 0

остатки: 100 т для поля, для траншеи 100–100 =500 т (табл. 1ж). вычёркиваем 3-е поле.

Осталась последняя клетка, которая не заполнялась, это клетка (2;1). Проверяем баланс остатков: для поля остаток 500, для траншеи 500 т. Баланс есть. Поставляем в клетку остатки зелёной массы и поля и траншеи в размере 500 т и вычёркиваем из рассмотрения и поле, и траншею(табл. 1з).

Мы получили опорный план, построенный методом наименьшего элемента (табл. 1).

Будем искать оптимальный план. Для этого применим метод потенциалов.

	5	6	2	2 400
	9 500	7	4	6
	7 100	1 600	4	5
	5 100	2	2 800	4
	6 500	4	3	4 600

Методом потенциалов оптимальный план будем находить пошагово. На каждом шаге метода осуществляем переход от одного опорного плана к другому, выполняя следующие действия:

 

1) вычислим потенциалы полей и силосных траншей;

2) вычислим косвенные издержки для свободных клеток;

3) проверим признак оптимальности плана;

4) одну из свободных клеток выбираем для перераспределения зелённой массы;

5) для выбранной клетки строим цикл перераспределения зелёной массы;

6) пометим клетки цикла знаками «+» и «–»;

7) определим объём перераспределения зелёной массы;

8) строим новый опорный план.

Выполняем действие 1). Вычислим потенциалы полей и силосных траншей по заполненным и условно заполненным клеткам.

2а					ui
	5	6	2	2 400
	9 500	7	4	6
	7 100	1 600	4	5
	5 100	2	2 800	4
	6 500	4	3	4 600
vj

Произвольно задаём значение одного из потенциалов, например, положим значение потенциала для первого поля u₁ равным нулю.

Рассматриваем первую строку (табл. 2а).

В ней ищем нерассмотренные заполненные и условно заполненные клетки. Это клетка (1; 4).

По этой клетке определяем потенциал 4-ой

силосной траншеи: v₄ = u₁ + c₁₄ = 0 + 2 = 2.

Больше нерассмотренных заполненных и условно заполненных клеток в первой строке нет. Переходим к последнему вычисленному потенциалу, к потенциалу v₄ = 2. Это потенциал

2б					ui
	5	6	2	2 400
	9 500	7	4 *	6
	7 100	1 600	4	5
	5 100	2	2 800	4
	6 500	4	3	4 600	-2
vj

4-ой силосной траншеи.

Рассматриваем 4-ый столбец (табл. 2б). Находим в этом столбце нерассмотренные заполненные и условно заполненные клетки. Это клетка (5; 4). По этой клетке определяем потенциал 5-ого поля: u₅ = v₄ – c₅₄ = 2 – 4 = –2. Больше нерассмотренных заполненных и условно

заполненных клеток в четвёртом столбце нет. Переходим к последнему вычисленному потенциалу, к потенциалу u₅ = –2. Это потенциал 5-ого поля.

2в					ui
	5	6	2	2 400
	9 500	7	4 *	6
	7 100	1 600	4	5
	5 100	2	2 800	4
	6 500	4	3	4 600	-2
vj

Рассматриваем 5-ую строку (табл. 2в). Находим в этой строке нерассмотренные заполненные и условно заполненные клетки. Это клетка (5; 1). По этой клетке определяем потенциал 1-ой силосной траншеи: v₁ = u₅ + c₅₁ = –2 + 6 = 4. Больше нерассмотренных заполненных и условно заполненных клеток в пятой строке нет.

Переходим к последнему вычисленному потенциалу, к потенциалу v₁ = –2. Это потенциал 1-ой силосной траншеи.

2г					ui
	5	6	2	2 400
	9 500	7	4 *	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj

Рассматриваем 1-ый столбец (табл. 2г). Находим в этом столбце нерассмотренные заполненные и условно заполненные клетки. Это клетки (2; 1), (3; 1) и (4; 1). По этим клеткам определяем потенциалы 2-ого, 3-его и 4-го полей: u₂ = v₁ – c₂₁ = 4 – 9 = –5, u₃ = v₁ – c₃₁ = 4 – 7 = –3, u₄ = v₁ – c₄₁ = 4 – 5 = –1.

Больше нерассмотренных заполненных и условно заполненных клеток в четвёртом столбце нет. Переходим к последним вычисленным потенциалам, к потенциалам u₂ = –5, u₃ = –3 и

u₄ = –1. Это потенциалы 2-ого поля, 3-его поля и 4-ого поля.

Сначала рассмотрим 2-ую строку (табл. 2д). Находим в этой строке нерассмотренные заполненные и условно заполненные клетки. Таких клеток нет.

Переходим к следующему вычисленному потенциалу, к потенциалу u₃ = –3. Это потенциал 3-его поля.

2д					ui
	5	6	2	2 400
	9 500	7	4	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

Рассматриваем 3-ю строку (табл. 2д). Находим в этой строке нерассмотренные заполненные и условно заполненные клетки. Это клетка (3; 2). По этой клетке определяем потенциал 2-ой силосной траншеи: v₂ = u₃ + c₃₂ = –3 + 1 = –2. Больше нерассмотренных заполненных и условно заполненных клеток в третьей строке нет.

2е					ui
	5	6	2	2 400
	9 500	7	4	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

Переходим к следующему вычисленному потенциалу, к потенциалу u₄ = –1. Это потенциал 4-тьего поля.

Рассматриваем 4-ую строку (табл. 2е). Находим в этом строке нерассмотренные заполненные и условно заполненные клетки. Это клетка (4; 3). По этой клетке определяем потенциал

					ui
	5	6	2	2 400
	9 500	7	4	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

3-ей силосной траншеи: v₃ = u₄ + c₄₃ = –1 + 2 = 1. Больше нерассмотренных заполненных и условно заполненных клеток в четвёртой строке нет.

Мы вычислили все потенциалы. Результаты вычислений представлены таблицей 2.

Переходим к выполнению следующего пункта шага метода потенциалов.

2) вычислим косвенные издержки для свободных клеток, которые обозначим Δ_ij.

Косвенные издержки для свободных клеток вычисляем по формуле: Δ_ij = c_ij – (v_j – u_i).Δ₁₁ =5–(4 – 0)=1; Δ₁₂ =6–(-2–0) =8; Δ₁₃ =2 – (1 – 0) = 1; Δ₂₂=7 –(–2+5)=4;

Δ₂₃ = 4 – (1+5) = – 2; Δ₂₄ = 6–(2+5) = – 1; Δ₃₃ = 4 – (1+ 3) = 0; Δ₃₄ = 5 – (2+3)= 0; Δ₄₂=2–(– 2+1) = 3; Δ₄₄=4–(2+1)=1; Δ₅₂ =4 – (–2+2) = 4; Δ₅₃ = 3 – (1+2) = 0.

3) Проверяем признак оптимальности плана: если для всех свободных клеток косвенные издержки положительные (Δ_ij ≥ 0), то опорный план является оптимальным.

План не оптимальный, так как Δ₂₃ = – 2 < 0 и Δ₂₄ = – 1 < 0.

4) Выбираем клетку для перераспределения зелённой массы. Это одна из клеток таблицы, для которой косвенные издержки строго отрицательные. Выбираем клетку (2;3).

5) Для выбранной клетки (2;3) строим цикл перераспределения зелёной массы.

2ж					ui
	5	6	2	2 400
	9 500	7	4 *	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

2з					ui
	5	6	2	2 400
	9 500	7	4 *	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

Выбранную свободную клетку (2;3) включаем в цикл. Далее рассматриваем строку,

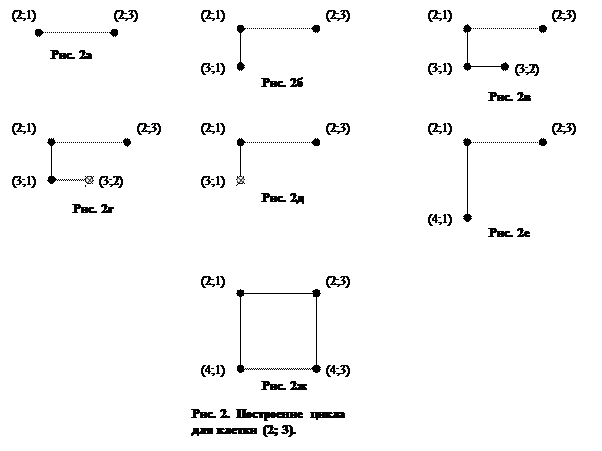
содержащую эту клетку. Это вторая строка. Во второй строке ищем заполненные и условно заполненные клетки (табл. 2ж). Такие клетки есть, это клетка (2;1). Так как она единственная, то её включаем в цикл (рис. 2а) и переходим к ней.

Рассматриваем столбец, содержащий включённую в цикл клетку (2;1). Это первый столбец. В первом столбце находим нерассмотренные заполненные и условно заполненные клетки. Это клетки (3;1), (4;1) и (5;1) (табл. 2з). Выбираем любую из них, например клетку (3;1). Включаем её в цикл (рис. 2б). Переходим к ней.

Рассматриваем строку, содержащую эту клетку. Это третья строка. В третьей строке ищем нерассмотренные заполненные и условно заполненные клетки (табл. 2и). Такие клетки есть, это клетка (3;2). Так как она единственная, то её включаем в цикл (рис. 2в) и переходим к ней.

 

2и					ui
	5	6	2	2 400
	9 500	7	4 *	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

 

Рассматриваем столбец, содержащий клетку (3;2). Это второй столбец. В столбце находим нерассмотренные заполненные и условно заполненные клетки. Таких клеток нет. Вычёркиваем клетку (3;2) из цикла и переходим к предыдущей клетке цикла, к клетке (3;1) (рис. 2г).

2к					ui
	5	6	2	2 400
	9 500	7	4 *	6	-5
	7 100	1 600	4	5	-3
	5 100	2	2 800	4	-1
	6 500	4	3	4 600	-2
vj		-2

Опять рассматриваем третью строку. В третьей строке ищем нерассмотренные заполненные и условно заполненные клетки (табл. 2и). Клетки (3;1) и (3;2) уже рассматривались, других клеток нет. Вычёркиваем клетку (3;1) из цикла и переходим к предыдущей клетке цикла, к клетке (2;1) (рис. 2д). Снова рассматриваем столбец, содержащий клетку (2;1). В первом столбце находим нерассмотренные заполненные и условно заполненные клетки. Это клетки (4;1) и (5;1), клетки (2;1) и (3;1) уже рассматривались (табл. 2з). Выбираем любую из них, например клетку (4;1). Включаем её в цикл (рис. 2е). Переходим к ней. Рассматриваем строку, содержащую клетку (4;1). Это четвёртая строка (табл. 2к). В этой строке есть заполненная клетка, которая располагается в том же столбце, что и начальная клетка цикла, клетка (2; 3). Это клетка (4; 3). Автоматически её включаем в цикл, и цикл замыкаем (рис. 2е).

Построенный цикл для свободной клетки (2; 3) изображён на рисунке 2ж.

6) Пометим клетки цикла знаками «+» и «–». Помечать клетки цикла начнём со свободной клетки цикла, клетки (2; 3). Её пометим знаком «+». Далее, двигаясь по циклу в направлении его построения, помечаем остальные клетки цикла, чередуя знаки (рис. 3). 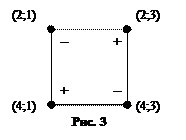Клетку (2; 1) пометим знаком «–», клетку (4;1) знаком «+», клетку (4;3) знаком «–». В клетки, помеченные знаком «+» зелёную массу будем добавлять, а из клеток, помеченных знаком «–» зелёную массу будем забирать. Клетками, откуда зелёная масса забирается, будут (2;1) и (4;3).

7) Определим объём перераспределения зелёной массы. Объём перераспределения зелённой массы ΔV равняется наименьшему из объёмов отрицательных клеток цикла. В клетке (2; 1) объём поставки зелёной массы равняется 500 т, а в клетке (4;3) – 800 т (рис. 5). Поэтому объём перераспределения зелёной массы ΔV равен: ΔV = min{500; 800}= 500 т.

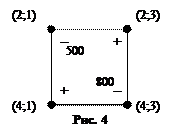8) Строим новый опорный план. Сначала пересчитываем объёмы зелёной массы для клеток цикла (табл. 3): для клетки (2; 3) новый объём равен

x₂₃ = 0 + 500 = 500 т, для клетки (2; 1) новый объём равен

					ui
	5	6	2	2 400
	9	7	4 500	6	-3
	7 100	1 600	4	5	-3
	5 600	2	2 300	4	-1
	6 500	4	3	4 600	-2
vj		-2

x₂₁ = 500 – 500 = 0 т, для клетки (4; 1) новый объём равен x₄₁ = 100 + 500 = 600 т, для клетки (4; 3) новый объём равен x₄₃ = 800 – 500 = 300 т. Объём клетки (2; 1) стал равным нулю, её переводим в ранг свободных, а клетку (2; 3) переводим в ранг заполненных. Объёмы остальных клеток таблицы, не вошедших в цикл, не меняются: x₁₄ = 400, x₃₁ = 100, x₃₂ = 600, x₅₁ = 500, x₅₄ = 600 (табл. 3). Шаг метода потенциалов закончен. Переходим к новому шагу. В качестве опорного рассматриваем план, соответствующий таблице 3.

1) Вычислим потенциалы полей и силосных траншей (табл. 3).

2) Вычислим косвенные издержки для свободных клеток: Δ₁₁ =5–(4–0)=1; Δ₁₂ =6–(–2–0) =8;

Δ₁₃ =2–(1–0)=1; Δ₂₁ =9–(4+3) = 2; Δ₂₂ =7–(–2+3)=6; Δ₂₄=6–(2+3)=1; Δ₃₃=4–(1+3)=0; Δ₃₄=5–(2+3) =0; Δ₄₂=2–(–2+1)=3; Δ₄₄ =4–(2+1) =1; Δ₅₂=4–(–2+2)=4; Δ₅₃=3–(1+2) = 0.

3) Проверим признак оптимальности плана. План оптимальный, так как для всех свободных клеток косвенные издержки больше либо равны нуля (Δ_ij ≥ 0).

По таблице 3 выписываем оптимальный план: X* = .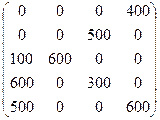

Для оптимального плана рассчитываем суммарные транспортные издержки:

Z_min = 2∙400 +4∙500 +7∙100 +1∙600 +5∙600+ +2∙300 +6∙500 +4∙600 = 13100.

Выписываем ответ: X* = 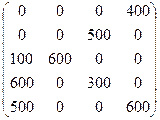; Z_min= 13100.