Алгоритмы циклической структуры

ЛИНЕЙНЫЙ АЛГОРИТМ

Линейный алгоритм - это такой, в котором все операции выполняются последовательно одна за другой (рис. 1).

 

Рис. 1. Размещение блоков в линейном алгоритме

ЗАДАНИЯ

ПРИМЕР 1. Вычислить площадь и периметр треугольника. (Для нахождения площади можно воспользоваться формулой Герона: 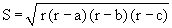, где r - полупериметр)

ПРИМЕР 2. Вычислите площадь прямоугольника по его сторонам.

ПРИМЕР 3. Заданы длины двух катетов в прямоугольном треугольнике. Найти длину гипотенузы, площадь треугольника.

ПРИМЕР 4. составить блок-схему алгоритма сложения двух чисел a и b.

ПРИМЕР 5. составить блок-схему алгоритма нахождения суммы двух обыкновенных дробей где b и d отличны от нуля.

ПРИМЕР 6. Определить площадь и длину второго катета прямоугольного треугольника, если известны длина одного катета и длина гипотенузы.

ПРИМЕР 7. Определить длину ломаной линии, состоящей из трех звеньев, если известны координаты вершин (Длина отрезка по координатам вычисляется по формуле: )

ПРИМЕР 8. Известны координаты вершин треугольника. Определить периметр и площадь треугольника.

ПРИМЕР 9. Хозяин хочет оклеить обоями квартиру. Определить количество необходимых рулонов и затрат на их приобретение.

ПРИМЕР 10. Найти корни системы двух алгебраических уравнений с двумя неизвестными по формуле Крамера, считая, что система разрешима.

ПРИМЕР 11. В некотором треугольнике основание больше высоты на заданную величину d. Определить значение высоты и основания, если известна величина площади треугольника.

РАЗВЕТВЛЕННЫЙ АЛГОРИТМ

Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. В блок-схемах разветвленные алгоритмы изображаются так, как показано на рис. 2 - 3.

Рис. 2 Фрагмент алгоритма	Рис. 3 Пример разветвления

ЗАДАНИЯ

ПРИМЕР 1. Прием на работу ведется на конкурсной основе. Условия приема: человек должен быть моложе 42 лет и иметь стаж более20 лет

ПРИМЕР 2. Составьте блок-схему алгоритма вычисления значения функции по формуле:

ПРИМЕР 3. Составьте блок-схему алгоритма решения квадратного уравнения.

ПРИМЕР 4. Составьте блок-схему алгоритма вычисления значения функции

ПРИМЕР 5. Постройте блок-схему алгоритма линейного уравнения.

ПРИМЕР 6. Вычислить и вывести на экран корень квадратный из положительного числа Х, значение которого не превышает 1000. В случае отрицательного числа никаких вычислений в программе не производится.

ПРИМЕР 7. Даны действительные положительные числа a, b, c, x, y. Выяснить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x, y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.

ПРИМЕР 8. Число делится на 3, если сумма его цифр делится на 3. Проверить этот признак на примере заданного трехзначного числа.

ПРИМЕР 9. Можно ли коробку размером упаковать в посылку размером . «Углом» укладывать нельзя.

ПРИМЕР 10. Построить блок-схему алгоритма: даны 3 целых числа. Вывести наибольшее из них

ПРИМЕР 11. Построить алгоритм (нарисовать блок-схему), осуществляющий сортировку значений трех переменных А, В, С по возрастанию.

 

АЛГОРИТМЫ ЦИКЛИЧЕСКОЙ СТРУКТУРЫ

Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры. На рис. 4 изображен цикл с предусловием, а на рис. 5 - цикл с постусловием, которые называют условными циклическими алгоритмами. Нетрудно заметить, что эти циклы взаимозаменяемы и обладают некоторыми отличиями.

· в цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием - после тела цикла;

· в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу;

· в цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием - условие выхода из цикла.

Рис. 4. Алгоритм циклической структуры с предусловием	Рис. 5 Алгоритм циклической структуры с постусловием

При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла.

Кроме того, существует так называемый безусловный циклический алгоритм (рис. 6), который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла.

Рис. 6. Алгоритм циклической структуры без условия

Выполнение безусловного циклического алгоритма начинается с присвоения переменной i стартового значения in. Затем следует проверка, не превосходит ли переменная i конечное значение iк. Если превосходит, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и переменная i меняет свое значение в соответствии с указанным шагом di. Далее, снова производится проверка значения переменной i и алгоритм повторяется. Понятно, что безусловный циклический алгоритм можно заменить любым условным. Например, так как показано на рис. 7.

Рис. 7. Условный циклический алгоритм с известным числом повторений

 

Отметим, что переменную i называют параметром цикла, так как это переменная, которая изменяется внутри цикла по определенному закону и влияет на его окончание.

Рассмотрим использование алгоритмов циклической структуры на конкретных примерах.

 

ЗАДАНИЯ

 

ПРИМЕР 1. Найти наибольший общий делитель (НОД) двух натуральных чисел А и В. (Для решения поставленной задачи необходимо воспользоваться алгоритмом Евклида)

ПРИМЕР 2. Имеются чёрный, белый и синий ящики. В полосатом ящике находятся черные, белые и синие шары, по 5 шаров каждого цвета. Выполните сортировку шаров, поместив белые шары в белый ящик, черные в черный, синие в синий.

ПРИМЕР 3. Разработать блок-схему алгоритма Евклида, определяющего наибольший общий делитель (НОД) двух натуральных чисел A и B.

В основе алгоритма Евклида лежит правило: НОД(A,B)= НОД(min(A,B), |A-B|), где НОД(A,B) — наибольший общий делитель двух натуральных чисел A и B.

ПРИМЕР 4. Дано не менее трех различных натуральных чисел, за которыми следует 0. Определить три наибольших числа среди них.

ПРИМЕР 5. Вводится последовательность чисел, 0 – конец последовательности. Определить, содержит ли последовательность хотя бы два равных соседних числа.

ПРИМЕР 6. Построить блок – схему для решения задачи: Средняя скорость молекул в сосуде 1000м/с. В каждый следующий час скорость молекул увеличивалась на 20м/с, чем в предыдущий. Какова будет скорость молекул через 10 часов?

ПРИМЕР 7. Создать блок-схему алгоритм пробега 9 кругов вокруг стадиона на уроке физкультуры.

ПРИМЕР 8. Создать блок-схему алгоритма для сбора денег на покупку видеоигры стоимостью 200 грн.

ПРИМЕР 9. Составить алгоритм с помощью которого можно поточить 20 карандашей из коробки.

ПРИМЕР 10. Составьте алгоритм приготовления оладьей.

ПРИМЕР 11. Некоторая бактерия через каждую минуту делится на две точно таких же бактерии. Определите, за сколько минут число бактерий станет равно N, если в начальный момент времени имеется только одна бактерия.

 

ОТЧЕТ О РАБОТЕ

1). Титульный лист;

2). Цель лабораторной работы;

3). Ход работы с результатами выполнения.