Діагностична контрольна робота з алгебри
У 10-х класах
Зміст завдань відповідає діючій програмі для загальноосвітніх навчальних закладів.
Пропонується 20 варіантів роботи.
Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.
У І частині контрольної роботи запропоновано п’ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки один правильний. Завдання вважається виконаним правильно, якщо учень указав тільки одну літеру, якою позначений правильний варіант відповіді. Правильна відповідь за кожне із завдань 1-5 – оцінюється одним балом.
ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв’язання повинно мати короткий запис рішення без обґрунтування. Правильне розв’язання кожного із завдань цього блоку оцінюється двома балами.
ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв’язання якого повинно мати розгорнутий запис рішення з обґрунтуванням. Правильне розв’язання завдання цього блоку оцінюється трьома балами.
Сума балів нараховується за правильно виконані учнем завдання відповідно максимально можливій кількості запропонованих балів для кожного блоку (5; 4; 3-всього 12балів).
Контрольна робота розрахована на 45 хвилин. Роботи виконуються у зошитах або на окремих аркушах. При виконанні роботи необхідно указати номер завдання, текст завдань переписувати не обов’язково.
Примітка. У тексти завдань можна вносити корективи: збільшити (зменшити) кількість завдань або посилити (послабити) ступінь складності. Корективи обов’язково обґрунтувати.
Зразок підпису роботи
Діагностична контрольна робота з алгебри
учня (учениці) ____10_____ класу
______________________________
назва навчального закладу
______________________________
прізвище ім’я в родовому відмінку
Варіант _____
Звіт з математики
ЗНЗ_________________________________________
Табл.1. Кількісний звіт
| Кіл-ть учнів | Писало | Результати | |||||||
| І рівня | ІІ рівня | ІІІ рівня | ІV рівня | ||||||
| кільк. | % | кільк. | % | кільк. | % | кільк. | % | ||
Табл.2. Якісний звіт
| Всього учнів | Писало | Правильна відповідь завдань у % | Кількість набраних балів у % | Кількість набраних балів у % | Кількість набраних балів у % | ||||||||||||
| Кіл-ть | % | 6 завдання | 7 завдання | 8 завдання | |||||||||||||
Аналітичний звіт.
Відзначити який матеріал засвоєно якісно.
Які допущені помилки. Причини виникнення та шляхи їх подолання.
Примітка. Якщо у тексти завдань були внесені корективи, необхідно надіслати текст з обов’язковим обґрунтуванням.
Директор підпис прізвище, ініціали
Печатка
Виконавець
Варіант 1
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Знайдіть добуток нерівностей 7 > 3 і 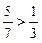 .
.
А) 5 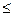 1; Б) 5 > 1; В) 5 ≥ 1; Г) 5 < 1.
1; Б) 5 > 1; В) 5 ≥ 1; Г) 5 < 1.
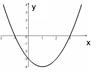 2. Вкажіть за графіком нулі функції:
2. Вкажіть за графіком нулі функції:
А) –3; 3; Б) –1; 3; В) –1; –3; Г) –3;–1.
3. При якому значенні х вираз 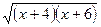 має зміст?
має зміст?
А) 4; Б) –5; В) –5,8; Г) –4,5.
4. Знайдіть суму нескінченої геометричної прогресії, якщо 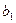 = 14, а
= 14, а 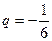 .
.
А) –12; Б) –84; В) 16,8; Г) 12.
5. Спростіть вираз 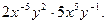
А) 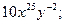 Б)
Б) 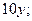 В)
В) 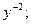 Г)
Г) 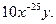
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть нерівність 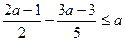 .
.
7. Побудуйте графік функції 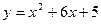 і визначте, на яких проміжках ця функція зростає, а на яких спадає.
і визначте, на яких проміжках ця функція зростає, а на яких спадає.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Через скільки років капітал покладений до банку під 8% річних, збільшиться у 2 рази?
Варіант 2
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Знайдіть добуток нерівностей 0,5 < 6 і 4 < 5.
А) 2 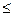 3; Б) 20 < 30; В) 2 < 30; Г) 2 > 3.
3; Б) 20 < 30; В) 2 < 30; Г) 2 > 3.
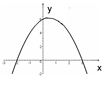 2. Вкажіть за графіком нулі функції
2. Вкажіть за графіком нулі функції
А) –2; 3 Б) –2; 6; В) 6; 3; Г) 3; 6.
3. При якому значенні х вираз 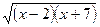 має зміст?
має зміст?
А) –6; Б) –3; В) –5; Г) 10.
4. Знайдіть суму нескінченої геометричної прогресії, якщо 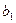 = 15, а
= 15, а 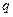 =
= 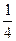 .
.
А) 20; Б) 60; В) –20; Г) 11,25.
5. Спростіть вираз 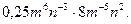
А) 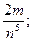 Б)
Б) 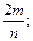 В)
В) 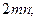 Г)
Г) 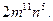
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть нерівність 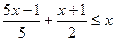 .
.
7. Побудуйте графік функції 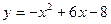 і визначте, на яких проміжках ця функція зростає, а на яких спадає.
і визначте, на яких проміжках ця функція зростає, а на яких спадає.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Через скільки років капітал, покладений до банку під 4% річних, збільшиться у 2 рази?
Варіант 3
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв’яжіть систему нерівностей і вкажіть її найбільший цілий розв'язок 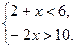
А) 3; Б) 4; В) −5; Г) −6.
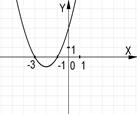 2. За даним графіком визначте проміжки, на яких функція приймає додатні значення.
2. За даним графіком визначте проміжки, на яких функція приймає додатні значення.
А) 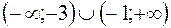 ; Б)
; Б) 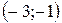 ;
;
В)  ; Г)
; Г)  .
.
3. При якому значенні х вираз 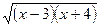 має зміст?
має зміст?
А) 4; Б) −3; В) 2; Г) −1.
4. Знайдіть перший член нескінченої геометричної прогресії за відомою її сумою S=36 та знаменником 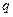 =
= 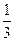 .
.
А) −24; Б) 54; В) 24; Г) 12.
5. Запишіть одночлен у стандартному вигляді 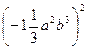 .
.
А) 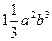 ; Б)
; Б) 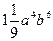 ; В)
; В) 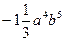 ; Г)
; Г) 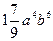 .
.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть систему нерівностей 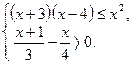
7. Скоротіть дріб 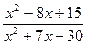 .
.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Із пунктів А і В, розташованих на відстані 100 км, назустріч один одному одночасно виїхали 2 велосипедисти. Через 4 години вони зустрілися. Після зустрічі швидкість першого велосипедиста, що рухався із А до В, зросла на 5 км/год, а швидкість другого - на 10 км/год. Знайдіть початкову швидкість другого велосипедиста, якщо перший прибув до пункту В на 1 годину раніше, ніж другий до пункту А.
Варіант 4
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв’яжіть систему нерівностей і вкажіть її найбільший цілий розв'язок 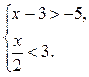
А) 6; Б) 5; В) −2; Г) −1.
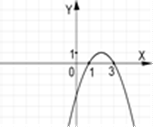 2. За даним графіком визначте проміжки, на яких функція приймає додатні значення.
2. За даним графіком визначте проміжки, на яких функція приймає додатні значення.
А) 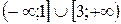 ; Б)
; Б) 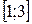 ;
;
В) 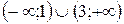 ; Г)
; Г) 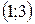 .
.
3. При якому значенні х вираз 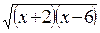 має зміст?
має зміст?
А) 4; Б) 3; В) −1; Г) 10.
4. Знайдіть перший член нескінченної геометричної прогресії за відомою її сумою S=16 та знаменником 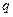 =
= 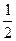 .
.
А) 32; Б) 8; В) – 8; Г) −32.
5. Запишіть одночлен у стандартному вигляді 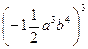 .
.
А) 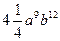 ; Б)
; Б) 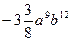 ; В)
; В) 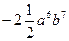 ; Г)
; Г) 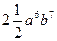 .
.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть систему нерівностей 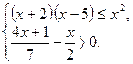
7. Скоротіть дріб 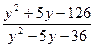 .
.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Із пунктів А і В, розташованих на відстані 50 км, назустріч один одному одночасно виїхали 2 пішоходи. Через 5 годин вони зустрілися. Після зустрічі швидкість першого пішохода, що рухався із А до В, зменшилася на 1 км/год. Знайдіть початкову швидкість першого пішохода, якщо він прибув до пункту В на 2 години раніше, ніж другий - до пункту А.
Варіант 5
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Виконайте дії 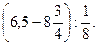
А) 18; Б) 0,28125; В) 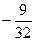 ; Г) −18;
; Г) −18;
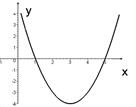 2. За даним графіком визначте проміжки, на яких функція приймає додатні значення:
2. За даним графіком визначте проміжки, на яких функція приймає додатні значення:
А) (–∞; 1)  (5; ∞); Б) (1; 5);
(5; ∞); Б) (1; 5);
В) (1; 5]; Г) (0; ∞).
3. Яке число є розв’язком нерівності 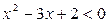 ?
?
А) 4; Б) 1,5; В) 9; Г) 10.
4. Знайдіть суму п’яти перших членів геометричної прогресії (bn), якщо 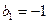 , а
, а 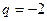 .
.
А) 11; Б) −11; В) 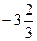 ; Г)
; Г) 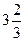 .
.
5. Розв’яжіть рівняння 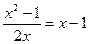 .
.
А) −1; Б) 15; В) −1; −15; Г) 1.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть нерівність 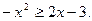
7. Члени геометричної прогресії – натуральні числа. Третій член дорівнює кубу першого. Сума першого і третього членів у 5 разів більша від першого члену. Знайдіть цю прогресію і суму п’яти її членів.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Два басейни однієї місткості одночасно почали наповнюватися водою. У перший басейн надходить щогодини на 30 м3 більше води, ніж у другий. У деякий момент у двох басейнах разом було стільки води, скільки вміщується води в кожному з них. Після цього через 2 години 40 хвилин наповнився перший басейн, а ще через 3 години 20 хвилин - другий. Скільки води надходило щогодини у кожен басейн?
Варіант 6
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Виконайте дії 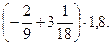
А) 6,125; Б) 5,1; В) 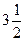 ; Г) 5,6.
; Г) 5,6.
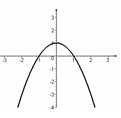 2. За даним графіком визначте проміжки, на яких функція приймає додатні значення:
2. За даним графіком визначте проміжки, на яких функція приймає додатні значення:
А) (–∞; –1); Б); (–1; 1);
В) (1; +∞); Г) [–1; 1].
3. Яке число є розв’язком нерівності 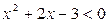 ?
?
А) 4; Б) 3; В) 9; Г) 0.
4. Знайдіть суму чотирьох перших членів геометричної прогресії (bn), якщо 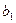 =
= 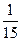 , а
, а 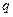 =
= 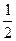 .
.
А) 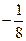 ; Б) 8; В)
; Б) 8; В) 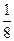 ; Г)
; Г) 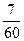 .
.
5. Розв’яжіть рівняння 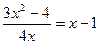 .
.
А) 2; Б) −2; В) 4; Г) −4.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть нерівність 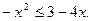
7. Добуток перших двох членів арифметичної прогресії дорівнює 18, а добуток другого і третього членів дорівнює 54. Знайдіть шостий член цієї прогресії і суму шести членів.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Кожна з двох друкарок передруковувала по 72 сторінки рукопису. Перша друкарка надрукувала 6 сторінок за той же час, за який друга надрукувала 5 сторінок. Скільки сторінок друкувала кожна друкарка за годину, якщо перша закінчила роботу на 1,5 години раніше за другу?
Варіант 7
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв’яжіть рівняння 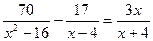 .
.
А) 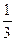 ; −2; Б) 2;
; −2; Б) 2; 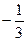 ; В) −1;
; В) −1; 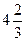 ; Г) −4; 4.
; Г) −4; 4.
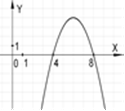 2. За даним графіком визначте проміжки, на яких функція приймає від’ємні значення:
2. За даним графіком визначте проміжки, на яких функція приймає від’ємні значення:
А) 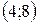 ; Б)
; Б) 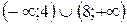 ;
;
В) 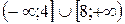 ; Г)
; Г) 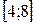 .
.
3. Яке число є розв’язком нерівності 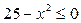 ?
?
А) 4; Б) 3; В) 9; Г) 0.
4. Знайдіть другий член геометричної прогресії 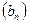 , якщо
, якщо 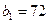 , а
, а 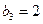 та
та 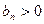 .
.
А) 12; Б) 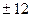 ; В) −12; Г)
; В) −12; Г) 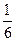 .
.
5. Знайдіть медіану вибірки 2,4; 2,7; 2,6; 2,4; 2,7; 3,0.
А) 2,65; Б) 2,7; В) 2,5; Г) 2,58.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Оцініть значення виразів 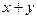 ;
; 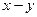 ;
; 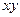 , якщо:
, якщо: 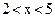 і
і 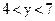 .
.
7. Знайдіть чотири числа, що утворюють спадну геометричну прогресію, у якій сума крайніх чисел дорівнює 112, а сума середніх дорівнює 48.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Якщо до чисельника звичайного дробу додати 1, а до знаменника додати 3, то дістанемо дріб, який дорівнює 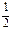 . Якщо ж від чисельника відняти 1, а до знаменника додати 1, то дістанемо дріб, при множенні якого на початковий, матимемо
. Якщо ж від чисельника відняти 1, а до знаменника додати 1, то дістанемо дріб, при множенні якого на початковий, матимемо 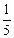 . Знайдіть початковий дріб.
. Знайдіть початковий дріб.
Варіант 8
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв’яжіть рівняння 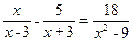 .
.
А) −3; 3; Б) −1; 3; В) 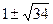 ; Г) −1.
; Г) −1.
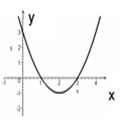 2. За даним графіком визначте проміжки, на яких функція приймає від’ємні значення:
2. За даним графіком визначте проміжки, на яких функція приймає від’ємні значення:
А) (1; 3); Б) (–∞; 1) (3; ∞);
В) (–∞; 2); Г) [1; 3].
3. Яке число є розв’язком нерівності 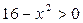 ?
?
А) 4; Б) 3; В) 9; Г) 10.
4. Знайдіть другий член зростаючої геометричної прогресії 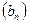 , якщо
, якщо 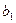 =
= 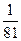 , а
, а 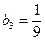 .
.
А) 3; Б) 27; В) 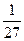 ; Г) −3.
; Г) −3.
5. Знайдіть медіану вибірки 10; 11; 12; 8; 11; 8.
А) 12; Б) 11; В) 10,5; Г) 10.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Оцініть значення виразів 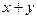 ;
; 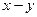 ;
; 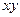 , якщо:
, якщо: 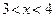 і
і 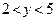 .
.
7. Знайдіть чотири числа, що утворюють зростаючу геометричну прогресію, знаючи, що сума крайніх чисел дорівнює 35, а сума середніх дорівнює 30.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Якщо до чисельника звичайного дробу додати 2, а до знаменника додати 3, то значення дробу не зміниться. Якщо ж до чисельника додати 1, а до знаменника додати 6, то значення дробу зменшиться на 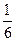 . Знайдіть цей дріб.
. Знайдіть цей дріб.
Варіант 9
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

 1. Які з проміжків є розв'язком нерівності
1. Які з проміжків є розв'язком нерівності 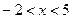 ?
?
А) Б)
 | |||
 | |||
В) Г)
2. Вкажіть область значень функції у = (х–1)2 –3.
А) 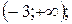 Б)
Б) 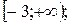 В)
В) 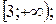 Г)
Г) 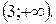
3. Розв׳яжіть нерівність 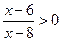 .
.
А) (−∞; 6)U(8; +∞); Б) [6; 8];
В) (−∞; 6]U[8; +∞); Г) (6; 8).
4. Банк сплачує своїм вкладникам 9% річних. Скільки грошей треба покласти в банк, щоб через рік отримати 900 грн. прибутку?
А) 5000 грн.; Б) 10 000 грн.; В) 7500 грн.; Г) 6000 грн.
5. У скриньці 5 чорних і 7 білих кульок. Із скриньки навмання виймається 1 кулька. Знайдіть ймовірність того, що ця кулька біла.
А) 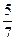 ; Б)
; Б) 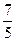 ; В)
; В) 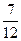 ; Г)
; Г) 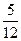 .
.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть нерівність 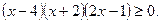
7. Розв'яжіть систему рівнянь 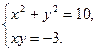
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Сума першого і третього членів арифметичної прогресії дорівнює 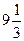 , а різниця між першим і третім дорівнює
, а різниця між першим і третім дорівнює 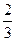 . Знайдіть четвертий член і номер члена, що дорівнює -6.
. Знайдіть четвертий член і номер члена, що дорівнює -6.
Варіант 10
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

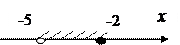
 1. Які з проміжків є розв'язком нерівності -5
1. Які з проміжків є розв'язком нерівності -5 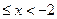 ?
?
А) Б)
 |  |
В) Г)
2. Вкажіть область значень функції у =−(х + 1)2 +2.
А) 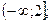 Б)
Б) 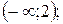 В)
В) 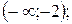 Г)
Г) 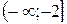 .
.
3. Розв׳яжіть нерівність 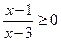 .
.
А) (−∞; 1]U(3; +∞); Б) [1; 3];
В) (−∞; 1]U[3; +∞); Г) (1; 3).
4. Вкладник поклав до банку 6000 грн. під 9% річних. Скільки буде на його рахунку через рік?
А) 6540 грн.; Б) 6720 грн.; В) 6820 грн.; Г) 7100 грн.
5. У скриньці 6 червоних і 5 синіх кульок. Із скриньки навмання виймається 1 кулька. Знайдіть ймовірність того, що ця кулька синя.
А) 0; Б) 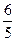 ; В)
; В) 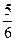 ; Г)
; Г) 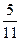 .
.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть нерівність 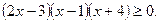
7. Розв'яжіть систему рівнянь 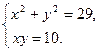
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Сума першого і другого членів арифметичної прогресії дорівнює 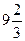 , а різниця між першим членом і різницею цієї прогресії
, а різниця між першим членом і різницею цієї прогресії 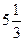 . Знайдіть третій член і номер члена, що дорівнює 191.
. Знайдіть третій член і номер члена, що дорівнює 191.
Варіант 11
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв’яжіть систему нерівностей 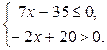 і вкажіть її найбільший натуральний розв’язок.
і вкажіть її найбільший натуральний розв’язок.
А) 4; Б) 5; В) 10; Г) 0.
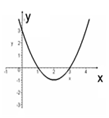 2. За даним графіком визначте проміжки зростання функції.
2. За даним графіком визначте проміжки зростання функції.
А) [2; ∞); Б) (–∞; 2];
В) (–∞; 1) (3; ∞); Г) (1; 3).
3. Розв׳яжіть нерівність 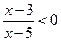 .
.
А) (– ∞; 3)U(5; +∞); Б) [3; 5];
В) (– ∞; 3]U[5; +∞); Г) (3; 5).
4. Визначте кількість членів арифметичної прогресії (аn), якщо 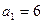
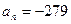 ,
, 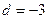 .
.
А) 94; Б) 95; В) 97; Г) 96.
5. На уроці було 16 дівчат та 10 хлопців. На перерву вийшли 12 учнів. Яка з наведених подій є неможливою?
А ) на перерву не вийшли дівчата;
Б) на перерву вийшли тільки дівчата;
В) на перерву вийшли і дівчата і хлопці;
Г) на перерву вийшли всі хлопці.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть систему нерівностей 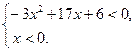
7. Дослідіть функцію на парність 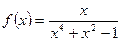 .
.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Розв'яжіть рівняння на інтервалі 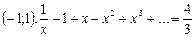 .
.
Варіант 12
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв’яжіть систему нерівностей 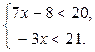 і вкажіть її найбільший натуральний розв’язок.
і вкажіть її найбільший натуральний розв’язок.
А) 4; Б) – 7; В) 3; Г) 1.
2. За даним графіком визначте проміжки зростання функції.
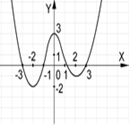 А)
А) 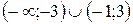 ; Б)
; Б) 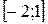 ;
;
В) 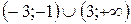 ; Г)
; Г) 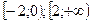 .
.
3. Розв׳яжіть нерівність 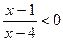 .
.
А) (– ∞; 1)U(4; +∞); Б) [1; 4];
В) (– ∞; 1]U[4; +∞); Г) (1; 4).
4. Визначте кількість членів арифметичної прогресії (аn), якщо 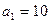 ,
, 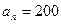 ,
, 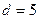 .
.
А) 37; Б) 39; В) 43; Г) 45.
5. На уроці було 16 дівчат та 10 хлопців. На перерву вийшли 18 учнів. Яка з наведених подій є вірогідною?
А ) на перерву вийшли тільки дівчата;
Б) на перерву вийшли і дівчата і хлопці;
В) на перерву не вийшли дівчата;
Г) на перерву вийшли тільки хлопці.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Розв'яжіть систему нерівностей 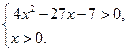
7. Дослідіть функцію на парність 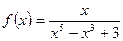 .
.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Розв'яжіть рівняння на інтервалі 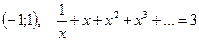 .
.
Варіант 13
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв׳яжіть нерівність x +14 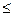 7 x + 12.
7 x + 12.
А) х  [
[ 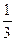 ; +∞); Б) x
; +∞); Б) x  (–∞;
(–∞; 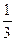 ]; В) х
]; В) х  (
(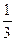 ; +∞); Г) х
; +∞); Г) х  [–4; +∞).
[–4; +∞).
За даним графіком визначте проміжки спадання функції.
А) (–∞; 1)U(3; +∞); Б) [2; +∞);
В) (–∞; 2]; Г) (1; 3).
3. Розв׳яжіть нерівність (х – 1) х > 0.
А) (–∞; 0)U(1; +∞); Б) [0; 1];
В) (–∞; 0]U[1; +∞); Г) (0; 1).
4. Шостий член арифметичної прогресії дорівнює 17, різниця її дорівнює 5. Знайдіть п’ятий член цієї прогресії.
А) 12; Б) 22; В) 37; Г) 105.
5. На придбання спортивного інвентарю було витрачено 1800 грн., з яких 26% - на футбольні м’ячі. Скільки грошей було витрачено на м’ячі?
А) 480 грн.; Б) 468 грн.; В) 454 грн.; Г) 420грн.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
6. Спростіть вираз 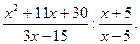
7. При яких значеннях х вираз 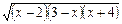 має зміст.
має зміст.
ІІІ частина (3 бали)
Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Із пунктів А і В, розташованих на відстані 50 км, назустріч один одному вийшли одночасно два пішоходи. Через 5 год вони зустрілися. Після зустрічі швидкість першого пішохода, що йде з А до В, зменшилася на 1 км/год, а швидкість другого – зросла на 1 км/год. Знайдіть початкову швидкість першого пішохода, якщо він прибув до пункту В на 2 год раніше, ніж другий – до пункту А.
Варіант 14
І частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
1. Розв׳яжіть нерівність x + 23 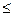 9 x + 17.
9 x + 17.
А) x  [–2; +∞); Б) х
[–2; +∞); Б) х  [
[ 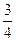 ; +∞); В) х
; +∞); В) х  (–∞;
(–∞; 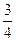 ]; Г) х
]; Г) х  (–∞; 2].
(–∞; 2].






