Распределение элементов по модулям

 

После определения числа модулей каждого типа необходимо получить такое распределение элементов схемы по микросхемам, при котором число соединений между ними будет минимально. Для решения этой задачи может быть использован какой-либо последовательный алгоритм компоновки [3, 4], на каждом шаге которого выбирается один из нераспределенных элементов и приписывается к очередной ИМС. Тактика назначения элементов основана на принципе максимальной связанности назначаемого элемента с элементами, ранее помещенными в рассматриваемую ИМС. При назначении должны учитываться структура ИМС и типы элементов.

Распределение начнем с микросхем 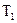, которых имеется x₁ штук.

Структура ИМС 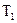описывается вектором , причем 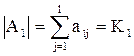. Выделим из исходной схемы элементы, которые могут быть помещены в микросхемы типа 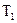. Очевидно, они определяются множеством

, .

Для назначения выбирается тот из элементов , который имеет наибольшее суммарное число соединений с элементами, уже помещенными с ИМС и наименьшее число соединений с остальными элементами из множества 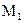. В одинаковых ситуациях выбирается элемент с меньшим номером. Процесс компоновки ИМС продолжается до тех пор, пока или все элементы будут заняты, или на некотором шаге S < K_l среди нераспределенных элементов отсутствуют элементы, отвечающие составу микросхемы. После этого процесс продолжается для остальных T₁, а затем для T₂, … T_m.

 

ПРИМЕР 1.2

 

В примере 1.1 получено x₁ = 3 ИМС типа 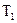, x₂ = 1 ИМС 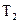и x₃ = 1 ИМС . Требуется распределить элементы по ИМС, используя критерий минимума числа связей между ними.

Решение

При распределении элементов по корпусам микросхем можно было учитывать только выполняемые ими функции. Тогда одним из вариантов покрытия будет схема, представленная на рис.1.4. Число связей между модулями в ней равно 12-ти.

Однако анализ этого результата показывает, что число связей между модулями можно сократить. Для этого необходимо реализовать следующий подход.

1) Из схемы рис.1.1 выделим множество базовых функциональных элементов , которые могут быть помещены в микросхемы типа T_l:

.

Первым в микросхему помещаем элемент e₅, имеющий с остальными максимальное число связей – три; затем в нее назначаем связанные с e₅ элементы: трехвходовый e₂ и двухвходовый e₃. В результате 1-я ИМС 1-го типа будет включать .

Для компоновки 2-й микросхемы этого же типа осталось множество базовых функциональных элементов . . 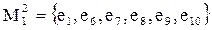Первым в ИМС попадает элемент e₆, затем двухвходовые e₈ и e₉. Получим набор 2-й ИМС .

При компоновке 3-й микросхемы 1-го типа – множество элементов будет 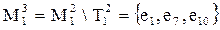. В соответствии с алгоритмом помещаем в нее элементы e₁ и e₇. При этом место t₁ остается незанятым, поскольку все элементы данного типа распределены.

2) Переходим к компоновке микросхем 2-го и 3-го типов – 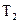и . Пользуясь алгоритмом, получим, что элементы множества 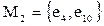назначаются в ИМС , а оставшийся четырехвходовый триггер попадает в с одним незанятым местом . Избыточность покрытия также равна .

Получено распределение элементов по микросхемам. Теперь на основании исходной схемы (рис.1.1) можно сформировать вариант соединения корпусов ИМС, реализующий эту схему. Он представлен на рис.1.5.

В данном варианте число электрических цепей между отдельными ИМС получилось равным девяти, что на три цепи меньше, чем в результате, представленном на рис.1.4. Потому при прочих одинаковых показателях, по данному критерию результат на рис.1.5 лучше. Его и надо принять за решение поставленной задачи покрытия.

 

 

ДОМАШНЕЕ ЗАДАНИЕ

 

2.1. Ознакомиться с методами решения задачи покрытия функциональных схем.

2.2. Изучить алгоритм покрытия с минимальной суммарной стоимостью.

2.3. Подготовить данные к эксперименту.

2.4. Провести вручную покрытие схемы по алгоритму.

 

 

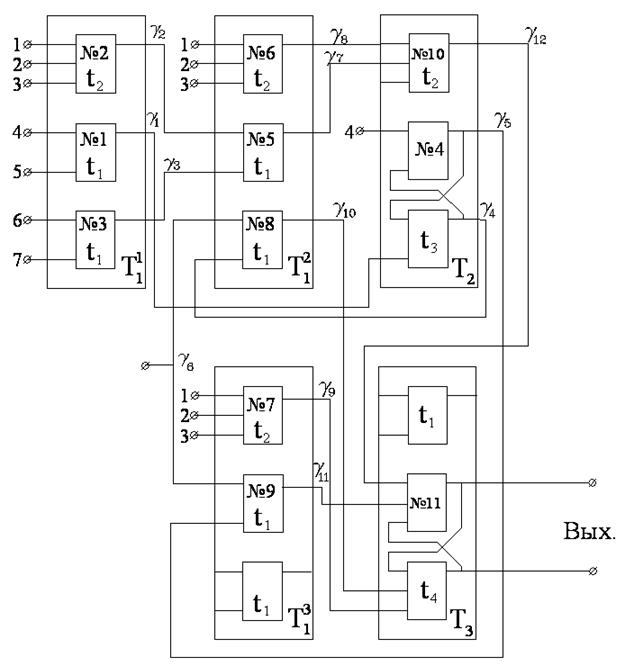
Рис. 1.4.

 

 

Рис. 1.5.