ЛАБОРАТОРНАЯ РАБОТА №1
ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АЛГОРИТМА ПОКРЫТИЯ СХЕМ МОДУЛЯМИ
Цель работы - исследовать эффективность алгоритма покрытия схем типовых модулей РЭС; усвоить особенности алгоритмизации и программирования задачи покрытия схем на ЭВМ; приобрести навык построения математических моделей объектов конструирования, реализации и исследования их при решении задачи покрытия в САПР.
ОБЩИЕ СВЕДЕНИЯ О ЗАДАЧЕ ПОКРЫТИЯ
Задача покрытия функциональной схемы типовыми модулями из заданного набора является задачей преобразования функциональной схемы в электрическую, т.е. схему соединения конструктивных элементов (резисторов, конденсаторов, транзисторов, интегральных схем, и т.д.) [1-3]. Решается эта задача одной из первых на этапе конструкторского проектирования. Поскольку при проектировании радиоэлектронных средств (РЭС) применяется большое многообразие электрорадиоэлементов (ЭРЭ), то наряду с задачей покрытия часто возникает необходимость определения оптимального набора этих элементов для каждого конкретного класса схемы, минимизация числа типов элементов набора в проектируемом устройстве.
Математическая формулировка задачи
Исходными данными для решения задачи покрытия являются: функциональная схема устройства и схемы типовых конструктивных элементов используемого набора модулей (интегральных схем, транзисторов, резисторов, конденсаторов, плат и т.д.).
Допустим, схема состоит из множества элементов E = {e1, e2,…,en} и для каждого из элементов 
известен тип функции F(ei) (i = 1, 2,…, l), которую он реализует (усилитель, детектор, триггер, схема «И», «ИЛИ» и т.д.).
Набор модулей определяется библиотекой T = {T1, T2,…, Tn}.
Количественный состав схемы по типам элементов опишем вектором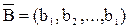 
, в котором bj – число элементов типа j. Состав модулей библиотеки опишем матрицей 
, в которой akj – число элементов типа j в модуле Tk. Отметим, что элемент схемы может быть реализован с помощью элемента того же типа, находящегося в одном из модулей библиотеки, либо с помощью элементов других типов. Например, элемент ИЛИ с двумя входами может быть реализован элементом ИЛИ с большим числом входов.
Схема считается покрытой модулями из библиотеки T, если каждый элемент схемы реализуется элементами, входящими в состав выбранных модулей.
В качестве критериев оптимальности в задаче покрытия используют:
- суммарную стоимость модулей, покрывающих схему;
- общее число модулей в покрытии;
- число типов используемых модулей;
- число связей между модулями;
- число неиспользованных элементов в модулях.
Ограничениями обычно являются требования на совместную или раздельную компоновку в едином конструктивном модуле элементов функциональной схемы, связанные с обеспечением нормального теплового режима, помехозащищенности и простоты диагностики.
Для оценки качества покрытия используют дополнительный критерий – коэффициент покрытия G = N/M, где N – число элементов в схеме, а M – число модулей (микросхем), которыми покрыта схема.
Рассмотрим наиболее распространенный вариант задачи, в котором критерием качества является суммарная стоимость модулей.
Пусть известны стоимости модулей каждого типа c1,…, ck,…, cm. Если ввести целочисленные переменные xk 
, определяющие число модулей типа k, которые необходимы для покрытия с минимальной стоимостью, задача сведется к минимизации функции
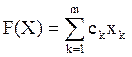(1.1)
при ограничениях
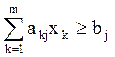, (1.2)
где j = 1, 2,…,l, a kj - число элементов типа j в T k.
Число логических функций любого типа k, входящих во все покрывающие модули, должно быть не меньше общего числа элементов соответствующего типа в реализуемой схеме.
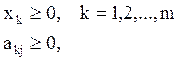(1.3)
xk – целое число для всех k, так как любой модуль используется только полностью, независимо от числа задействованных в нем компонентов.
Задача (1.1) – (1.3) является задачей целочисленного программирования.
Целевая функция для минимизации стоимости и числа модулей имеет вид:
,
где r1 и r2 – коэффициенты, учитывающие важность используемых критериев.
