Лабораторная работа № 2. 7.
Изучение явлений переноса в жидкостях
Цель работы: определение коэффициента динамической вязкости жидкости методом Стокса и его температурной зависимости.
I. Основные понятия и определения
Для изучения многих свойств жидкости, не связанных с потерями энергии направленного движения, достаточно модели идеальной жидкости, т. е. тела, не обладающего упругостью формы, несжимаемого, в объёме которого силы внутреннего трения (вязкости) не действуют. Тогда под это определение попадают не только собственно жидкости, но и газы в определённых условиях.
Применение модели идеальной жидкости позволяет изучить режимы течения жидкости: ламинарное и турбулентное, получить уравнение неразрывной струи υdS=const, уравнение Бернулли (ρυ2/2)+ρgh+p = const. Здесь υ - скорость течения жидкости, S – площадь поперечного сечения струи, ρ – плотность жидкости, h – высота столба жидкости, р – статистическое давление. Следует отметить, что так как все члены уравнения Бернулли имеют размерность давления, то ρgh называется гидростатическим давлением, ρυ2/2 – скоростным напором. Само уравнение Бернулли является законом сохранения энергии идеальной жидкости, где, соответственно, первый член – кинетическая энергия единицы объёма жидкости, второй – потенциальная энергия, третий – работа сил давления по его перемещению.
Учёт главного свойства реальной жидкости – вязкости, существенно нарушает уравнение Бернулли, так как часть механической энергии перемещения слоёв жидкости будет переходить во внутреннюю, тепловую энергию. Механизм внутреннего трения в жидкостях существенно отличается от того. Что происходит в газах (см. л. р. 5, 6). В жидкостях перемещению слоёв препятствуют силы взаимодействия между молекулами, которые линейно зависят от смещения только при малых смещениях молекул относительно положения равновесия. При смещении слоёв жидкости относительно друг друга смещения молекул велики и линейность нарушается, поэтому часть энергии направленного движения переходит во внутреннюю энергию жидкости – возникают силы внутреннего трения.
Несмотря на различный механизм внутреннего трения в жидкостях и газах макроскопическое уравнение для трения в жидкостях является уравнением Ньютона для внутреннего трения Fтр=-χ(dυ/dz), где χ – коэффициент динамической вязкости, (dυ/dz) – градиент скорости направленного движения. Наряду с коэффициентом динамической вязкости вводится понятие коэффициента кинематической вязкости.
Как и для газов, действие сил внутреннего трения устанавливает определённое распределение скоростей направленного движения по объёму жидкости. В случае покоящегося сосуда любое направленное перемещение в жидкости с течением времени прекратится.
С увеличением температуры энергия молекул жидкости увеличивается, и всё большее их число «покидает потенциальные ямы», жидкость разрыхляется, энергия взаимодействия молекул уменьшается, коэффициент вязкости уменьшается, следовательно, с ростом температуры коэффициент внутреннего трения уменьшается.
II. Методика эксперимента
Силы трения в жидкости определяются режимом её течения. При ламинарном течении сила трения пропорциональна скорости – закон Стокса. При турбулентном – квадрату скорости. Переход от ламинарного к турбулентному течению определяется числом Рейнольдса – безразмерной величиной, зависящей от вязкости жидкости, скорости её течения, формы тела или трубы. Если комбинация указанных величин меньше критического значения – течение ламинарное.
Рассмотрим падение шара в вязкой среде, считая режим обтекания его жидкостью ламинарным (метод Стокса). Тогда, согласно закону Стокса, на него действует сила внутреннего трения, тормозящая шар F=3πdυχ, где d – диаметр шара. Кроме того, на шар действует ускоряющая сила F, равная разности сил тяжести и архимедовой силы: F=πd3g (ρш – ρж)/6, где ρш, ρж - плотность материала шара и жидкости.
Если шар падает с некоторой высоты в жидкость, то он входит в жидкость с соответствующей начальной скоростью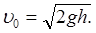 
Под действием ускоряющей силы шар продолжает двигаться в жидкости ускоренно, однако, ускорение уменьшается по мере роста скорости шара под действием силы внутреннего трения, пока не станет равным нулю. Следовательно, после прохождения в жидкости некоторого пути, шар начинает двигаться равномерно. Скорость равномерного движения Vp можно определить из формулы пути Vp= H/t,где Н – путь шара, пройденный равномерно за время t. Тогда из равенства F = Fтр, являющегося условием равномерного движения, получим для коэффициента внутреннего трения выражение вида:
χ=gd2t(ρш-ρж)/18H. (1)
Экспериментальная установка представляет собой подогреваемую трубу с исследуемой жидкостью и метками. Верхняя метка означает начало равномерного движения.
III. Проведение эксперимента и обработка результатов
- Отобрать для эксперимента четыре набора по три шарика разных диаметров. Определить их диаметр и плотность рш. Определить температуру жидкости.
- С некоторой высоты h бросать по очереди шарики одной серии время прохождения пути равномерного движения для каждого из них.
Результаты занести в таблицу.
t0=____0C, h=____м, ρш=___м3.
Таблица № 1.
| № п/п | d, м*10-3 | ρш | t, c | χ, Па*с | Χср, Па*с | δχср, Па*с | ηχ, % | А тр1, Дж | Атр2, Дж |
- По формуле (1) определить коэффициент динамической вязкости х и определить ошибку.
- На основе закона сохранения энергии определить работу сил трения на участке пути ускоренного движения (до верхней метки) Ат р1 и на участке равномерного движения (между метками) А т р 2 для одного из измерений.
- Повторить измерения по п.п. 1 - 4 для других температур после включения нагревателя.
- Построить график зависимости коэффициента внутреннего сгорания от температуры
Контрольные вопросы
- Какими свойствами обладает идеальная жидкость?
- Какие основные уравнения определяют течение идеальной жидкости?
- Какое влияние на течение жидкости оказывает её вязкость?
4. Каков механизм внутреннего трения в жидкостях? Чем отличается от механизма внутреннего трения в газах?
- Каким макроскопическим уравнением описывается вязкость жидкости?
- Как зависит сила внутреннего трения от вязкости жидкости?
- Почему коэффициент внутреннего трения зависит от температуры?
- Как движется тело в вязкой жидкости под действием силы тяжести?
- Как получить выражение для коэффициента динамической вязкости?
- Каков порядок определения коэффициента динамической вязкости методом Стокса?
- Как определить работу сил внутреннего трения при движении тела в жидкости?
