Цель работы: ознакомление со свойствами текущей идеальной жидкости на основе уравнения Бернулли.
Приборы и принадлежности: сосуд с водой, сосуд переменного сечения с вмонтированными в него коленами водяного манометра.
I. Основные понятия и определения.
Под идеальной понимают жидкость, которая несжимаема, и в которой отсутствует внутреннее трение. Графически течение жидкости представляют линиями тока. В каждой точке линии тока вектор скорости направлен по касательной к линии. Число линий через единичную перпендикулярную к линиям площадку равно значению скорости.
Замкнутая поверхность, образуемая линиями тока, называется трубкой тока, а жидкость в её объёме – струёй.
 |
Рассмотрим некоторую трубку тока переменного сечения (рис. 3.1).
За время dt через поперечное сечение S1 протекает масса жидкости 
и через сечение S2: -dm2= 
.
Вследствие несжимаеости dm1=dm2. Таким образом, 
т.е.
. (3.1)
для любого сечения жидкости. Это теорема о неразрывности струи.
Рассмотрим наклонную трубку тока (рис. 3.2), учитывая, что течение происходит под действием сил давления. Работа сил давления по пермещению массы dm в сечении 1: 
и в сечении 2: 
.
 |
Рис. 3.2.
Таким образом, полная работа: ΔА=dA2-dA1=(p2-p1)S 
dt. Но работа равна изменеию энергии текущей жидкости с обратным знаком. Таким образом, dA= -dE= -(dП+dК), где П и К потенциальная и кинетическая энергии: dП1=dmgh1, dK1= 
dП2=dmgh2, dK2= 
Подставив эти значения, получим: s dt(p2-p1)=-ΔE=dП1+dK1-dП2-dK2= 
dt[g(h2-h1)+ 
].
Группируя по индексам, получим 
= 
Так как сечения выбраны произвольно, то для каждого сечения:
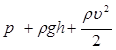=сonst. (3.2)
Это уравнение Бернулли и оно выражает закон сохранения энергии для единицы объёма текущей жидкости. В нём: p – статическое давление,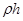 
- гидростатическое давление, 
- скоростной или динамический напор.
II. Методика эксперимента.
Наиболее распространённым методом измерения давления в текущей жидкости является метод трубок Пито (рис. 3.3).
 |
Запишем уравнение Бернулли для сечений 0, 1, 2.
0) 
=const;
1) 
=const, т. к.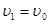 
приравняем уравнения и получим р1=р0, т.е. на входе первой трубки действует только статическое давление, уравновешиваемое столбом жидкости 
Для сечения 3: 
т.к. 
Давление на входе изогнутой трубки равно полному и урановешивается столбом жидкости h2, создающим давление 
, полное 
Исходя из теоремы неразрывности расход воды в единицу времени: 
и не зависит от сечения трубы. Из уравнения Бернулли для горизонтальной трубы:
,
получим:
,
h1 и h2 – высоты столба жидкости в трубках Пито. Так как V1=V2, то 
и 
Для предельного расхода воды получим:
=1-(
Так как 
окончательно:
(3.3)
Установка состоит из вертикальной стойки, закреплённой на основании. Внутри стойки горизонтально проходит полость различного сечения в разных её участках для протекания жидкости. Сверху в полости просверлены 4 канала с вставленными в них стеклянными трубками: две с донным отверстием и две с боковым отверстием. Или ещё используют изогнутую трубку для измерения статического давления в струе жидкости, протекающей в полости, и для определения скоростного напора. Для иллюстрации уравнения неразрывности струи каналы с трубками сделаны попарно в узкой и широкой частях полости. Через один из штуцеров, установленных на боковой стороне стойки, с помощью резиновой трубки поступает вода, а через другой — вода выливается в раковину.
III. Выполнение измерений и обработка результатов.
1. Определить время истечения обьёма V при различных перепадах давления.
Таблица № 3.1.
| № эксперимента | 
| 
| 
|
2. Определить расход воды в единицу времени по формулам:
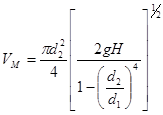, (3.4)
для каждого случая. Полученные результаты занести в таблицу № 3.1 и сравнить V и V0.
Контрольные вопросы.
1. Какую жидкость можно считать идеальной?
2. Что понимают под секундным массовым расходом жидкости?
3. Как получить уравнение неразрывности? В чём состоит его физический смысл?
4. Каковы особенности движения жидкости в струе при стационарном течении?
5. Как получить уравнение Бернулли?
6. Как применить уравнение Бернулли для жидкости, вытекающей из узкого отверстия в широком сосуде?
