II. Проведение эксперимента и обработка результатов

Лабораторная работа № 8.

Определение коэффициента внутреннего трения методом Стокса.

Цель работы: определение коэффициента внутреннего трения в глицерине методом Стокса.

Оборудование: прибор Стокса, стальные шарики, штангенциркуль, линейка, секундомер.

 

I. Основные понятия и определения.

1. Понятие о вязкости. При движении жидкости (под жидкостью можно понимать и газ) между её слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоёв. В газе возникновение этих сил объясняется тем, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество направленного движения, вследствие чего последний начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество направленного движения, что приводит к его торможению. В жидкости взаимодействие между слоями обусловлено взаимодействием между молекулами (межмолекулярные) взаимодействие. Поэтому потери на трение обусловлены затратами энергии на разрыв связей.

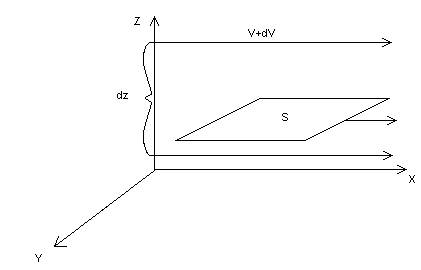
Рис. 8.1.

Рассмотрим жидкость, движущуюся в направлении оси х (см. рис. 8.1). Пусть слои жидкости движутся с разными скоростями. На оси z возьмём две точки, находящиеся на расстоянии dz. Скорости потока отличаются в этих точках на величину dV. Отношение dV/dz характеризует изменение скорости потока в направлении оси z и называется градиентом скорости.

Сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения и градиенту скорости:

. (8.1)

Величина «» называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Если в формуле (1) положить численно dV/dz =1 и S=1, то = f, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоёв, движущихся один относительно другого с градиентом скорости равным единице. В СИ размерность [ ] = кг*м^-1*с^-1. В системе СГС сила измеряется в длинах, поверхность в см², а градиент скорости имеет размерность 1/cек., тогда размерность будет [ ] = г*см^-1*с^-1. В системе СГС единица коэффициента вязкости называется пуазом. Часто пользуются меньшей единицей – сантипуазом: 1 сантипуаз=0,01 пуаз.

Коэффициент динамической вязкости зависит от природы жидкости и для данной жидкости с повышением температуры уменьшается. Вязкость играет существенную роль при движении жидкостей. Слои жидкости, непосредственно прилегающей к твёрдой поверхности, в результате прилипания остаётся неподвижным относительно неё. Скорость остальных слоёв возрастает по мере удаления от твёрдой поверхности. Наличие слоя жидкости между трущимися поверхностями твёрдых тел способствует уменьшению коэффициента трения. Наряду с коэффициентом динамической вязкости «» часто употребляют коэффициент кинематической вязкости:

.

В системе СГС единицей измерения коэффициента кинематической вязкости является 1 стокс: [ 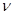] – см²/сек. В системе СИ: [ 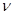] – м²/сек.

 

2. Метод Стокса. На движущийся в жидкости шарик действует сила внутреннего трения «f», тормозящая его движение. Эта сила по закону Стокса будет равна:

f =6 ,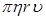

где r – радиус шарика, 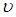- его скорость. Если шарик свободно падает в вязкой жидкости, то на него будут действовать сила тяжести P=mg= 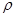Vg и выталкивающая сила P₁= Vg₁, равная весу жидкости в объёме шарика (V – объём шарика, 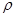- плотность шарика, - плотность жидкости).

На основании второго закона Ньютона имеем:

.

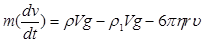Решением полученного уравнения является:

(8.2),

в чём можно убедиться непосредственной подстановкой. Поскольку с течением времени величина 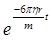очень быстро убывает, то скорость шарика вначале возрастает, но через малый промежуток времени становится величиной постоянной, равной:

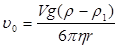. (8.3)

Здесь V= 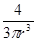– объём шарика.

Скорость шарика можно определить, зная расстояние «» между метками на сосуде и время «t», за которое шарик проходит это расстояние: 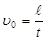. Тогда из выражения (8.3) следует, что коэффициент вязкости равен:

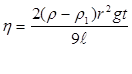. (8.4)

Формула (8.4) справедлива для шарика, падающего в безгранично простирающейся жидкости. Для нахождения измеряют t.

 

 

II. Проведение эксперимента и обработка результатов.

 

1. Определить плотность шарика.

На аналитических весах взвесить шарик (перед взвешиванием шарики должны быть тщательно очищены от глицерина). С помощью штангенциркуля измерить диаметр шарика. Используя полученные данные, определить плотность материала, из которого изготовлен шарик: где , m – масса шарика, d – диаметр шарика; 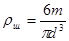, 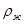=1,26*10³ кг/м³ (глицерин).

1. Измерить расстояние l от метки ‘1000” до метки “100”.
2. Пинцетом опустить шарик в цилиндр. Когда шарик окажется на уровне метки “1000”, пустить в ход секундомер, а в момент, когда шарик достигнет “100”, секундомер остановить.
3. Опыт повторить пять раз, начиная отсчёт секундомером каждый раз с более низкой отметки (например, с “шагом” 5 делений от отметки “1000”). Не следует делать расстояние слишком малым, чтобы не увеличивать погрешность измерений.
4. Все данные занести в таблицу.
5. Определить коэффициент внутреннего трения из каждого опыта и его среднее значение. Температура оказывает заметное влияние на коэффициент внутреннего трения, поэтому следует записать температуру, при которой производится опыт, а затем из таблицы взять плотность жидкости при данной температуре.

7. Вывести формулу для оценки погрешностей опытов.

1. Определить погрешность нахождения коэффициента вязкости по методу Стокса.
2. Результаты занести в таблицу 8.1.

Таблица 8.1.

N п/п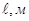
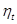
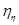
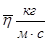
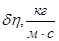
1.
2.
3.
4.

Контрольные вопросы.

1. Что такое вязкость? В каких единицах измеряется коэффициент вязкости?

2. Какие силы действуют на шарик, падающий в жидкости?

3. Почему, начиная с некоторого момента времени, шарик движется равномерно?

4. Как изменяется скорость движения шарика с увеличением его диаметра?

5. Нужно ли выводить поправочный коэффициент в формулу (4) в ваших измерениях?