Оценить границы доверительного интервала при косвенных измерениях чрезвычайно сложно, и в настоящее время не существует универсального способа определения этих границ для заданной надежности. Предлагается принять приближенную оценку погрешности косвенных измерений в соответствии с приведенной ниже литературой.
Если измеряемая физическая величина является функцией нескольких переменных
,
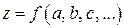то в этом случае нужно руководствоваться следующими правилами:
1. Для каждой серии измерений входящих величин необходимо провести обработку результатов, описанную в предыдущем параграфе, и получить значения доверительных интервалов
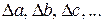
При этом для всех измеряемых величин задается одно и то же значение надежности 
.
2. Границы доверительного интервала для результата косвенных измерений могут быть определены по формуле:
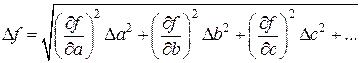
Здесь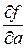 
, 
, 
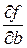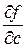,... - частные производные, которые вычисляются при средних значениях параметров:
, 
, 
,…
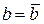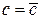(Частная производная функций многих переменных по одной переменной является обычной производной по этой переменной, если другие переменные при этом считаются постоянными.)
3. Окончательный результат записать в виде:
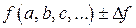
4. Определить относительную погрешность результата
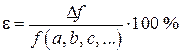
В заключение сделаем два замечания.
1. Если случайные погрешности результатов измерений меньше, чем погрешность измерительного прибора, то только погрешность прибора определит погрешность окончательного результата как прямых, так и косвенных измерений.
2. Необходимо помнить правила округления результатов. Например, если величина абсолютной погрешности составляет сотые доли, значит, мы ошибаемся в сотых долях, и нет смысла сохранять тысячные доли в результате.
Экспериментальная часть.
В данной работе предлагается провести многократные измерения периода колебания математического маятника (при постоянной амплитуде) с помощью электрического секундомера с ценой деления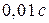 
, являющейся погрешностью 
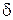секундомера.
Выполнение эксперимента.
1. Установить длину маятника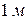 
.
2. Вывести маятник из положения равновесия, задав амплитуду, например,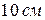 
.
3. Отпустить маятник, и после того, как будет совершено одно его полное колебание, измерить период одного следующего полного колебания. Для этого в момент прохождения маятником крайнего положения включить секундомер. При повторном прохождении этого же крайнего положения секундомер выключить.
4. Измерения, указанные в параграфе 3, провести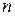 
раз, положив 
.
5. Полученные значения периодов занести в таблицу № 1.
6. Для построения гистограммы необходимо:
а) По горизонтальной оси отложить время, соответствующее полученным периодам колебаний, в масштабе 
, приняв за начало координат минимальное значение периода (см. Рис. 4.). По вертикальной оси отложить число появлений 
того или иного периода в масштабе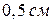 
- одно появление.
б) Обозначив минимальный период через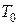 
, подсчитать общее число появлений четырех периодов: 
, 
, 
, 
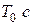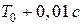. На отрезке 
построить прямоугольник с высотой, равной общему числу появлений этих четырех периодов.
в) Подсчитать общее число появлений следующих четырех периодов: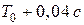 
, 
, 
, 
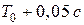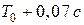. За основание соответствующего прямоугольника взять отрезок 
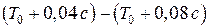. Высота прямоугольника должна быть равна соответствующему числу появлений периодов.
г) указанные построения проделать для всех периодов, полученных в эксперименте.
Таблица № 1.
| 
| 
| 
|
| . . . |
| 
|
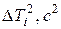
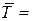
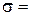
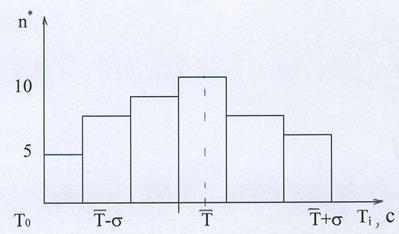
Рис. 4. Построение гистограммы.
7. Провести обработку результатов измерений в следующем порядке:
а) Вычислить среднее значение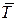 
из 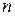измерений:
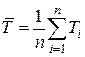
б) Вычислить погрешности отдельных измерений
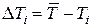
в) Вычислить квадраты погрешностей отдельных измерений
г) Определить среднюю квадратичную погрешность результата серии измерений:
д) Результаты, полученные в пунктах а, б, в, г, занести в таблицу № 1.
е) Найти в справочной таблице коэффициент Стьюдента 
для надежности 
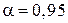и числа проведенных измерений .
ж) Определить полуширину доверительного интервала:
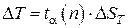
з) Окончательный результат записать в виде:
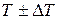
и) Оценить относительную погрешность результата серии измерений
8. На оси периодов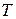 
отметить среднее арифметическое значение 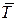, величину 
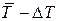и 
. При достаточно большом числе измерений в интервал 
должно попадать наибольшее число значений полученных периодов.
9. Для точных измерений периода колебаний маятника обычно используют метод, при котором измеряется время 
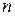большего числа колебаний. Положив , найти период колебаний по формуле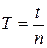 
и сравнить этот результат со значением 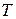в п. 7а.
Контрольные вопросы.
1. Что называется доверительным интервалом и надежностью?
2. Что такое средняя квадратичная погрешность?
3. Что такое дисперсия распределения?
4. В каком случае дисперсия распределения равна квадрату средней квадратичной погрешности?
5. Зависит ли точность измерения периода колебания маятника методом, использованным в п.9 от величины начальной амплитуды?
Приложение.
Для большинства технических измерений ГОСТ (государственный стандарт) или ведомственные правила (ОСТ) устанавливают надежность измерений 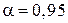. Поэтому и в нашем практикуме вы будете все результаты приводить с надежностью 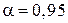. При этом для нашего физического практикума из таблицы Стьюдента потребуется только следующая строчка:
|
| … | … | |||||||
|
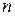
| 12,7 | 4,3 | 3,2 | 2,8 | 2,7 | 2,2 |
Литература.
1. О.Н. Кассандрова, В.В. Лебедев. «Обработка результатов наблюдений». М., «Наука», 1970.
2. А.Н. Зайдель. «Элементарные оценки измерений». М., «Наука», 1968.
3. И.С. Роменко. «Руководство по вычислению ошибок измерений». М., изд. МИФИ, 1969.
4. Савельев И.В. «Курс общей физики в пяти книгах». М., АСТРЕЛЬ, А.С.Т., 2003.
