Цепь переменного тока с емкостным элементом

На рис. 8 приведена схема цепи переменного тока с емкостным элементом (конденсатором).

Рис. 8.

Под действием синусоидального напряжения u = U_m sin ωt в цепи с емкостным элементом протекает ток

(19)

где С – емкость; q – заряд на электродах емкостного элемента.

Из выражения (19) видно, что в цепи с емкостным элементом ток опережает по фазе напряжение на угол 90º (π/2) (см. рис. 8).

В цепи переменного тока емкостный элемент обладает сопротивлением, которое называется емкостным и обозначается Х_С.

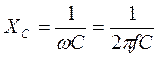(20)

В системе СИ сопротивление X_C измеряется в омах (Ом).

Математическое выражение закона Ома для этой цепи

(21)

Мгновенная мощность в цепи с емкостным сопротивлением будет в противофазе с мгновенной мощностью в цепи с индуктивным элементом

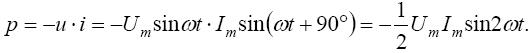
(22)

Анализ приведенных формул показывает, что в цепи с емкостью (как и в цепи с индуктивностью) мощность в первую четверть периода забирается из сети и запасается в электрическом поле конденсатора, а в следующую четверть периода возвращается в сеть. Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность

Q_С=I²X_С.

(23)

Энергия, запасаемая в электрическом поле конденсатора,

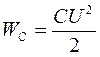(24)

Анализ неразветвленной цепи переменного тока

Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений (рис. 9).

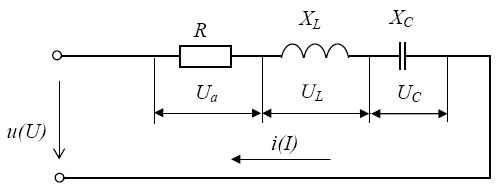
Рис. 9.

При прохождении тока в цепи на каждом элементе возникает падение напряжения:

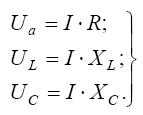
(25)

Для каждого элемента цепи угол сдвига по фазе между током и напряжением имеет свое значение. Вектор приложенного к схеме напряжения U определится как сумма векторов напряжений на отдельных элементах схемы. Для рассматриваемой одноконтурной схемы в соответствии со вторым законом Кирхгофа справедливо уравнение

(26)

Для анализа работы данной цепи построим векторную диаграмму (рис. 10). Перед построением выбирается масштаб для тока и напряжения. Построение векторной диаграммы начинают с вектора той величины, которая является общей для всех элементов цепи. В данном случае при последовательном соединении общей величиной для всех элементов цепи является ток. Поэтому первым проводим вектор тока. Вектор напряжения на активном сопротивлении совпадает по фазе с вектором тока. Вектор напряжения на индуктивном сопротивлении опережает вектор тока на угол 90º, а вектор напряжения на емкостном сопротивлении отстает от вектора тока на угол 90º.

Рис. 10.

Знак перед углом сдвига фаз φ зависит от режима цепи. Если в рассматриваемой цепи преобладает индуктивное сопротивление, то

U_L>U_C.

(27)

В этом случае нагрузка имеет активно-индуктивный характер, а напряжение U опережает по фазе ток I (угол φ положительный).

Если в цепи преобладает емкостное сопротивление, то

U_L<U_C.

(28)

В этом случае нагрузка имеет активно-емкостный характер, а напряжение U отстает по фазе от тока I (угол φ отрицательный).

Выделим из векторной диаграммы треугольник напряжений (рис. 11), из которого следует:

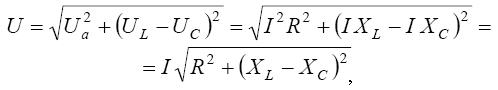
(29)

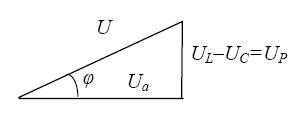Рис. 11.

Закон Ома для неразветвленной цепи запишется в виде

(30)

где Z – полное сопротивление неразветвленной цепи,

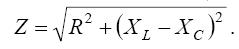
(31)

Если стороны треугольника напряжений разделить на силу тока, получится треугольник сопротивлений; если стороны треугольника напряжений умножить на силу тока, получится треугольник мощностей (рис. 12).

Рис. 12.

Из приведенных треугольников можно записать уравнения, которые широко используются при анализе электрических цепей.

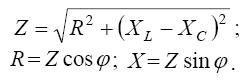
(32)

Из треугольника мощностей:

(33)

где S – полная мощность; Р – активная мощность; Q – реактивная мощность;

S=UI.

(34)

Размерность полной мощности – вольт-ампер (ВА); размерность активной мощности – ватт (Вт); размерность реактивной мощности – вольт-ампер реактивный (ВАр).

Величина cos φ называется коэффициентом мощности цепи.

	(35)
	(36)

Полное сопротивление может быть представлено комплексным числом в алгебраической и показательной форме. Комплекс полного сопротивления в алгебраической форме

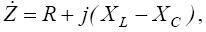
(37)

где j – мнимая единица (j ²= − 1).

Комплекс полного сопротивления в показательной форме

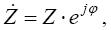
(38)

Где

Резонанс напряжений

В замкнутом контуре электрической цепи (см. рис. 9), содержащей активное сопротивление R, индуктивность L и емкость С, при условии равенства реактивных сопротивлений

X_L = X_C

(39)

возникает резонанс напряжений.

Выразим X_L и X_C через частоту ω и подставим в равенство (39)

(40)

Откуда

(41)

где ω_рез – частота питающего напряжения; ω ₀ – частота собственных колебаний LC -контура.

Резонанс напряжений возникает в том случае, когда частота питающего напряжения равна частоте собственных колебаний LC -контура.

Следовательно, добиться резонанса напряжений можно изменением частоты ω_рез или параметров контура L и C.

При резонансе напряжений

(42)

т.е. полное сопротивление цепи становится минимальным и равным только активному сопротивлению. Следовательно, ток при резонансе напряжений максимальный.

Рис. 13.

При резонансе напряжений (рис. 13)

U_L=U_C.

(43)

Если при этом

X_L=X_C>R,

(44)

то напряжение на участке с индуктивным сопротивлением и равное ему напряжение на участке с емкостным сопротивлением будут больше питающего напряжения U.

Из векторной диаграммы (см. рис. 13) видно, что при резонансе напряжение U, приложенное к цепи, оказывается равным напряжению на активном сопротивлении (U=U_а) и совпадает по фазе с током I, т.е. угол сдвига фаз между I и U равен нулю (φ =0).

Выполнение работы.

Работа выполняется с использованием стенда, схема которого изображена на рис 14. Коммутация элементов производится с помощью тумблеров и перемычек. Возможна установка двух значений индуктивности L (одна или две последовательно включенные индуктивные катушки) и любого значения электроемкости С в интервале от 0 до 15,75 мкФ с шагом 0,25 мкФ. Это позволяет получить любой нужный режим в цепи.

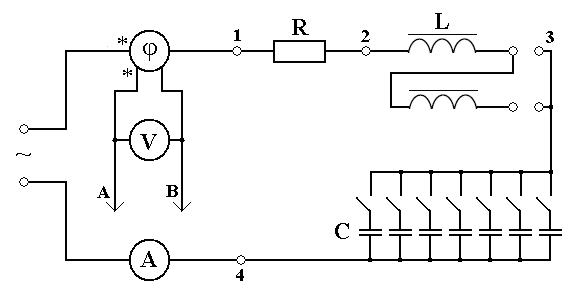
Рис. 14.

Параметры каждого элемента и цепи в целом измеряются на данном участке с помощью вольтметра, амперметра и фазометра. Щупы «А» и «В» подключаются к соответствующим клеммам (1, 2, 3, 4), причем щуп «А» должен подключаться к клемме с меньшим номером, чтобы фазометр давал верные показания.

Индуктивный режим последовательной цепи экспериментально определяется по φ > 0 для цепи в целом. Рекомендуется установить φ > 30°.

Емкостный режим характеризуется φ < 0. Рекомендуется при измерениях установить φ < -30°.

При резонансном режиме φ = 0.

Задание.

1. Установите индуктивный режим последовательной цепи, изменяя величины L и C. Измерьте I, U и φ для каждого элемента и цепи в целом. Результаты занесите в таблицу 1. По полученным данным рассчитайте Z, R, X, U_a, U_p, S, P, Q. Постройте векторную диаграмму для силы тока I и напряжений U, U_R, U_L, U_C в соответствии с результатами эксперимента.

2. Установите емкостный режим цепи и исследуйте ее аналогично п. 1, занеся данные в таблицу 2. Постройте векторную диаграмму.

3. Установите резонансный режим цепи и исследуйте ее аналогично п. 1, занеся данные в таблицу 3. Постройте векторную диаграмму.

Таблицы 1, 2, 3,

Режим - …
Участок Величины	Вся цепь (1 – 4)	R (1 – 2)	L (2 – 3)	C (3 – 4)
U, В
I, A
φ, гр
Z, Ом
R, Ом
X, Ом
U _a, В
U _p, В
S, ВА
P, Вт
Q, ВАр