Лабораторная работа № 13.
Цель работы: определение видов сухого внешнего трения и их коэффициентов при скатывании шара по наклонной плоскости.
I. Основные понятия и определения.
Из опыта известно, что полная механическая энергия движущегося тела в реальной ситуации с течением времени уменьшается. Причина уменьшения — действие сил трения, проводящих энергию направленного движения во внутреннюю, тепловую энергию трущихся тел.
В зависимости от состояния взаимного движения соприкасающихся тел различают трение покоя, трение скольжения и трение качения (скатывания).Так как величина деформации поверхности определяется давлением тел друг на друга, то и сила трения должна быть пропорциональна давлению. Для не очень значительных деформаций справедлив закон Амонтона-Кулона:
Fтр=kFд, (13.1)
где Fтр, Fд — силы трения и давления. Безразмерный коэффициент трения k определяется видом трения: наибольший для трения покоя, меньше для трения скольжения и незначителен для трения качения.
Кроме того, при трении качения деформация зависит от радиуса тела при неизменной массе и поэтому при качении k=δ/R, где δ – плечо силы трения, R – радиус катящегося тела. Наиболее сложная картина трения наблюдается при качении круглого тела по плоскости.
На рис.13.1 а) приведён примерный вид деформации, создаваемой катящимся телом. Очевидно, что деформация х1 является упругой и на движение тела не влияет. Эта причина трения сцепления аналогична трению покоя. Деформация х2 является пластической. Именно она, как показано на рис.13.1 б), препятствует движению тела. Сила сопротивления движению F следует разложить на две составляющие. Тогда N – реакция опоры и уравновешивает давление тел на плоскость, Fk – cила трения качения. Силы N и Fk создают моменты сил относительно точки О. Учитывая, что δ<<R (точки А и А’ почти совпадают), можно считать плечом силы Fk величину R, плечом силы N величину δ. Тогда уравнение вращательного движения тела будет иметь вид:
I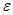 
=FkR-Nδ. (13.2)
Рис. 13.1.
Деформация поверхности при качении круглого тела, где I – момент инерции тела, ε– угловое ускорение. Если тело движется под действием некоторой силы F1, то поступательное движение центра О будет описываться уравнением:
ma=F1-Fk. (13.3)
При рассмотрении движения тела предполагалось, что линейные скорости центра инерции тела О и точек поверхности совпадают (V=ωR). В противном случае, например, тело отпускается на плоскость, обладая начальной линейной или угловой скоростями, начинается проскальзывание поверхности тела относительно плоскости. Возникает трение скольжения, которое замедляет или ускоряет качение тела по плоскости.
Поместим шар в направляющий желоб прямоугольного сечения, наклонённый к горизонту под углом α. Как следует из рис. 13.2 ситуация в сравнении с рис. 13.1 отличается только точкой приложения сил сопротивления движению, поэтому плечо приложения сил N и Fk будет r. Решая уравнения (13.2) и (13.3) совместно, получим для ускорения движения центра инерции шара в желобе выражение:
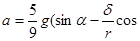α).
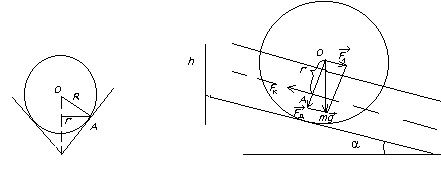
Рис. 13.2.
Если угол α мал, то sinα≈α(рад.), cosα≈1 и выражение для ускорения примет вид:
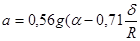). (13.4)
Из выражения (13.4) следует, что при отсутствии трения, шар имел бы ускорение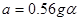 
. К аналогичному результату можно прийти, рассмотрев закон сохранения энергии для катящегося тела. Согласно ему потенциальная энергия в начале желоба mgh переходит в кинетическую энергию поступательного mV2/2 и вращательного Iω2/2 движения, 2mgh=mV2+Iω2, V=ωR0.71.
Действие сил трения уменьшает энергию шара, что приводит к уменьшению ускорения шара, согласно выражению (13.4). Если бы шар сходил с желоба без качения (скользил), то вся потенциальная энергия перешла бы в кинетическую энергию поступательного движения, и ускорение было бы равным gα., т.е. больше, чем при наличии вращательного движения. Следовательно, если шар при качении будет проскальзывать, то его ускорение будет больше 0,56g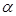 
.
II. Описание эксперимента.
Изучение действия сил трения при качении шара проводится на установке, представляющей из себя желоб прямоугольного сечения с регулируемым углом наклона относительно горизонта. Шар в верхнем положении удерживается электромагнитом. Время отсчитывается по электронному секундомеру. Измерение автоматизировано. Пуск производится тумблером “ Пуск”.
После прохождения шаром желоба секундомер автоматически останавливается. Установка готова к следующему измерению при приведении тумблера ”Пуск ” в исходное положение и сброса показаний секундомера.
При известной длине желоба l, ускорение движения шара определяется из формулы пути равноускоренного движения 
. Если построить график в координатах а (м/с2)-α(град), то он будет иметь вид примерно такой же, как и на графике, рис. 13.3. Здесь прямая а т - ускорение катящегося без трения шара, a =0,56g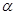 
.
 |
Кривая а э - экспериментальная зависимость ускорения шара, определенная из выражения
, где t- время, определенное экспериментально. Очевидно, что при малых α < α0 действует сила трения покоя, и шар будет покоиться до пересечения пунктирного продолжения экспериментальной кривой с осью α. Затем, при α >α0 шар начинает катиться, и действует сила трения качения для углов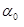 
< < 
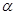. Угол 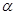, определяется пересечением продолжения экспериментальной кривой с теоретической. При углах 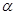> , центр шара движется настолько быстро, что он начинает проскальзывать, т. е. ускорение его возрастает за счёт увеличения доли поступательного движения.
Рис. 13.3.
