Определение 54. Функцию 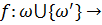 {классы Фиттинга групп} называют
{классы Фиттинга групп} называют  - радикальной функцией простого натурального аргумента или, коротко,
- радикальной функцией простого натурального аргумента или, коротко,  -функцией. Функцию
-функцией. Функцию  {классы Фиттинга групп}называют радикальной функцией простого натурального аргумента или, коротко,
{классы Фиттинга групп}называют радикальной функцией простого натурального аргумента или, коротко,  -функцией.
-функцией.
Лемма 10. Пусть  –
– 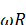 – функция,
– функция,  -
-  -функция и
-функция и 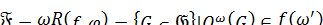 и
и  для всех
для всех  }. Тогда
}. Тогда  является классом Фиттинга.
является классом Фиттинга.
Определение 55. Класс Фиттинга  называют -веерным, если
называют -веерным, если  , где
, где  и
и  - некоторые
- некоторые 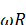 -функция и
-функция и  -функция соответственно. Функцию
-функция соответственно. Функцию  называют -спутником, а функцию
называют -спутником, а функцию  -направлением
-направлением  -веерного класса Фиттинга
-веерного класса Фиттинга  . Пусть
. Пусть  -
-  -функция. Класс Фиттинга
-функция. Класс Фиттинга  называется веерным, а
называется веерным, а  называется
называется  -спутником веерного класса Фиттинга
-спутником веерного класса Фиттинга  .
.
Лемма 11. Пусть  группа минимального порядка из
группа минимального порядка из  , где
, где 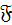 и
и  классы Фиттинга. Следовательно,
классы Фиттинга. Следовательно, 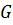 комонолитична с комонолитом
комонолитична с комонолитом  .
.
Лемма 12. Пусть -класс Фиттинга и  . Тогда
. Тогда  , где
, где  -
-  -функция такая, что
-функция такая, что  ,
,  для всех
для всех 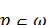 и
и  -произвольная
-произвольная  -функция. В частности, классы Фиттинга
-функция. В частности, классы Фиттинга  и (1) являются
и (1) являются  -веерными для любого непустого множества
-веерными для любого непустого множества  .
.
Доказательство.
Пусть  , где
, где  и
и  – из условия леммы. Покажем, что
– из условия леммы. Покажем, что  . Пусть
. Пусть  . Тогда
. Тогда  и из
и из  следует, что
следует, что  . Таким образом,
. Таким образом,  и, значит,
и, значит,  .
.
Предположим, что  и -группа наименьшего порядка из
и -группа наименьшего порядка из  . Тогда
. Тогда 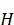 является комонолитической группой с комонолитом
является комонолитической группой с комонолитом  . Поскольку
. Поскольку  , то
, то  и
и  . Пусть
. Пусть  . Тогда
. Тогда  и
и  , что невозможно. Следовательно
, что невозможно. Следовательно  . Лемма доказана.
. Лемма доказана.
Лемма 13. Пусть  , где -произвольная
, где -произвольная  -функция. Тогда справедливы следующие утверждения:
-функция. Тогда справедливы следующие утверждения:
1)  , где
, где  для любого
для любого  ;
;
2)  , где
, где  и
и  для всех
для всех 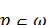 ;
;
3) если  и
и  , то
, то  и
и  для всех
для всех  .
.
Доказательство:
1) Пусть  , где
, где  -
-  -функция из условия леммы. Покажем, что
-функция из условия леммы. Покажем, что 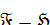 . Так как
. Так как  для любого
для любого  , то
, то  . Пусть
. Пусть  . Тогда по определению классов Фиттинга,
. Тогда по определению классов Фиттинга,  и
и  для любого
для любого  . Так как
. Так как 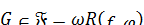 , то
, то  и
и  для любого
для любого  , следовательно
, следовательно  и
и  для любого
для любого  . По определению -веерного класса Фиттинга заключаем, что
. По определению -веерного класса Фиттинга заключаем, что  . Таким образом,
. Таким образом,  . Тем самым мы показали, что
. Тем самым мы показали, что 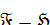 .
.
2) Пусть 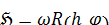 , где
, где  - из условия леммы. Покажем, что
- из условия леммы. Покажем, что 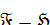 . Пусть
. Пусть  . Тогда
. Тогда  и
и  для любого
для любого  и, кроме того,
и, кроме того,  . Таким образом
. Таким образом  и
и  для любого
для любого  . Следовательно, по определению -веерного класса Фиттинга, имеем
. Следовательно, по определению -веерного класса Фиттинга, имеем  . Значит
. Значит  . Допустим, что
. Допустим, что  . Пусть
. Пусть  ,
, 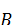 -группа минимального порядка с таким свойством. Тогда, по лемме Ц,
-группа минимального порядка с таким свойством. Тогда, по лемме Ц, 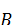 комонолитична с комонолитом
комонолитична с комонолитом  . Допустим, что
. Допустим, что  . Тогда, так как
. Тогда, так как  , то
, то  . Противоречие. Значит,
. Противоречие. Значит, 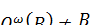 и
и  . Поэтому
. Поэтому  и из
и из  . Следовательно,
. Следовательно,  . Поэтому
. Поэтому  . Так как
. Так как  , то есть
, то есть 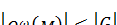 и
и  , то
, то  . Далее, из
. Далее, из  следует, что
следует, что  для любого
для любого  . Таким образом, по определению -веерного класса Фиттинга, заключаем, что
. Таким образом, по определению -веерного класса Фиттинга, заключаем, что  . Противоречие. Следовательно, допущение не верно и
. Противоречие. Следовательно, допущение не верно и 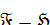 .
.
3) Пусть  и
и  . Так как
. Так как  (по условию), то существует
(по условию), то существует  . Поэтому
. Поэтому  и, значит,
и, значит,  . Из
. Из  (так как
(так как  ). А получаем, что
). А получаем, что  следовательно
следовательно  для любого
для любого 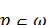 .
.
Определение 56. Направление  -веерного класса Фиттинга назовают:
-веерного класса Фиттинга назовают:
 -направлением, если
-направлением, если  для любого
для любого  ;
;
 -направлением, если
-направлением, если  для любого
для любого  ;
;
 -направлением, если
-направлением, если  для любого
для любого  ;
;
 -направлением, если формация Фиттинга
-направлением, если формация Фиттинга  -разрешима для любого
-разрешима для любого  .
.
Пусть  – множество направлений -веерного класса Фиттинга
– множество направлений -веерного класса Фиттинга  .
.  -функцию
-функцию  называют
называют  -направлением
-направлением  -веерного класса Фиттинга
-веерного класса Фиттинга  , если
, если  является
является 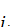 -направлением для любого
-направлением для любого  . Направление
. Направление 
 -расслоенного класса Фиттинга называется
-расслоенного класса Фиттинга называется  -направлением
-направлением 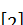 , если
, если  для любой неабелевой группы
для любой неабелевой группы  .
.
Лемма 14. Пусть  с -направлением
с -направлением  и
и  . Тогда
. Тогда
1) Если 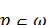 ,
,  и
и  , то
, то  .
.
2) Если  и
и 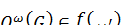 , то
, то  .
.
3) Если  ,
,  для любого
для любого 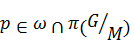 и
и 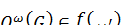 , то
, то  .
.
Доказательство:
1) Так как  и
и  , то
, то  . По условию
. По условию  . Пусть
. Пусть  . Тогда
. Тогда 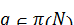 . Поскольку
. Поскольку  является -направлением, то
является -направлением, то  и по лемме 1, п.9 получим
и по лемме 1, п.9 получим 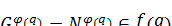 и, значит, по определению
и, значит, по определению  , имеем
, имеем  .
.
2) По условию  и
и  . Пусть
. Пусть  . Так как
. Так как  является
является  - группой и
- группой и  является
является  – направлением, то по лемме 1, п.9 имеем
– направлением, то по лемме 1, п.9 имеем  для всех
для всех  . По определению
. По определению  имеем
имеем  .
.
3) По условию  и
и  для любого
для любого  . Пусть
. Пусть  . Тогда
. Тогда  является
является 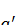 - группой. Так как
- группой. Так как  является -направлением, то по лемме 1, п.9 получим
является -направлением, то по лемме 1, п.9 получим  . Следовательно.
. Следовательно.  для всех
для всех  и, значит, по определению
и, значит, по определению  , имеем
, имеем  . Лемма доказана.
. Лемма доказана.
3.2 Произведение  -веерных классов Фиттинга.
-веерных классов Фиттинга.
Лемма 15. Пусть  и
и  -
-  -классы Фиттинга с -направлением
-классы Фиттинга с -направлением  ,
,  и
и  - внутренние
- внутренние  -спутники
-спутники  и
и  соответственно. Если
соответственно. Если  с -спутником
с -спутником  таким, что
таким, что  ,
,  для всех
для всех  и
и  для всех
для всех  , то
, то  и
и  является внутренним
является внутренним  -спутником класса Фиттинга
-спутником класса Фиттинга 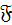 .
.
Доказательство:
Пусть  . Допустим, что
. Допустим, что 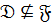 . Пусть
. Пусть  и группа
и группа 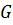 наименьшего порядка с таким свойством. Тогда
наименьшего порядка с таким свойством. Тогда 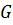 – комонолитическая группа с комонолитом
– комонолитическая группа с комонолитом  . Из
. Из 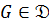 следует, что
следует, что  . Допустим, что
. Допустим, что  является
является  - группой. Тогда
- группой. Тогда  и по лемме 14 п. 2)
и по лемме 14 п. 2)  , что невозможно. Следовательно,
, что невозможно. Следовательно,  -
-  -группа. Из
-группа. Из  следует, что
следует, что  .
.
Пусть  . Тогда
. Тогда  для всех
для всех  и
и  для всех
для всех  . Следовательно,
. Следовательно,  . Получили противоречие.
. Получили противоречие.
Пусть  . Тогда
. Тогда 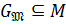 ,
, 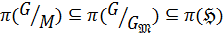 и
и  . Отсюда следует, что
. Отсюда следует, что  для любого
для любого  . Тогда по лемме 14 п. 3) имеем
. Тогда по лемме 14 п. 3) имеем  . Получили противоречие. Лемма доказана.
. Получили противоречие. Лемма доказана.
Теорема 13. Пусть  и
и  -
-  -классы Фиттинга с внутренними -спутниками
-классы Фиттинга с внутренними -спутниками  и
и  соответственно и с
соответственно и с  -направлением
-направлением  таким, что
таким, что  . Тогда
. Тогда  является
является  -веерным классом Фиттинга с направлением
-веерным классом Фиттинга с направлением  и с внутренним
и с внутренним  -спутником
-спутником  таким, что
таким, что  ,
,  для всех
для всех  и
и  для всех
для всех  .
.
Доказательство:
Пусть  . Пусть
. Пусть  , причем
, причем  ,
,  для любого
для любого  ,
,  для всех
для всех  . Покажем что
. Покажем что  .
.
а) Покажем, что  . Так как
. Так как  ,
, 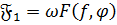 , следовательно,
, следовательно,  , следовательно,
, следовательно, 
б) Допустим, что  . Пусть
. Пусть  ,
, 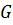 -группа наименьшего порядка с таким свойством. Тогда по
-группа наименьшего порядка с таким свойством. Тогда по лемме Ц* 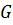 комонолитична с комонолитом
комонолитична с комонолитом  . Так как
. Так как  , то
, то  , для всех
, для всех  ,
,  . Так как
. Так как 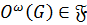 ,
,  , то
, то  (по определению -радикала группы
(по определению -радикала группы 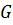 ). Пусть
). Пусть  . Тогда
. Тогда  , следовательно,
, следовательно,  . По условию,
. По условию,  , следовательно,
, следовательно,  для всех
для всех  , следовательно,
, следовательно,  . По
. По лемме *  . Так как группа
. Так как группа 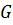 комонолитична, то
комонолитична, то  и, значит,
и, значит,  . Поэтому
. Поэтому 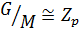 . Из
. Из  и
и  следует, что
следует, что  и, значит,
и, значит,  . Поэтому
. Поэтому 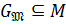 и
и  . Из
. Из  следует, что
следует, что  . Допустим, что
. Допустим, что  . Тогда
. Тогда 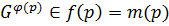 . Так как
. Так как  , то по лемме 14 п. 1)
, то по лемме 14 п. 1)  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  . Из
. Из  следует, что
следует, что  . Тогда для любого
. Тогда для любого  имеем
имеем  и, значит,
и, значит, 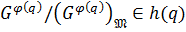 . Поэтому
. Поэтому  для любого
для любого  . В силу
. В силу леммы 10 можем считать, что  . Из
. Из  , следует, что
, следует, что  . Тогда
. Тогда  ,
,  и, значит,
и, значит,  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  . Теорема доказана.
. Теорема доказана.
Следствие 2. Пусть  и
и  -
-  -полные классы Фиттинга с внутренними -спутниками
-полные классы Фиттинга с внутренними -спутниками  и
и  соответственно. Тогда
соответственно. Тогда  является -полным классом Фиттинга с внутренним
является -полным классом Фиттинга с внутренним  -спутником
-спутником  таким, что
таким, что  ,
,  для всех
для всех  и
и  для всех
для всех  .
.
Следствие 3. Пусть  и
и  -
-  -локальные классы Фиттинга с внутренними -спутниками
-локальные классы Фиттинга с внутренними -спутниками  и
и  соответственно. Тогда
соответственно. Тогда  является -локальным классом Фиттинга с внутренним
является -локальным классом Фиттинга с внутренним  -спутником
-спутником  таким, что
таким, что  ,
,  для всех
для всех  и
и  для всех
для всех  .
.






