Пример. Вычислить приближенное значение интеграла
Точное значение:
Задание 1. Вычислить интеграл 
по формулам левых и правых прямоугольников, разделив интервал интегрирования на 5 равных частей (n=5).
· Введем значения n=5, a=0, b=1 в ячейки B5, B6, D6 соответственно.
· Шаг интегрирования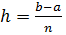 
вычислим в ячейке F6 по формуле = (D6-B6)/B5.
· Введем номера узлов интегрирования в ячейки A10:A15.
· Вычислим значения узлов интегрирования x0, x1, x2,x3, x4, x5: в ячейку B10 введем формулу =В6 в ячейку В11 введем формулу =В10+$F$6 скопируем ее до строки 15.
· Вычислим значения подынтегральной функции в интегрирования: ячейку С10 введем формулу =3*В10*В10-4*В10 скопируем ее до строки 15.
· Вычислим приближенное значение интеграла по формулам левых и правых прямоугольников в ячейке Е17 =F6*СУММ (С10:С14)
в ячейке Е18 = F6*CУММ (С11:С15)
Задание 2. Вычислить интеграл по формуле средних прямоугольников и формуле трапеций, разделив интервал интегрирования на 5 равных частей (n=5).
· Вычислим значение x между узлами интегрирования по формулам (xi-1+xi)/2 в ячейках E10:E14 в ячейку E10 введем формулу =(В10+В11)/2 и скопируем до строки E14.
· Вычислим в ячейках F10:F14 значения подынтегральной функции для аргументов в ячейках F10:F14.
· Вычислим приближенное значение интеграла по формулам средних прямоугольников в ячейке Е19 =F6*CУММ(C11:С14.
и трапецией в ячейке Е20 =F6/2*(С10+С15+2*СУММ(С11:С14).
Задание 3. Найти приближенное значение интеграла по формулам левых и правых прямоугольников, трапеций и Симпсона, разделив интервал интегрирования на 10 равных частей (n=10).
1) Вычислим новый шаг интегрирования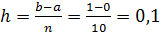 
т.е. шаг уменьшается в два раза. Значения новых узлов интегрирования будут x0=0, x1=0,1 x2=0,3…x9=0,9 x10=1
Заметим, что при решении задания 2 были вычислены все недостающие (нечетные) узлы интегрирования и соответствующие им значения подынтегральной функции: ячейки В10:В15 и С10:С15 содержат четные узлы интегрирования и соответствующие им значения подынтегральной функции, а ячейки Е10:Е14 и F10:F14 содержат нечетные узлы интегрирования и соответствующие им значения подынтегральной функции.
2) Изменить нумерацию узлов интегрирования в А10:Ф15 на четную, а в ячейках D10:D14 ввести нечетную нумерацию.
3) Самостоятельно вычислить интеграла по формулам левых и правых прямоугольников,трапеций. Обратить внимание, шаг интегрирования в ячейке F6 необходимо поделить на 2.
4) Вычислим приближенное значение интеграла по формуле Симпсона в ячейке F21 =F6/6*(C10+C15+4*СУММ(E10:E14)+2*СУММ(С11:С14))
Лабораторная работа 4
Решение дифференциальных уравнений методом Эйлера
1. Цель работы
Изучение метода Эйлера для интегрирования дифференциальных уравнений.
