Задание 1. Отделение корней уравнения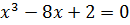 
на отрезке [-3;3].
Для отделения корней можно построить график функции y=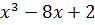 
, задав шаг изменения аргумента, например, равным 1. График удобно строить, используя Мастер диаграмм.
Построение графика в Open Office.org Calc
1)мастер диаграмм;линии;далее
2)диапазон; данных; ввести числовые значения B3:H3;
переключатель: ряды данных в строке; далее
3)категории: ввести числовые значения B2:H2 далее
4)отображение сетки оси x; готово
5)ПК; правка: ось x; свойства объекта; линии: цвет синий; толщина
:0,1:
Графика функции с осью x
Значениями действительных корней уравнения являются точки пересечения графика функции с осью x. Из графика видно, что корни находятся на интервалах [-3;-2],[ 0;1] и [2;3].
Задание 2. Определение начального приближения x0.
1. Найдем производные левой части уравнения f(x)=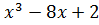 
f’(x)=3x2-8,
f”(x)=6x.
2. Проверим условие сохранения знаков производных на отрезке [-3;-2].
Первая производная меняет знак в точке,где она равна 0:
F’(x) = 3x2-8=0,
X=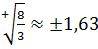 
Так как оба значения лежат вне отрезка [-3;-2], то первая производная не меняет знак. Найдем значение первой производной при x=-3
f’ (-3) = 3 (-3)2 - 8 = 19 > 0
3. Следовательно, на отрезке [-3;-2] первая производная положительная, т.е. функция f(x)= 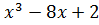монотонно возрастает. Вторая производная f’(x) = 6x на отрезке [-3;-2] всегда отрицательная, т.е. функция f(x)= 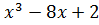выпукла вверх.
Проверим условие f(x0)f”(x0)>0
Для определения начального приближения x0 для корня. Это условие означает, что в точке x0 функция f(x) и ее вторая производная должны быть одного знака. Так как вторая производная всегда отрицательная, то значение функции f(x0) должно быть то же отрицательным.
Значение функции f(x) при x=3 отрицательное: f(-3)=-1.
Поэтому в качестве начального приближения x0 возьмем левый конец отрезка [-3;-2],т.е. x0 = -3.
Задание 3. Найти приближенное значение корня с точностью Ɛ=0,0001.
1) Запишем формулу последовательных приближений (1), полагая в ней f(x)= 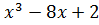, f’(x)=3x2-8,
Тогда
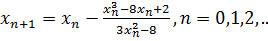
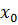= -3
2) Заполните столбец A исходных данных в электронной таблице.
3) Вычислите ячейке B3 первое приближение x1 по формуле (1)
4) Вычислите в ячейке B4 абсолютную погрешность |x-x0|
Так как абсолютная погрешность 0,0526 больше заданной точности Ɛ= 0,0001, то необходимо вычислить второе приближение по формуле.
5) Для вычисления приближения x2 и новой абсолютной погрешности |x2-x1|
Необходимо выделить ячейки B2:B4 и автозаполнением скопировать их в соответствующие ячейки столбца C.
6) Так как абсолютная погрешность |x3-x2|=9,23*10-7
Меньше заданной точности Ɛ= 0,0001, то третье приближение
x3=-2,946 можно принять за приближенное решение уравнения 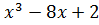на отрезке [-3;-3].
Лабораторная работа 3.
